Câu hỏi:
2 năm trước
Tổng tất cả các giá trị nguyên của m để phương trình \({25^{x + 1}} - {5^{x + 2}} - 4m = 0\) có nghiệm x<1 là
Trả lời bởi giáo viên
Đáp án đúng: c
\({25^{x + 1}} - {5^{x + 2}} - 4m = 0\)\( \Leftrightarrow {\left( {{5^{x + 1}}} \right)^2} - {5.5^{x + 1}} - 4m = 0 \Leftrightarrow 4m = {\left( {{5^{x + 1}}} \right)^2} - {5.5^{x + 1}}\)
Đặt \(t = {5^{x + 1}} \Rightarrow 0 < t < 25\)
Phương trình trên trở thành \(4m = {t^2} - 5t \Leftrightarrow m = \dfrac{{{t^2}}}{4} - \dfrac{5}{4}t = f\left( t \right)\)(1)
Bảng biến thiên của hàm số y=f(t) trên (0;25)
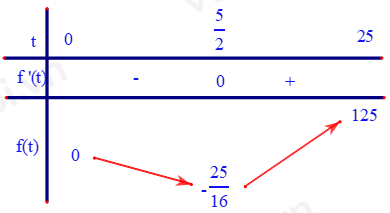
Phương trình (1) có nghiệm trên (0;25) khi và chỉ khi \(\dfrac{{ - 25}}{{16}} \le m < 125 \Leftrightarrow - 1 \le m \le 124\)
Tổng các giá trị của m là:
-1+0+1+2+…+124=7749
Hướng dẫn giải:
- Đặt \(t = {5^{x + 1}} \Rightarrow 0 < t < 25\), đưa về phương trình ẩn t
- Xét hàm số \(f\left( t \right)\)
- Lập bảng biến thiên và tìm điều kiện của m
