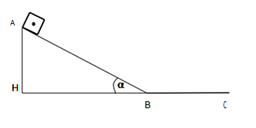
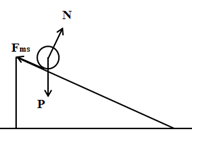
Một lò xo có chiều dài tự nhiên là \(20cm\). Khi lò xo có chiều dài \(24cm\) thì lực đàn hồi của nó bằng \(5N\). Hỏi khi lực đàn hồi của lò xo bằng \(10N\) thì chiều dài của nó bằng bao nhiêu?
Ta có:
\({l_0} = 20cm\)
+ Khi \(l = {l_1} = 24cm\) thì độ dãn của lò xo \(\Delta {l_1} = {l_1} - {l_0} = 24 - 20 = 4cm = 0,04m\)
=> Độ lớn của lực đàn hồi \({F_{d{h_1}}} = 5N = k.\Delta {l_1} \leftrightarrow 5 = k.0,04 \to k = 125N/m\)
+ Gọi \({l_2},\Delta {l_2}\) là chiều dài của lò xo và độ dãn của lò xo khi lực đàn hồi của lò xo là: \({F_{d{h_2}}} = 10N\)
Ta có: \({F_{d{h_2}}} = k\Delta {l_2} \leftrightarrow 10 = 125.\Delta {l_2} \to \Delta {l_2} = 0,08m = 8cm\)
=> Chiều dài của lò xo: \({l_2} = {l_0} + \Delta {l_2} = 20 + 8 = 28cm\)
Phải treo một vật có khối lượng bằng bao nhiêu vào lò xo có độ cứng \(k = 100N/m\) để lò xo dãn ra được \(10cm\)? Lấy \(g = 10m/{s^2}\)
Ta có: Khi treo vật m vào lò xo thì tại vị trí cân bằng thì độ lớn của lực đàn hồi bằng với trọng lượng của vật: \({F_{dh}} = P\)
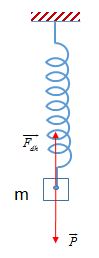
Lực đàn hồi: \({F_{dh}} = k\Delta l = 100.0,1 = 10N\)
Trọng lượng của vật: \(P = mg\)
Ta suy ra, để lò xo giãn \(10cm\) thì khối lượng của vật : \(m = \dfrac{{{F_{dh}}}}{g} = \dfrac{{10}}{{10}} = 1kg\)
Một vật lúc đầu nằm trên một mặt phẳng nhám nằm ngang. Sau khi được truyền một vận tốc đầu, vật chuyển động chậm dần vì:
Ta có, lực ma sát có tác dụng cản trở chuyển động của vật
=> Vật chuyển động chậm dần vì lực ma sát.
Điều gì xảy ra đối với hệ số ma sát giữa 2 mặt tiếp xúc nếu lực pháp tuyến ép hai mặt tiếp xúc tăng lên ?
Mỗi vật, chất xác định có hệ số ma sát nhất định không thay đổi
Một vật trượt trên một mặt phẳng, khi tốc độ của vật tăng thì hệ số ma sát giữa vật và mặt phẳng:
Khi tốc độ của vật tăng thì hệ số ma sát giữa vật và mặt phẳng luôn không đổi
Lò xo nằm ngang có độ cứng \(k = 200N/m\) một đầu gắn cố định, đầu còn lại gắn với \(m\) có khối lượng \(800g\). Độ giãn lớn nhất của lò xo mà tại đó vật vẫn nằm cân bằng là bao nhiêu? Lấy \(g = 10m/{s^2}\) và hệ số ma sát trượt là \(1,2\)
Theo phương ngang vật chịu tác dụng của lực đàn hồi và lực ma sát
Tại vị trí lò xo giãn lớn nhất mà vẫn cân bằng thì khi đó, lực đàn hồi cân bằng với lực ma sát
\(\begin{array}{l}{F_{dh}} = {F_{ms}}\\ \leftrightarrow k\Delta l = \mu N \leftrightarrow k\Delta l = \mu mg\\ \to \Delta l = \dfrac{{\mu mg}}{k} = \dfrac{{1,2.0,8.10}}{{200}} = 0,048m = 4,8cm\end{array}\)
Từ mặt đất ném một vật khối lượng \(5kg\) lên cao theo phương thẳng đứng. Thời gian đạt độ cao cực đại là \({t_1}\) và thời gian trở lại mặt đất là \({t_2}\). Biết \({t_1} = \dfrac{{{t_2}}}{2}\), \(g = 10m/{s^2}\) . Lực cản của không khí (xem như không đổi) có giá trị là:
Chọn chiều dương trùng chiều chuyển động của vật:
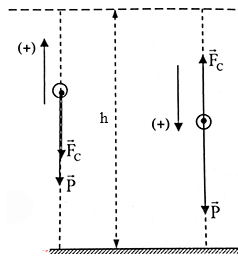
Viết phương trình định luật II – Niuton trong các trường hợp:
+ Khi vật chuyển động đi lên: \( - P - {F_C} = m{a_1} \to {a_1} = - g - \dfrac{{{F_C}}}{m}\)
+ Khi vật chuyển động đi xuống: \(P - {F_C} = m{a_2} \to {a_2} = g - \dfrac{{{F_C}}}{m}\)
Gọi \({v_0}\) là vận tốc lúc ném lên và \(h\) là độ cao cực đại vật đạt được
Ta có khi lên đến độ cao cực đại thì vận tốc của vật \(v = 0\), nên ta có:
\({v^2} - v_0^2 = 2{a_1}h \leftrightarrow - v_0^2 = 2{a_1}h \to {v_0} = \sqrt {2h\left( {g - \dfrac{{{F_c}}}{m}} \right)} \)
=> Thời gian vật đạt độ cao cực đại: \({t_1} = - \dfrac{{{v_0}}}{{{a_1}}} = \dfrac{{2h}}{{{v_0}}}\)
Thời gian khi vật trở lại mặt đất: \({t_2} = \sqrt {\dfrac{{2h}}{{{a_2}}}} \)
+ Mặt khác, theo đầu bài ta có: \({t_1} = \dfrac{{{t_2}}}{2} \leftrightarrow \dfrac{{2h}}{{{v_0}}} = \dfrac{{\sqrt {\dfrac{{2h}}{{{a_2}}}} }}{2}\)
\(\begin{array}{l} \leftrightarrow \dfrac{{2h}}{{\sqrt {2h\left( {g + \dfrac{{{F_C}}}{m}} \right)} }} = \dfrac{1}{2}\sqrt {\dfrac{{2h}}{{g - \dfrac{{{F_C}}}{m}}}} \\ \leftrightarrow 4h\sqrt {g - \dfrac{{{F_C}}}{m}} = 2h\sqrt {g + \dfrac{{{F_C}}}{m}} \\ \leftrightarrow 4\left( {g - \dfrac{{{F_C}}}{m}} \right) = g + \dfrac{{{F_C}}}{m}\\ \to {F_C} = \dfrac{3}{5}mg = \dfrac{3}{5}5.10 = 30N\end{array}\)
Vật trượt từ đỉnh mặt phẳng nghiêng nhãn dài \(l = 10m\), góc nghiêng \(\alpha = {30^0}\) . Hỏi vật tiếp tục chuyển động trên mặt phẳng ngang bao lâu khi xuống hết mặt phẳng nghiêng, biết hệ số ma sát với mặt phẳng ngang là \(\mu = 0,1\).
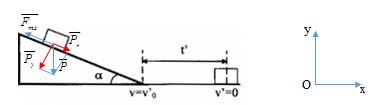
+ Gắn hệ trục tọa độ như hình vẽ
+ Viết phương trình định luật II – Niuton cho vật ta được:
\(\overrightarrow P + \overrightarrow {{F_{ms}}} = m\overrightarrow a \) (1)
+ Chiếu (1) lên các phương ta được:
Ox: \({P_x} - {F_{ms}} = ma \to a = \dfrac{{{P_x} - {F_{ms}}}}{m} = \dfrac{{P\sin \alpha - \mu P\cos \alpha }}{m} = g\sin \alpha - \mu g\cos \alpha \)
+ Vì mặt phẳng nghiêng nhẵn nên hệ số ma sát bằng \(0\), do đó: \(a = g.\sin \alpha = 10.\sin {30^0} = 5m/{s^2}\)
+ Vận tốc của vật ở cuối mặt phẳng nghiêng là: \(v = \sqrt {2al} = \sqrt {2.5.10} = 10m/s\)
+ Gia tốc của vật trên mặt phẳng ngang là: \(a' = - \dfrac{{{F_{ms}}}}{m} = - \dfrac{{\mu mg}}{m} = - \mu g = - 0,1.10 = - 1m/{s^2}\)
+ Thời gian vật đi trên mặt phẳng ngang là: \(t' = \dfrac{{v' - v{'_0}}}{{a'}} = \dfrac{{0 - v}}{{a'}}\) (do vật dừng lại nên \(v' = 0\) )
Ta suy ra: \(t' = \dfrac{{ - v}}{{a'}} = \dfrac{{ - 10}}{{ - 1}} = 10s\)
Một vật khối lượng \(m\) đang chuyển động tròn đều trên một quỹ đạo bán kính \(r\) với tốc độ góc \(\omega \). Lực hướng tâm tác dụng vào vật là:
Lực hướng tâm: \({F_{ht}} = m{a_{ht}} = \dfrac{{m{v^2}}}{r} = m.{\omega ^2}r\)
Một vật nhỏ khối lượng \(350g\) chuyển động tròn đều trên quỹ đạo bán kính \(1,25{\rm{ }}m\) với tốc độ dài là \(2,5m/s\). Độ lớn lực hướng tâm gây ra chuyển động tròn của vật là:
Ta có, lực hướng tâm: \({F_{ht}} = m{a_{ht}} = m\frac{{{v^2}}}{r}\)
Thay số ta được: \({F_{ht}} = 0,35\frac{{{{2,5}^2}}}{{1,25}} = 1,75N\)
Một vật nhỏ khối lượng \(250{\rm{ }}g\) chuyển động tròn đều trên quỹ đạo bán kính \(1,2{\rm{ }}m\). Biết trong \(2\) phút vật quay được \(120\) vòng. Độ lớn lực hướng tâm gây ra chuyển động tròn của vật là:
+ Tần số: \(f = \frac{{120}}{{60.2}} = 1\left( {H{\rm{z}}} \right)\)
+ Tốc độ góc: \(\omega = 2\pi f = 2\pi .1 = 2\pi \left( {ra{\rm{d}}/s} \right)\)
+ Ta có, lực hướng tâm: \({F_{ht}} = m{\omega ^2}r = 0,25.{\left( {2\pi } \right)^2}.1,2 \approx 11,84N\)
Từ độ cao \(20m\) ném vật theo phương ngang xuống đất biết rằng sau \(1\) giây kể từ lúc ném thì véc-tơ vận tốc hợp với phương ngang góc \({45^0}\) . Lấy \(g = 10m/{s^2}\)
Vận tốc lúc ném có giá trị là:
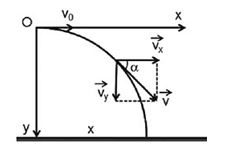
+ Gắn hệ trục tọa độ như hình vẽ
+ Ta có phương trình vận tốc của vật: \(\left\{ \begin{array}{l}{v_x} = {v_0}\\{v_y} = gt\end{array} \right.\)
Biết sau \(1\) giây kể từ lúc ném thì véc-tơ vận tốc hợp với phương ngang góc \({45^0}\)
Từ hình ta có: \(\tan \alpha = \dfrac{{{v_y}}}{{{v_x}}} \leftrightarrow \tan {45^0} = \dfrac{{g.1}}{{{v_0}}} \to {v_0} = g = 10m/s\)
Từ độ cao \(20m\) ném vật theo phương ngang xuống đất biết rằng sau \(1\) giây kể từ lúc ném thì véc-tơ vận tốc hợp với phương ngang góc \({45^0}\) . Lấy \(g = 10m/{s^2}\)
Vị trí vật chạm đất theo phương ngang so với vị trí ban đầu là:
Vị trí vật chạm đất theo phương ngang so với vị trí ban đầu chính là tầm xa của vật:
\(x = L = {v_0}\sqrt {\dfrac{{2h}}{g}} = 10\sqrt {\dfrac{{2.20}}{{10}}} = 20m\)
Vật được thả trượt trên mặt phẳng nghiêng dài AB = 2,5m, góc nghiêng α = 300 như hình vẽ, có hệ số ma sát µ = 0,2. Cho g = 10m/s2. Tính vận tốc vật đạt được ở chân mặt phẳng nghiêng và thời gian vật đi hết mặt phẳng nghiêng
Áp dụng định luật 2 Niu tơn ta có:
\(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{{{F}_{ms}}}=m\overrightarrow{a}\)
Chiếu lên Oy ta được: N = Py = mgcosα
Chiếu lên Ox ta được:
Px – Fms = ma
mgsinα - µmgcosα = ma
a = gsinα - µgcosα = 3,27m/s2
v0 = 0, S = 2,5m
Thời gian đi hết mặt phẳng nghiêng : S = 0,5at2 =2,5m --> t = 1,24s
Vận tốc ở chân mặt phẳng nghiêng: v = at = 4,05m/s
Một quả cầu được ném theo phương ngang từ độ cao 80 m. Sau khi chuyển động 3s, vận tốc của quả cầu hợp với phương ngang góc 450. Vận tốc ban đầu của quả cầu và vận tốc chạm đất của quả cầu là:
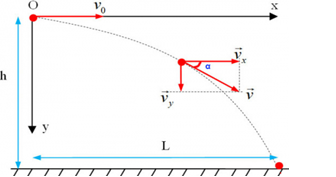
+ Góc hợp bởi vecto vận tốc của vật và phương ngang là:\(\alpha = \left( {\overrightarrow v ;\overrightarrow {{v_x}} } \right) = {45^0}\)
Ta có: \(\tan \alpha = \dfrac{{{v_y}}}{{{v_x}}} = \dfrac{{gt}}{{{v_0}}} \Leftrightarrow \tan 45 = \dfrac{{10.3}}{{{v_0}}} \Rightarrow {v_0} = 30m/s\)
+ Vận tốc chạm đất: \({v_{cd}} = \sqrt {v_0^2 + 2gh} = \sqrt {{{30}^2} + 2.10.80} = 50m/s\)
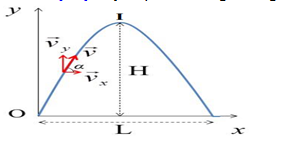
Hãy chọn câu đúng. Trong hình vẽ, gia tốc của vật tại điểm đỉnh I:
Tại mọi điểm trên quỹ đạo, gia tốc của vật luôn là vectơ \(\overrightarrow g \) vì trong suốt thời gian chuyển động, vật chỉ chịu tác dụng của trọng lực \(\overrightarrow P \) có chiều hướng thẳng đứng xuống dưới.
Một xe trượt không vận tốc đầu từ đỉnh mặt phẳng nghiêng góc α = 30°. Chiều dài mặt phẳng nghiêng là l = 1m. Lấy g = 10m/s2 và hệ số ma sát μ = 0,3464. Tính gia tốc chuyển động của vật.
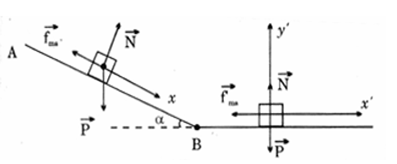
- Các lực tác dụng vào vật: Trọng lực \(\overrightarrow P \); lực ma sát \(\overrightarrow {{f_{ms}}} \); phản lực \(\overrightarrow N \) của mặt phẳng nghiêng.
- Phương trình định luật II Niu-tơn dưới dạng véc tơ:
\(\overrightarrow {{F_{ms}}} + \overrightarrow P + \overrightarrow N = m.\overrightarrow a \) (*)
- Chiếu (*) lên trục Ox và Oy ta được: \(\left\{ \begin{array}{l}P.sin\alpha - {f_{ms}} = m{a_x}\\ - {\rm{ }}Pcos\alpha + N = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}N = P.\cos \alpha \\P.sin\alpha - {f_{ms}} = m{a_x}\,\,\,\left( 2 \right)\end{array} \right.\)
Lực ma sát : \({f_{ms}} = \mu .N = \mu .P\cos \alpha = \mu mg.\cos \alpha \,\,\,\,\left( 3 \right)\)
Từ (2) và (3) ta có:
\(\begin{array}{l}m{a_x} = P\sin \alpha - {f_{ms}} = mg.\sin \alpha - \mu mg.\cos \alpha \\ \Rightarrow {a_x} = g.\left( {\sin \alpha - \mu .\cos \alpha } \right) = 10.\left( {\sin 30 - 0,3464.\cos 30} \right) = 2m/{s^2}\end{array}\)
