Câu hỏi:
2 năm trước
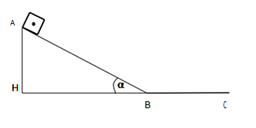
Vật được thả trượt trên mặt phẳng nghiêng dài AB = 2,5m, góc nghiêng α = 300 như hình vẽ, có hệ số ma sát µ = 0,2. Cho g = 10m/s2. Tính vận tốc vật đạt được ở chân mặt phẳng nghiêng và thời gian vật đi hết mặt phẳng nghiêng
Trả lời bởi giáo viên
Đáp án đúng: d
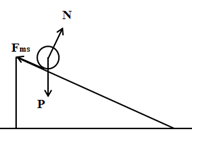
Áp dụng định luật 2 Niu tơn ta có:
\(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{{{F}_{ms}}}=m\overrightarrow{a}\)
Chiếu lên Oy ta được: N = Py = mgcosα
Chiếu lên Ox ta được:
Px – Fms = ma
mgsinα - µmgcosα = ma
a = gsinα - µgcosα = 3,27m/s2
v0 = 0, S = 2,5m
Thời gian đi hết mặt phẳng nghiêng : S = 0,5at2 =2,5m --> t = 1,24s
Vận tốc ở chân mặt phẳng nghiêng: v = at = 4,05m/s
Hướng dẫn giải:
- Áp dụng định luật 2 Niu tơn
- Lực ma sát Fms = µN
- Công thức tính quãng đường S = vot + 0,5at2
- Công thức tính vận tốc v = v0 + at
