Từ mặt đất ném một vật khối lượng \(5kg\) lên cao theo phương thẳng đứng. Thời gian đạt độ cao cực đại là \({t_1}\) và thời gian trở lại mặt đất là \({t_2}\). Biết \({t_1} = \dfrac{{{t_2}}}{2}\), \(g = 10m/{s^2}\) . Lực cản của không khí (xem như không đổi) có giá trị là:

Chọn chiều dương trùng chiều chuyển động của vật:

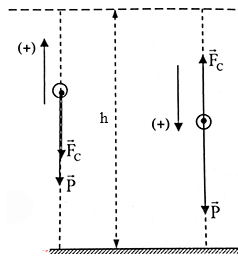
Viết phương trình định luật II – Niuton trong các trường hợp:

+ Khi vật chuyển động đi lên: \( - P - {F_C} = m{a_1} \to {a_1} =  - g - \dfrac{{{F_C}}}{m}\)

+ Khi vật chuyển động đi xuống: \(P - {F_C} = m{a_2} \to {a_2} = g - \dfrac{{{F_C}}}{m}\)

Gọi \({v_0}\) là vận tốc lúc ném lên và \(h\) là độ cao cực đại vật đạt được

Ta có khi lên đến độ cao cực đại thì vận tốc của vật \(v = 0\), nên ta có:

\({v^2} - v_0^2 = 2{a_1}h \leftrightarrow  - v_0^2 = 2{a_1}h \to {v_0} = \sqrt {2h\left( {g - \dfrac{{{F_c}}}{m}} \right)} \)  

=> Thời gian vật đạt độ cao cực đại: \({t_1} =  - \dfrac{{{v_0}}}{{{a_1}}} = \dfrac{{2h}}{{{v_0}}}\)

Thời gian khi vật trở lại mặt đất: \({t_2} = \sqrt {\dfrac{{2h}}{{{a_2}}}} \)

+ Mặt khác, theo đầu bài ta có: \({t_1} = \dfrac{{{t_2}}}{2} \leftrightarrow \dfrac{{2h}}{{{v_0}}} = \dfrac{{\sqrt {\dfrac{{2h}}{{{a_2}}}} }}{2}\)

\(\begin{array}{l} \leftrightarrow \dfrac{{2h}}{{\sqrt {2h\left( {g + \dfrac{{{F_C}}}{m}} \right)} }} = \dfrac{1}{2}\sqrt {\dfrac{{2h}}{{g - \dfrac{{{F_C}}}{m}}}} \\ \leftrightarrow 4h\sqrt {g - \dfrac{{{F_C}}}{m}}  = 2h\sqrt {g + \dfrac{{{F_C}}}{m}} \\ \leftrightarrow 4\left( {g - \dfrac{{{F_C}}}{m}} \right) = g + \dfrac{{{F_C}}}{m}\\ \to {F_C} = \dfrac{3}{5}mg = \dfrac{3}{5}5.10 = 30N\end{array}\)