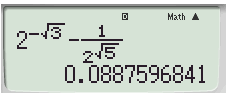Lũy thừa (số mũ vô tỉ)

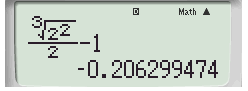
Đáp án A: Vì \(\sqrt 3  > 1\) và \(\sqrt 3  > \sqrt 2 \) nên \({\left( {\sqrt 3 } \right)^{\sqrt 3 }} > {\left( {\sqrt 3 } \right)^{\sqrt 2 }}\) hay A đúng.

Đáp án B: Vì \(\dfrac{1}{{\sqrt 3 }} < 1\) và \(\sqrt 3  < \sqrt 5 \) nên \({\left( {\dfrac{1}{{\sqrt 3 }}} \right)^{\sqrt 3 }} > {\left( {\dfrac{1}{{\sqrt 3 }}} \right)^{\sqrt 5 }}\) hay B sai.

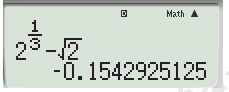
Đáp án C: \({\left( {\dfrac{1}{2}} \right)^{ - \sqrt 3 }} = {2^{\sqrt 3 }}\), \({\left( {\dfrac{1}{3}} \right)^{ - \sqrt 3 }} = {3^{\sqrt 3 }}\). Vì \(2 < 3\) nên \({2^{\sqrt 3 }} < {3^{\sqrt 3 }}\) hay \({\left( {\dfrac{1}{2}} \right)^{ - \sqrt 3 }} < {\left( {\dfrac{1}{3}} \right)^{ - \sqrt 3 }}\) nên C sai.

Đáp án D: Vì \(\dfrac{2}{3} > \dfrac{1}{3}\) nên \({\left( {\dfrac{2}{3}} \right)^{\sqrt 3 }} > {\left( {\dfrac{1}{3}} \right)^{\sqrt 3 }}\) hay D sai.

Vì \(\left\{ \begin{array}{l}\dfrac{1}{2} > \dfrac{1}{6}\\{a^{\dfrac{1}{2}}} > {a^{\dfrac{1}{6}}}\end{array} \right. \Rightarrow a > 1\) và \(\left\{ \begin{array}{l}\sqrt 2  < \sqrt 3 \\{b^{\sqrt 2 }} > {b^{\sqrt 3 }}\end{array} \right. \Rightarrow 0 < b < 1\)

Do \(\sqrt 3  < \sqrt 7 \) và số mũ không nguyên \( \Rightarrow {a^{\sqrt 3 }} > {a^{\sqrt 7 }}\) $ \Leftrightarrow 0 < a < 1$.

Do \( - \dfrac{2}{3} <  - \dfrac{1}{3}\) và số mũ không nguyên nên \({(a - 1)^{ - \dfrac{2}{3}}} < {(a - 1)^{ - \dfrac{1}{3}}}\) khi \(a - 1 > 1 \Leftrightarrow a > 2\).

Do \( - 3 <  - 1\) và số mũ nguyên âm nên ${(2a + 1)^{ - 3}} > {(2a + 1)^{ - 1}}$ khi $\left[ \begin{array}{l}0 < 2a + 1 < 1\\2a + 1 <  - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - \dfrac{1}{2} < a < 0\\a <  - 1\end{array} \right.$.

Do \( - \dfrac{1}{3} >  - \dfrac{1}{2}\) và số mũ không nguyên \( \Rightarrow \left( {1 - a} \right){\,^{ - \dfrac{1}{3}}} > \left( {1 - a} \right){\,^{ - \dfrac{1}{2}}}\) $ \Leftrightarrow 1-a > 1$ $ \Leftrightarrow a<0$.

Do \(\dfrac{3}{4} < 2\) và có số mũ không nguyên \( \Rightarrow \left( {2 - a} \right){\,^{\dfrac{3}{4}}} > {\left( {2 - a} \right)^2}\) $ \Leftrightarrow 0 < 2 - a < 1 \Leftrightarrow  - 2 <  - a <  - 1 \Leftrightarrow 2 > a > 1$

Ta có: \({{9}^{x}}+{{9}^{-x}}=23\)

\(\begin{array}{l}
\Leftrightarrow {9^x} + {9^{ - x}} + 2 = 25\\
\Leftrightarrow {\left( {{3^x}} \right)^2} + {\left( {{3^{ - x}}} \right)^2} + {2.3^x}{.3^{ - x}} = 25
\end{array}\)

\(\Leftrightarrow {{\left( {{3}^{x}}+{{3}^{-x}} \right)}^{2}}=25\)

\(\Leftrightarrow {{3}^{x}}+{{3}^{-x}}=5\) vì \({{3}^{x}}+{{3}^{-x}}>0,\forall x\in R\)

\(\Rightarrow A=\frac{5+{{3}^{x}}+{{3}^{-x}}}{1-{{3}^{x}}-{{3}^{-x}}}=\frac{5+5}{1-5}=\frac{-5}{2}=\frac{a}{b}.\)

Vậy \(ab=-10.\)

Ta chọn a = 2 sau đó chuyển vế phải sang nếu kết quả nào ra số dương thì đó là kết quả đúng.

Đáp án A: (sai)

Đáp án B

Nên đáp án B đúng.

Đáp án C (sai)

Đáp án D.

\(\frac{1}{{{a^{2016}}}} = {a^{ - 2016}};\frac{1}{{{a^{2017}}}} = {a^{ - 2017}}\)

Do a > 1 mà \( - 2016 >  - 2017 \Rightarrow {a^{ - 2016}} > {a^{ - 2017}}\)

Nên D sai.

\(\begin{array}{l}
f(x) = \dfrac{{{{2018}^x}}}{{{{2018}^x} + \sqrt {2018} }}\\
f(1 - x) = \dfrac{{{{2018}^{1 - x}}}}{{{{2018}^{1 - x}} + \sqrt {2018} }} = \dfrac{{\dfrac{{2018}}{{{{2018}^x}}}}}{{\dfrac{{2018}}{{{{2018}^x}}} + \sqrt {2018} }} = \dfrac{{2018}}{{2018 + \sqrt {2018} {{.2018}^x}}} = \dfrac{{\sqrt {2018} }}{{\sqrt {2018} + {{2018}^x}}}\\
f(x) + f(1 - x) = \dfrac{{{{2018}^x}}}{{{{2018}^x} + \sqrt {2018} }} + \dfrac{{\sqrt {2018} }}{{\sqrt {2018} + {{2018}^x}}} = 1
\end{array}\)

Ta có :

\(\begin{array}{l}
S = f\left( {\dfrac{1}{{2017}}} \right) + f\left( {\dfrac{2}{{2017}}} \right) + ... + f\left( {\dfrac{{2016}}{{2017}}} \right)\\
= \left[ {f\left( {\dfrac{1}{{2017}}} \right) + f\left( {\dfrac{{2016}}{{2017}}} \right)} \right] + \left[ {f\left( {\dfrac{2}{{2017}}} \right) + f\left( {\dfrac{{2015}}{{2017}}} \right)} \right] + ... + \left[ {f\left( {\dfrac{{1008}}{{2017}}} \right) + f\left( {\dfrac{{1009}}{{2017}}} \right)} \right]\\
= \left[ {f\left( {\dfrac{1}{{2017}}} \right) + f\left( {1 - \dfrac{1}{{2017}}} \right)} \right] + \left[ {f\left( {\dfrac{2}{{2017}}} \right) + f\left( {1 - \dfrac{2}{{2017}}} \right)} \right] + ... + \left[ {f\left( {\dfrac{{1008}}{{2017}}} \right) + f\left( {1 - \dfrac{{1008}}{{2017}}} \right)} \right]
\end{array}\)

\(= 1+ 1+ ... +1\) (có: 1008 số 1)

= 1.1008 = 1008.

Ta có \(f\left( x \right)=\frac{{{4}^{x}}}{{{4}^{x}}+2}\Rightarrow f\left( 1-x \right)=\frac{{{4}^{1\,-\,x}}}{{{4}^{1\,-\,x}}+2}\)

\(\begin{align} & \Rightarrow f\left( x \right)+f\left( 1-x \right)=\frac{{{4}^{x}}}{{{4}^{x}}+2}+\frac{{{4}^{1-x}}}{{{4}^{1-x}}+2}=\frac{{{4}^{x}}}{{{4}^{x}}+2}+\frac{4}{4+{{2.4}^{x}}} \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{{4}^{x}}}{{{4}^{x}}+2}+\frac{2}{{{4}^{x}}+2}=1. \\\end{align}\)

Khi đó \(f\left( \frac{1}{2019} \right)+f\left( \frac{2018}{2019} \right)=1;\) \(f\left( \frac{2}{2019} \right)+f\left( \frac{2017}{2019} \right)=1;\) … và \(f\left( 1 \right)=\frac{4}{6}.\)

Vậy \(S=f\left( \frac{1}{2019} \right)+f\left( \frac{2}{2019} \right)+\,\,...\,\,+f\left( \frac{2018}{2019} \right)+f\left( 1 \right)=\frac{2018}{2}.1+\frac{4}{6}=\frac{3029}{3}.\)

Ta có \(2017!.{{\left( 1+\frac{1}{1} \right)}^{1}}{{\left( 1+\frac{1}{2} \right)}^{2}}...{{\left( 1+\frac{1}{2017} \right)}^{2017}}\) \(=2017!{{.2}^{1}}.{{\left( \frac{3}{2} \right)}^{2}}.{{\left( \frac{4}{3} \right)}^{3}}...{{\left( \frac{2017}{2016} \right)}^{2016}}.{{\left( \frac{2018}{2017} \right)}^{2017}}\)

\(=2017!.\frac{1}{1}.\frac{1}{2}.\frac{1}{3}...\frac{1}{2016}.\frac{{{2018}^{2017}}}{2017}\) \(={{2018}^{2017}}={{a}^{b}}\) \(\Rightarrow \left( a;b \right)=\left( 2018;2017 \right).\)

\(P = {a^{ - 2\sqrt 2 }}{\left( {\frac{1}{{{a^{ - \sqrt 2  - 1}}}}} \right)^{\sqrt 2  + 1}}\)\( = {a^{ - 2\sqrt 2 }}{\left( {{a^{\sqrt 2  + 1}}} \right)^{\sqrt 2  + 1}}\)\( = {a^{ - 2\sqrt 2 }}{a^{{{\left( {\sqrt 2  + 1} \right)}^2}}}\) \( = {a^{ - 2\sqrt 2  + {{\left( {\sqrt 2  + 1} \right)}^2}}}\) \( = {a^{ - 2\sqrt 2  + 3 + 2\sqrt 2 }}\) \( = {a^3}\).

Ta có: \({\left( {{a^\alpha }} \right)^\beta } = {a^{\alpha .\beta }}\) nên A sai.

\(Q = \dfrac{{{{\left( {{b^{\sqrt 2  - 1}}} \right)}^{\sqrt 2  + 1}}.\sqrt[3]{{{b^2}}}}}{{{b^{\dfrac{1}{6}}}}}\)    \(\left( {b > 0} \right)\)

\( \Leftrightarrow Q = \dfrac{{{b^{\left( {\sqrt 2  - 1} \right).\left( {\sqrt 2  + 1} \right)}}.{b^{\dfrac{2}{3}}}}}{{{b^{\dfrac{1}{6}}}}} = \dfrac{{{b^{2 - 1}}.{b^{\dfrac{2}{3}}}}}{{{b^{\dfrac{1}{6}}}}} = \dfrac{{b.{b^{\dfrac{2}{3}}}}}{{{b^{\dfrac{1}{6}}}}} = {b^{\dfrac{3}{2}}}\).

Lũy thừa với số mũ không nguyên thì cơ số phải dương nên $a > 0$.

- Vì $n \in {N^*}$ nên ${a^n},{b^n}$ đều có nghĩa (A, B đúng).

- Vì $\alpha  \notin Z,a > 0$ nên ${a^\alpha }$ có nghĩa (C đúng).

- Vì $\alpha  \notin Z,b < 0$ nên ${b^\alpha }$ không có nghĩa (D sai).

Ta có: ${\left( {{2^x}} \right)^y} = {2^{xy}}$ nên A sai.

$\dfrac{{{2^x}}}{{{2^y}}} = {2^{x - y}}$ nên B sai.

${2^x}{.2^y} = {2^{x + y}}$ nên C đúng.

${\left( {\dfrac{2}{3}} \right)^x} = \dfrac{{{2^x}}}{{{3^x}}}$ nên D sai.

${2^{\sqrt x }} \ne {x^{\sqrt 2 }}$ nên A sai.

${3^{\sqrt {xy} }} = {3^{\sqrt x .\sqrt y }} = {\left( {{3^{\sqrt x }}} \right)^{\sqrt y }}$ nên B đúng.

$\dfrac{{{3^{\sqrt[3]{x}}}}}{{{3^{\sqrt[3]{y}}}}} = {3^{\sqrt[3]{x} - \sqrt[3]{y}}} \ne {3^{\sqrt[3]{{x - y}}}}$ nên C sai.

${x^{\sqrt 3 }} \ne {y^{\sqrt 3 }}$ nếu $x \ne y$  nên D sai.

\({\left( {\dfrac{1}{{16}}} \right)^{ - 0,75}} + {\left( {\dfrac{1}{8}} \right)^{ - \frac{4}{3}}} = {16^{0,75}} + {8^{\frac{4}{3}}} = {\left( {{2^4}} \right)^{\frac{3}{4}}} + {\left( {{2^3}} \right)^{\frac{4}{3}}} = {2^3} + {2^4} = 24\).