Hàm số mũ

Vì \({\left( {\dfrac{e}{2}} \right)^x}\) và \( - {\left( {\dfrac{e}{2}} \right)^x}\) đối nhau nên đồ thị hai hàm số đó đối xứng nhau qua \(Ox\).

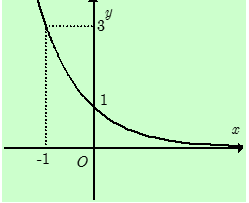
Dựa vào hình dáng đồ thị từ trái sang phải ta thấy: \(x\) tăng nhưng \(y\) giảm. 

Suy ra hàm số tương ứng của đồ thị là hàm nghịch biến. Loại A, C.

Đồ thị hàm số đi qua điểm có tọa độ \(\left( { - 1;3} \right)\) nên chỉ có D thỏa mãn.

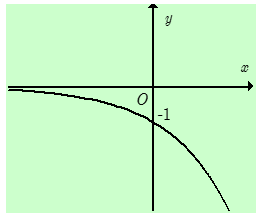
Đồ thị nằm phía dưới trục hoành. Loại B, C.

Lấy đối xứng đồ thị qua trục hoành ta được đồ thị của một hàm số đồng biến.

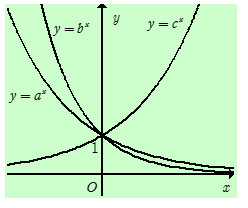
Ta thấy hàm $y = {c^x}$ có đồ thị từ trái sang phải theo hướng đi lên nên là hàm đồng biến \( \Rightarrow c > 1.\) Còn hàm số $y = {a^x}$ và $y = {b^x}$ là những hàm nghịch biến \( \Rightarrow a,{\rm{ }}b < 1.\) Từ đó loại được các đáp án A, D.

Từ đồ thị hàm số ta thấy tại cùng một giá trị ${x_0} < 0$ thì đồ thị hàm số $y = {b^x}$ nằm trên đồ thị hàm số $y = {a^x}$ hay \(\left\{ \begin{array}{l}x < 0\\{b^x} > {a^x}\end{array} \right. \Rightarrow b < a\).

Ví dụ \(\left\{ \begin{array}{l}x =  - 1\\{b^{ - 1}} > {a^{ - 1}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 1\\\dfrac{1}{b} > \dfrac{1}{a}\end{array} \right. \to b < a.\)

Vậy $c > a > b.$

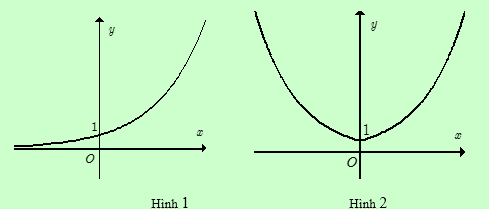
Từ đồ thị ta thấy: Đồ thị Hình 2 có được là lấy đối xứng đồ thị Hình 1 (phần \(x \ge 0\)) qua trục \(Oy\). Do đó hàm số của đồ thị Hình 2 là hàm số chẵn.

Ngoài ra, đồ thị hàm số ở hình 2 nằm hoàn toàn phía trên trục hoành nên loại B, D.

Hàm số ở đáp án A \(y = \left| {{{\left( {\sqrt 2 } \right)}^x}} \right| = {\left( {\sqrt 2 } \right)^x}\) vẫn là đồ thị hình 1 nên loại.

Áp dụng công thức \(\left( {{a^x}} \right)' = {a^x}.\ln a\), ta có $y' = \left( {{{13}^x}} \right)' = {13^x}.\ln 13$.

Áp dụng công thức \(\left( {{a^u}} \right)' = u'.{a^u}.\ln a\), ta có $y' = \left( {{x^2}} \right)'{.2^{{x^2}}}.\ln 2$

$ = 2x{.2^{{x^2}}}.\ln 2 = x{.2^{1 + {x^2}}}.\ln 2$.

Ta có $y' = \left( {\sqrt {2x} } \right)'.{e^{\sqrt {2x} }} = \dfrac{2}{{2\sqrt {2x} }}.{e^{\sqrt {2x} }} = \dfrac{{{e^{\sqrt {2x} }}}}{{\sqrt {2x} }}.$

Ta có $y' = \left( {\dfrac{{x + 1}}{{{4^x}}}} \right)' = \dfrac{{\left( {x + 1} \right)'{{.4}^x} - \left( {x + 1} \right).\left( {{4^x}} \right)'}}{{{{\left( {{4^x}} \right)}^2}}}$

$ = \dfrac{{{4^x} - \left( {x + 1} \right){{.4}^x}.\ln 4}}{{{{\left( {{4^x}} \right)}^2}}} = \dfrac{{1 - \left( {x + 1} \right).\ln 4}}{{{4^x}}} = \dfrac{{1 - 2\left( {x + 1} \right)\ln 2}}{{{2^{2x}}}}$.

Ta có $\left\{ \begin{array}{l}\left( {{e^{ - x}}} \right)' =  - {e^{ - x}}\\{e^{\cos x}} = \left( {\cos x} \right)'{e^{\cos x}} =  - \sin x.{e^{\cos x}}\end{array} \right.$$ \Rightarrow y' =  - 3{e^{ - x}} - 2017.\sin x.{e^{\cos x}}$

Ta có \(f'\left( x \right) = {\left( {{x^2} + 1} \right)^/}{.2^{{x^2} + 1}}.\ln 2 = 2x.\ln {2.2^{{x^2} + 1}}.\)

Vậy \(T = {2^{ - {x^2} - 1}}.2x\ln {2.2^{{x^2} + 1}} - 2x\ln 2 + 2\) \( = 2x\ln 2 - 2x\ln 2 + 2 = 2\)

Viết lại $y = {x^x} = {e^{x\ln x}}$.

Suy ra $y' = \left( {x\ln x} \right)'{e^{x\ln x}} = \left( {\ln x + 1} \right).{e^{x\ln x}} = \left( {\ln x + 1} \right){x^x}$.

Ta có $\left\{ \begin{array}{l}y' =  - \sin x.{e^{\cos x}}\\y'' = {\sin ^2}x.{e^{\cos x}} - \cos x.{e^{\cos x}}\end{array} \right..$

Thay lần lượt vào các đáp án thì ta được đáp án B đúng.

Thật vậy:

Ta có $y'.\sin x + y.\cos x + y''$

$ =  - \sin x.{e^{\cos x}}.\sin x + {e^{\cos x}}.\cos x + {\sin ^2}x.{e^{\cos x}} - \cos x.{e^{\cos x}} = 0$.

Ta có $y' = {e^{ - x}} - x.{e^{ - x}} = \left( {1 - x} \right){e^{ - x}}$

Nhân hai vế cho \(x\), ta được $x.y' = x.\left( {1 - x} \right).{e^{ - x}} = \left( {1 - x} \right).y$.

Ta có $y' =  - {e^{ - x}}.\sin x + {e^{ - x}}.\cos x = {e^{ - x}}\left( {\cos x - \sin x} \right).$

Lại có $y'' =  - {e^{ - x}}\left( {\cos x - \sin x} \right) + {e^{ - x}}\left( { - \sin x - \cos x} \right) =  - 2{e^{ - x}}.\cos x$

Ta thấy $y'' + 2y' + 2y =  - 2{e^{ - x}}.\cos x + 2{e^{ - x}}\left( {\cos x - \sin x} \right) + 2{e^{ - x}}.\sin x = 0$.

Ta có $y' = {e^{ - \frac{{{x^2}}}{2}}} + x.\left( { - x{e^{ - \frac{{{x^2}}}{2}}}} \right) $ $= {e^{ - \frac{{{x^2}}}{2}}} - {x^2}{e^{ - \frac{{{x^2}}}{2}}} = \left( {1 - {x^2}} \right){e^{ - \frac{{{x^2}}}{2}}}$.

Nhân hai vế cho \(x\), ta được $x.y' = x\left( {1 - {x^2}} \right){e^{ - \frac{{{x^2}}}{2}}} = \left( {1 - {x^2}} \right)y$.

Ta có \(\mathop {\lim }\limits_{x \to 0} \dfrac{{{e^{ax}} - 1}}{{\sin bx}} = \mathop {\lim }\limits_{x \to 0} \left( {\dfrac{{{e^{ax}} - 1}}{{ax}}.\dfrac{{bx}}{{\sin bx}}.\dfrac{a}{b}} \right) = 1.1.\dfrac{a}{b} = \dfrac{a}{b}\)

Vậy để \(\mathop {\lim }\limits_{x \to 0} \dfrac{{{e^{ax}} - 1}}{{\sin bx}} = \dfrac{5}{3}\) thì \(\dfrac{a}{b} = \dfrac{5}{3}\).

Vì \(a,b > 0\) và nguyên tố cùng nhau nên $a = 5,b = 3$. Do đó \(ab = 5.3 = 15\).

Ta có \(\dfrac{{\sqrt 3 }}{3} < \dfrac{{\sqrt 2 }}{2}\), mà \({a^{\frac{{\sqrt 3 }}{3}}} > {a^{\frac{{\sqrt 2 }}{2}}}\).

Suy ra hàm đặc trưng \(y = {a^x}\) nghịch biến nên \(0 < a < 1\).

Vì \(\dfrac{3}{4} < \dfrac{4}{5}\) và \({\log _b}\dfrac{3}{4} < {\log _b}\dfrac{4}{5}\) nên \(b > 1\).

Vậy \(0 < a < 1\) và \(b > 1\) hay \(0 < a < 1 < b\).

Vì \( - 5 < 0\) nên \({\left( { - 5} \right)^x}\) không tồn tại. Do đó 1) sai.

Vì cơ số \(\pi  > 1\) nên từ ${\pi ^\alpha } < {\pi ^{2\alpha }} \Rightarrow \alpha  < 2\alpha  \Leftrightarrow 0 < \alpha $. Do đó 2) sai.

Hàm số $y = {a^x}$ xác định với mọi \(x\). Do đó 3) đúng.

Vì ${a^x} > 0,{\rm{ }}\forall x \in \mathbb{R}$và\(\mathop {\lim }\limits_{x \to  + \infty } {a^x} =  + \infty \) nên hàm $y = {a^x}$ có TGT là $\left( {0; + \infty } \right)$. Do đó 4) đúng.

Vậy có 3) và 4) đúng.

Hàm số xác định và liên tục trên \(\mathbb{R}.\)

Ta có $y' = {e^{ - x}} + x.\left( { - {e^{ - x}}} \right) = {e^{ - x}}\left( {1 - x} \right)$$ \Rightarrow y' = 0 \Leftrightarrow 1 - x = 0 \Leftrightarrow x = 1$

Với \(x > 1\) thì \(y' < 0\) và với \(x < 1\) thì \(y' > 0\) nên \(y'\) đổi dấu từ dương sang âm qua điểm \(x = 1\).

Vậy hàm số đạt cực đại tại $x = 1$.