Câu hỏi:
2 năm trước
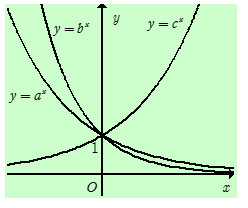
Cho $a,{\rm{ }}b,{\rm{ }}c$ là các số thực dương khác $1$. Hình vẽ bên là đồ thị của ba hàm số $y = {a^x}$, $y = {b^x}$, $y = {c^x}$. Khẳng định nào sau đây là đúng?
Trả lời bởi giáo viên
Đáp án đúng: c
Ta thấy hàm $y = {c^x}$ có đồ thị từ trái sang phải theo hướng đi lên nên là hàm đồng biến \( \Rightarrow c > 1.\) Còn hàm số $y = {a^x}$ và $y = {b^x}$ là những hàm nghịch biến \( \Rightarrow a,{\rm{ }}b < 1.\) Từ đó loại được các đáp án A, D.
Từ đồ thị hàm số ta thấy tại cùng một giá trị ${x_0} < 0$ thì đồ thị hàm số $y = {b^x}$ nằm trên đồ thị hàm số $y = {a^x}$ hay \(\left\{ \begin{array}{l}x < 0\\{b^x} > {a^x}\end{array} \right. \Rightarrow b < a\).
Ví dụ \(\left\{ \begin{array}{l}x = - 1\\{b^{ - 1}} > {a^{ - 1}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\\dfrac{1}{b} > \dfrac{1}{a}\end{array} \right. \to b < a.\)
Vậy $c > a > b.$
Hướng dẫn giải:
- Bước 1: Quan sát các đồ thị, nhận xét về tính đơn điệu để nhận xét các cơ số.
+ Hàm số đồng biến thì cơ số lớn hơn \(1\).
+ Hàm số nghịch biến thì cơ số lớn hơn \(0\) và nhỏ hơn \(1\).
- Bước 2: So sánh các cơ số dựa vào phần đồ thị của hàm số.
- Bước 3: Kết hợp các điều kiện ở trên ta được mối quan hệ cần tìm.
