Hàm số mũ

Hàm số xác định và liên tục trên \(\mathbb{R}.\)

Ta có $y' = {e^x} + x{e^x} = {e^x}\left( {1 + x} \right)$$ \Rightarrow y' = 0 \Leftrightarrow 1 + x = 0 \Leftrightarrow x =  - 1$

Bảng biến thiên

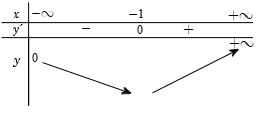
Từ bảng biến thiên, suy ra hàm số có giá trị cực tiểu \({y_{{\rm{CT}}}} = y\left( { - 1} \right) =  - \dfrac{1}{e}\).

Ta có

$ \bullet {\rm{  }}{f^2}\left( x \right) - {g^2}\left( x \right) = {\left( {\dfrac{{{a^x} + {a^{ - x}}}}{2}} \right)^2} - {\left( {\dfrac{{{a^x} - {a^{ - x}}}}{2}} \right)^2} = 1$ hay khẳng đinh 1 đúng.

\( \bullet {\rm{  }}g\left( {2x} \right) = \dfrac{{{a^{2x}} - {a^{ - 2x}}}}{2} = \dfrac{{\left( {{a^x} - {a^{ - x}}} \right)\left( {{a^x} + {a^{ - x}}} \right)}}{2}\)\( = 2.\dfrac{{{a^x} - {a^{ - x}}}}{2}.\dfrac{{{a^x} + {a^{ - x}}}}{2} = 2g\left( x \right).f\left( x \right)\)  hay khẳng đinh 2 đúng.

\( \bullet {\rm{  }}\left\{ \begin{array}{l}f\left( {g\left( 0 \right)} \right) = f\left( 0 \right) = 1.\\g\left( {f\left( 0 \right)} \right) = g\left( 1 \right) = \dfrac{{a - \dfrac{1}{a}}}{2} = \dfrac{{{a^2} - 1}}{{2a}}\end{array} \right.\) \( \Rightarrow f\left( {g\left( 0 \right)} \right) \ne g\left( {f\left( 0 \right)} \right)\) hay khẳng định 3 sai.

\( \bullet {\rm{  }}\)Do \(g\left( {2x} \right) = 2g\left( x \right)f\left( x \right)\), lấy đạo hàm hai vế (để ý là \(\left[ {g\left( u \right)} \right]' = u'g'\left( u \right)\)), ta có:

\(\left[ {g\left( {2x} \right)} \right]' = 2\left[ {g'\left( x \right)f\left( x \right) + g\left( x \right)f'\left( x \right)} \right]\)\( \Leftrightarrow 2g'\left( {2x} \right) = 2\left[ {g'\left( x \right)f\left( x \right) + g\left( x \right)f'\left( x \right)} \right]\)

\( \Leftrightarrow g'\left( {2x} \right) = g'\left( x \right)f\left( x \right) + g\left( x \right)f'\left( x \right)\) hay khẳng định 4 sai.

Vậy có 2 khẳng định đúng.

Hàm số xác định $ \Leftrightarrow {e^x} - 1 \ne 0 \Leftrightarrow {e^x} \ne 1 \Leftrightarrow x \ne 0$.

Ta có: \(y = {\left( {\dfrac{1}{2}} \right)^{ - x}} = \dfrac{1}{{{{\left( {\dfrac{1}{2}} \right)}^x}}} = \dfrac{1}{{\dfrac{1}{{{2^x}}}}} = {2^x}\) nên hai hàm số \(y = {2^x}\) và \(y = {\left( {\dfrac{1}{2}} \right)^{ - x}}\) là một. Do đó chúng có chung đồ thị.

Vì \({\left( {\dfrac{1}{3}} \right)^x}\) và \( - {\left( {\dfrac{1}{3}} \right)^x}\) đối nhau nên đồ thị hai hàm số đó đối xứng nhau qua \(Ox\).

Dáng đồ thị là của hàm số \(y = {a^x}\) với \(a > 1\) nên loại A và C.

Đồ thị hàm số đi qua điểm \(\left( {1;3} \right)\) nên chỉ có D thỏa mãn.

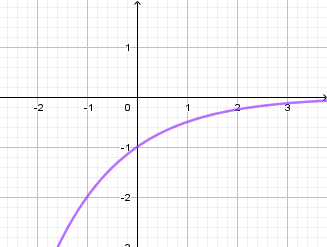
Quan sát đồ thị ta thấy nó nằm hoàn toàn phía dưới trục hoành nên loại A và B.

Lại có, đồ thị hàm số đi qua điểm \(\left( { - 1; - 2} \right)\) nên thay tọa độ điểm này vào các hàm số C và D ta được đáp án C.

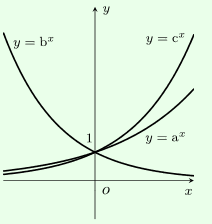
Ta thấy:

- Hàm số \(y = {b^x}\) nghịch biến nên \(0 < b < 1\).

- Hàm số \(y = {a^x},y = {c^x}\) đồng biến nên \(a,c > 1 > b\), loại B và D.

- Xét phần đồ thị hai hàm số \(y = {a^x},y = {c^x}\) ta thấy phần đồ thị hàm số \(y = {c^x}\) nằm trên đồ thị hàm số \(y = {a^x}\) nên \({c^x} > {a^x},\forall x > 0 \Leftrightarrow c > a\).

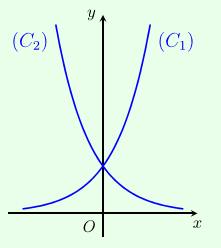
Ta thấy: Đồ thị hàm số \(y = {b^x}\) đi xuống nên hàm số \(y = {b^x}\) nghịch biến nên \(0 < b < 1\).

Đồ thị hàm số \(y = {a^x}\) đi lên nên hàm số \(y = {a^x}\) đồng biến nên \(a > 1\).

Vậy \(0 < b < 1 < a\).

Hàm số xác định $ \Leftrightarrow 1 - {3^{{x^2} - 5x + 6}} \ge 0 \Leftrightarrow {3^{{x^2} - 5x + 6}} \le 1$

$ \Leftrightarrow {x^2} - 5x + 6 \le 0 \Leftrightarrow 2 \le x \le 3$.

Vậy tập xác định của hàm số là $D=[2;3]$.

Đạo hàm $f'\left( x \right) = \left( {{x^\pi }} \right)'.{\pi ^x} + {x^\pi }.\left( {{\pi ^x}} \right)' = \pi .{x^{\pi  - 1}}.{\pi ^x} + {x^\pi }.{\pi ^x}.\ln \pi $

Suy ra \(f'\left( 1 \right) = {\pi ^2} + \pi \ln \pi \).

Tập xác định của hàm số \(y = {2^x}\) là \(\mathbb{R}.\)

Có $y = {2^{\ln x + {x^2}}} \Rightarrow y' = \left( {\dfrac{1}{x} + 2x} \right){2^{\ln x + {x^2}}}.\ln 2$

Ta có: \(y = {3^x} + \ln 3 \Rightarrow y' = {3^x}\ln 3\)

Lại có: \(y = {3^x} + \ln 3 \Rightarrow {3^x} = y - \ln 3 \Rightarrow y' = \left( {y - \ln 3} \right)\ln 3 = y\ln 3 - {\ln ^2}3\) 

Ta có: \(I = \mathop {\lim }\limits_{x \to 0} \dfrac{{{e^{3x}} - {e^{2x}}}}{x} = \mathop {\lim }\limits_{x \to 0} \dfrac{{\left( {{e^{3x}} - 1} \right) - \left( {{e^{2x}} - 1} \right)}}{x} \)

$= \mathop {\lim }\limits_{x \to 0} \left[ {3.\dfrac{{{e^{3x}} - 1}}{{3x}} - 2.\dfrac{{{e^{2x}} - 1}}{{2x}}} \right] = 3.1 - 2.1 = 1$

Do đó, thay \(I = 1\) vào các đáp án ta được đáp án B.

Vậy khi \(a \ne 1\) thì $\left( {a - 1} \right)\left( {{x_1} - {x_2}} \right) < 0$

$\begin{array}{l}f\left( x \right) < 1 \Leftrightarrow {2^x}{.7^{{x^2}}} < 1 \Leftrightarrow {7^{{x^2}}} < {2^{ - x}} \Leftrightarrow {x^2}.\ln 7 <  - x.\ln 2 \Leftrightarrow x\ln 2 + {x^2}\ln 7 < 0\\ \Leftrightarrow x + {x^2}{\log _2}7 < 0\\ \Leftrightarrow x{\log _7}2 + {x^2} < 0\end{array}$

Đối chiếu các đáp án thấy câu D sai.

Ta có: \(C\left( {0;2} \right)\)

\(\begin{array}{l}{a^x} = 2 \Rightarrow x = {\log _a}2 \Rightarrow A({\log _a}2;2)\\{b^x} = 2 \Leftrightarrow x = {\log _b}2 \Rightarrow B({\log _b}2;2)\end{array}\)

Vì C nằm giữa A và B và

\(\begin{array}{l}AC = 2BC \Leftrightarrow \overrightarrow {AC}  =  - 2\overrightarrow {BC}  \Leftrightarrow \left\{ \begin{array}{l} - {\log _a}2 = 2.{\log _b}2\\0 = 0\end{array} \right. \Leftrightarrow  - \dfrac{1}{{{{\log }_2}a}} = 2.\dfrac{1}{{{{\log }_2}b}}\\ \Leftrightarrow {\log _2}b =  - 2{\log _2}a \Leftrightarrow {\log _2}b = {\log _2}{a^{ - 2}} \Leftrightarrow b = {a^{ - 2}}\end{array}\)

Ta có:

\(f'\left( x \right) = \left( {3{x^2} - 3} \right){e^{{x^3} - 3x + 3}} = 0 \Leftrightarrow 3{x^2} - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 \in \left[ {0;2} \right]\\x =  - 1 \notin \left[ {0;2} \right]\end{array} \right.\)

\(f\left( 0 \right) = {e^3};f\left( 1 \right) = e;f\left( 2 \right) = {e^5}\) nên \(\mathop {\min }\limits_{\left[ {0;2} \right]} f\left( x \right) = f\left( 1 \right) = e\) và \(\mathop {\max }\limits_{\left[ {0;2} \right]} f\left( x \right) = f\left( 2 \right) = {e^5}\).

Vậy \(m = {e^5}\).

Ta có: \(f'\left( x \right) =  - 3{e^{2 - 3x}} < 0,\forall x \in R\).

Do đó hàm số \(f\left( x \right)\) lên tục và nghịch biến trên \(\left[ {0;2} \right]\).

Do đó \(m = \mathop {\min }\limits_{\left[ {0;2} \right]} f\left( x \right) = f\left( 2 \right) = \dfrac{1}{{{e^4}}};M = \mathop {\max }\limits_{\left[ {0;2} \right]} f\left( x \right) = f\left( 0 \right) = {e^2} \Rightarrow M.m = \dfrac{1}{{{e^2}}}\)