Trả lời bởi giáo viên
Đáp án đúng: c
Hàm số xác định và liên tục trên \(\mathbb{R}.\)
Ta có $y' = {e^x} + x{e^x} = {e^x}\left( {1 + x} \right)$$ \Rightarrow y' = 0 \Leftrightarrow 1 + x = 0 \Leftrightarrow x = - 1$
Bảng biến thiên
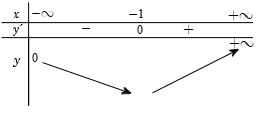
Từ bảng biến thiên, suy ra hàm số có giá trị cực tiểu \({y_{{\rm{CT}}}} = y\left( { - 1} \right) = - \dfrac{1}{e}\).
Hướng dẫn giải:
- Tính \(y'\) và giải phương trình \(y' = 0\)
- Lập bảng biến thiên từ đó suy ra giá trị cực tiểu của hàm số.

