Đồ thị tọa độ - thời gian của chất điểm chuyển động thẳng đều:
\(x = {x_0} + vt\) dạng đồ thị giống đồ thị của hàm số \(y = ax + b\)
đồ thị là đường thẳng có thể không đi qua gốc tọa độ
Đồ thị tọa độ - thời gian trong chuyển động thẳng của chất điểm có dạng như hình vẽ. Trong khoảng thời gian nào chất điểm chuyển động thẳng đều?
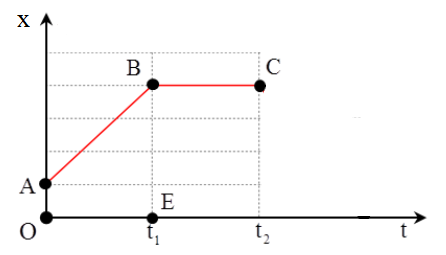
Từ đồ thị ta có:
+ Từ 0 đến t1: vật chuyển động thẳng đều
+ Từ t1 đến t2: vật đứng yên
Một vật chuyển động thẳng đều với phương trình \(x = {x_0} + v(t - {t_0})\). Kết luận nào dưới dây là sai?
A, C, D - đúng
B- sai vì:
+ Tại thời điểm \(t_0\) vật có tọa độ \(x_1=x_0\)
+ Tại thời điểm \(t\) vật có tọa độ \(x_2=x_0+v(t-t_0)\)
=> Độ dời từ thời điểm t0 tới thời điểm t là \(\Delta x = x_2 -x_1 =v(t - {t_0})\)
Hình sau cho biết đồ thị tọa độ của một chiếc xe chuyền động trên đường thẳng. Vận tốc của xe là:
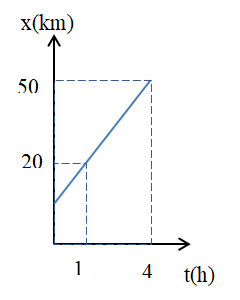
Theo đồ thị: lúc t1 = 1 h, x1 = 20 km; lúc t2 = 4 h, x2 = 50 km
\( \to v = \frac{{{x_2} - {x_1}}}{{{t_2} - {t_1}}} = \frac{{50 - 20}}{{4 - 1}} = 10(km/h)\)
Hình sau cho biết đồ thị tọa độ của một xe chuyển động thẳng. Vận tốc của nó là 5 m/s. x0 = ?
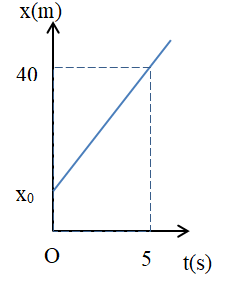
Ta có:
+ Phương trình chuyển động: \(x = {x_o} + 5t{\rm{ }}\)
+ Tại thời điểm t = 5s, x = 40 m \( \to 40 = {x_0} + 5.5 \to {x_0} = 15m\)
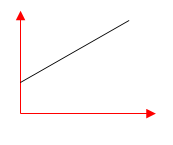
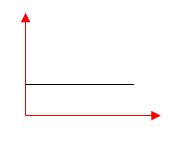
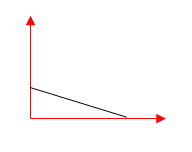
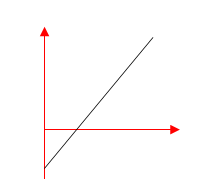
Trong các đồ thị $x – t$ dưới đây, đồ thị nào không biểu diễn chuyển động thẳng đều.
Đồ thị không biểu diễn chuyển động thẳng đều là B
Chất điểm chuyển động trên đường thẳng, vật xuất phát từ gốc tọa độ chuyển động theo chiều dương, tại các thời điểm khác nhau vật có vị trí tọa độ như bảng dưới:

Phương trình chuyển động của vật là:
Ta có:
+ Chất điểm chuyển động trên đường thẳng, vật xuất phát từ gốc tọa độ chuyển động theo chiều dương
+ Vận tốc: \(v = \frac{{\Delta {x_1}}}{{\Delta {t_1}}} = \frac{{2,5 - 0}}{{1 - 0}} = 2,5(m/s)\)
+ Tại thời điểm ban đầu: \({t_0} = 0;{x_0} = 0\)
=> Phương trình chuyển động của vật: \(x = {x_0} + vt = 2,5t\)
Một chất điểm chuyển động thẳng đều có đồ thị tọa độ thời gian như hình vẽ. Phương trình chuyển động của vật là:
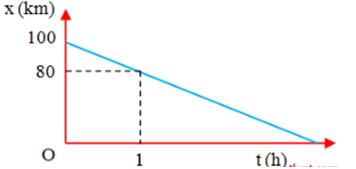
Phương trình chuyển động: \(x = {x_0} + vt\)
Từ đồ thị x-t, ta có:
+ Tại thời điểm \({t_0} = 0\) : \({x_0} = 100km\)
+ Tại \(t = 1h\): \(x = 80km = {x_0} + v.1 \to v = \frac{{80 - 100}}{1} = - 20(km/h)\)
=> phương trình chuyển động của vật: \(x = 100 - 20t{\rm{ }}(km)\)
Lúc 7h một oto chuyển động từ A đến B với vận tốc 80km/h. Cùng lúc một oto chuyển động từ B về A với vận tốc 80km/h. Biết khoảng cách từ A đến B là 200km, coi chuyển động của hai oto là chuyển động thẳng đều . Hai xe gặp nhau tại vị trí cách A là bao nhiêu? Khi đó đồng hồ chỉ mấy h?
Chọn chiều (+) là chiều từ A đến B, gốc thời gian là lúc 7h, gốc tọa độ tại điểm A
Phương trình chuyển động của 2 oto là:
\(\begin{array}{l}{x_1} = {x_{01}} + 80t\\{x_2} = {x_{02}} - 80t\end{array}\)
Tại thời điểm ban đầu: \({t_0} = 0\) (lúc đồng hồ chỉ 7h)
+ oto 1 đang ở A \( \to {x_{01}} = 0 \to {x_1} = 80t{\rm{ }}(km)\)
+ oto 2 đang ở B cách A 200km \( \to {x_{02}} = 200 \to {x_2} = 200 - 80t{\rm{ }}(km)\)
Hai xe gặp nhau khi: \({x_1} = {x_2} \leftrightarrow 80t = 200 - 80t \to t = 1,25h\)
Thay vào phương trình của xe 1, ta được vị trí gặp nhau: \(x = {x_1}(t = 1,25h) = 80.1,25 = 100(km)\)
=> Hai xe gặp nhau sau 1,25h (lúc 8,25h hay 8h15’) chuyển động và tại vị trí cách điểm A 100km, cách B 100km
Một oto chuyển động thẳng đều từ A đến B với vận tốc 90km/h. Sau 15phút từ B một xe máy chuyển động về A với vận tốc 40km/h. Sau khi đến B oto dừng lại nghỉ 30 phút rồi chuyển động thẳng đều quay trở lại A và gặp xe máy lần 2 ở điểm cách A là 25km (chưa đến A) . Độ dài quãng đường AB là:
Ta có:
+ 15phút = 0,25h, 30 phút = 0,5h
Chọn gốc thời gian là lúc xe máy bắt đầu đi, chiều dương từ A đến B, gốc tại A
Tọa độ gặp nhau lần thứ 2 của xe máy: \({x_2} = AB - 40t = 25 \to t = \frac{{AB - 25}}{{40}}{\rm{ (1)}}\)
Xe máy xuất phát sau oto 15phút, oto nghỉ 30 phút => trong quãng thời gian chuyển động của xe máy oto xuất phát chậm hơn 15phút = 0,25h
Tọa độ gặp nhau lần thứ 2 của oto:
\({x_1} = 2{\rm{A}}B - 90(t - 0,25) = 25{\rm{ (2)}}\)
Từ (1) và (2), ta có:
\(2AB - 90(\frac{{AB - 25}}{{40}} - 0,25) = 25 \to AB = 215(km)\)
Xe bus chuyển động thẳng đều trên đường với \({v_1} = 16m/s\). Một hành khách đứng cách đường một đoạn \(a = 60m\), người này nhìn thấy xe bus vào thời điểm xe cách người một khoảng \(b = 400m\). Nếu muốn gặp xe với vận tốc nhỏ nhất thì người này phải chạy với vận tốc là bao nhiêu?
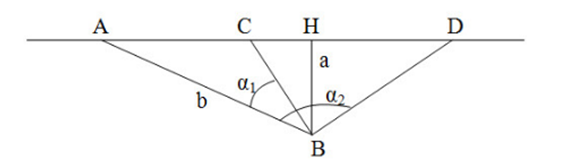
Nếu muốn vận tốc là nhỏ nhất => quãng đường đi là nhỏ nhất => người đó đi theo hướng BH
Từ hình ta có: \(AH = \sqrt {{b^2} - {a^2}} = \sqrt {{{400}^2} - {{60}^2}} \approx 395.5(m)\)
Ta có: \(\frac{{BH}}{{{v_{\min }}}} = \frac{{AH}}{{{v_1}}} \to {v_{\min }} = \frac{{BH}}{{AH}}.{v_1} = \frac{{60}}{{395,5}}.16 = 2,4(m/s)\)
Một ôtô chuyển động trên một quãng đường từ $A$ đến $B$ mất một khoảng thời gian $t$, vận tốc xe đi trong một nửa thời gian đầu là $42km/h$, vận tốc xe đi trong nửa khoảng thời gian cuối là $60km/h$. Tốc độ trung bình của ôtô trên cả quãng đường là:
Ta có:
+ Nửa thời gian đầu: \(\dfrac{t}{2} = \dfrac{{{s_1}}}{{{v_1}}} \to {s_1} = {v_1}\dfrac{t}{2}\)
+ Nửa thời gian sau: \(\dfrac{t}{2} = \dfrac{{{s_2}}}{{{v_2}}} \to {s_2} = {v_2}\dfrac{t}{2}\)
Vận tốc của ôtô trên cả quãng đường: \({v_{tb}} = \dfrac{{{s_1} + {s_2}}}{t} = \dfrac{{{v_1} + {v_2}}}{2} = \dfrac{{42 + 60}}{2} = 51km/h\)
Một ôtô chuyển động trên đoạn đường thẳng. Trong $1/2$ quãng đường đầu đi với vận tốc $40km/h$ , trong $1/2$ quãng đường còn lại ôtô đi với vận tốc như sau: trong $1/2$ thời gian đầu với vận tốc $75km/h$ và trong $1/2$ thời gian cuối với vận tốc $45km/h$. Tốc độ trung bình trên đoạn đường là:
Ta có:
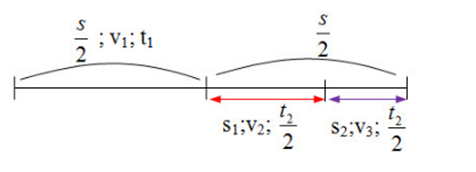
\(\begin{array}{l}{t_1} = \dfrac{{\dfrac{s}{2}}}{{{v_1}}} = \dfrac{s}{{80}}\\\dfrac{{{t_2}}}{2} = \dfrac{s_1}{{v{}_2}} = \dfrac{s_2}{v_3} \to 3{{\rm{s}}_1} = 5{{\rm{s}}_2}\end{array}\)
Mặt khác, ta có:
\(\begin{array}{l}{s_1} + {s_2} = \dfrac{s}{2}\\ \to {s_1} = \dfrac{{5{\rm{s}}}}{{16}};{s_2} = \dfrac{{3{\rm{s}}}}{{16}}\\ \to {t_2} = \dfrac{{2{{\rm{s}}_1}}}{{{v_2}}} = \dfrac{{5{\rm{s}}}}{{8{v_2}}} = \dfrac{s}{{120}}\\{v_{tb}} = \dfrac{s}{{{t_1} + {t_2}}} = \dfrac{s}{{\dfrac{s}{{80}} + \dfrac{s}{{120}}}} = 48km/h\end{array}\)
Một ca-nô rời bến chuyển động thẳng đều. Đầu tiên, ca-nô chạy theo hướng nam bắc trong thời gian $2$ phút $40$ giây rồi tức thì rẽ sang hướng đông tây và chạy thêm $2$ phút với vận tốc như trước và dừng lại. Khoảng cách từ nơi xuất phát tới nơi dừng lại là $1km$. Vận tốc của ca-nô là:
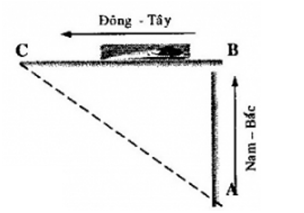
Đổi đơn vị, ta có: $2$ phút $40$ giây = $160s$; $2$ phút = $120s$
$1km = 1000m$
Gọi A - điểm xuất phát; B- điểm bắt đầu rẽ, C- điểm dừng lại của ca-nô
Ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} = {\left( {v{t_1}} \right)^2} + {\left( {v{t_2}} \right)^2}\\ \to v = \dfrac{{AC}}{{\sqrt {t_1^2 + t_2^2} }} = \dfrac{{1000}}{{\sqrt {{{160}^2} + {{120}^2}} }} = 5m/s = 18km/h\end{array}\)
Một thanh cứng, mảnh $AB$ có chiều dài \(l = 2m\) dựng đứng sát bức tường thẳng đứng như hình. Ở đầu $A$ của thanh có một con kiến. Khi đầu $A$ của thanh bắt đầu chuyển động trên sàn ngang về bên phải theo phương vuông góc với bức tường thì con kiến cũng bắt đầu bò dọc theo thanh. Đầu $A$ chuyển động thẳng đều với vận tốc \({v_1} = 0,5cm/s\) so với sàn kể từ vị trí tiếp xúc với bức tường. Con kiến bò thẳng đều với vận tốc \({v_2} = 0,2cm/s\) so với thanh kể từ đầu $A$. Độ cao cực đại của con kiến đối với sàn ngang là bao nhiêu? Biết rằng đầu B của thanh luôn tiếp xúc với tường.
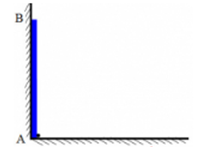
Ta có:
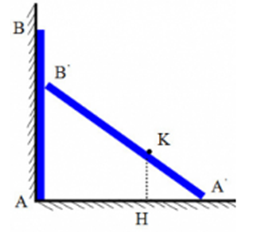
+ Khi đầu $A$ của thanh di chuyển từ $A$ đến $A’$ thì con kiến di chuyển từ $A’$ đến $K$ trong cùng một khoảng thời gian.
+ Khi đó: \(\dfrac{{{s_{{\rm{AA'}}}}}}{{{v_1}}} = \dfrac{{{s_{A'K}}}}{{{v_2}}} \to \dfrac{{{s_{{\rm{AA'}}}}}}{{{s_{A'K}}}} = \dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{0,5}}{{0,2}} = 2,5\)
=> Nếu quãng đường con kiến di chuyển là \({s_{A'K}} = x \to {s_{AA'}} = 2,5x\)
Từ hình, ta có:
\({\left( {AB'} \right)^2} = {2^2} - {\left( {2,5{\rm{x}}} \right)^2} = 4 - 6,25{{\rm{x}}^2}\)
Mặt khác, ta có:
\(\begin{array}{l}\Delta A'KH \sim \Delta A'B'A\\ \to \dfrac{{HK}}{{AB'}} = \dfrac{{A'K}}{{A'B'}}\\ \to H{K^2} = {\left( {AB'} \right)^2}{\left( {\dfrac{{A'K}}{{A'B'}}} \right)^2} = (4 - 6,25{{\rm{x}}^2})\dfrac{{x{}^2}}{4} = - 1,5625{{\rm{x}}^4} + {x^2}\end{array}\)
Để HK có giá trị cực đại thì: \({x^2} = - \dfrac{b}{{2{\rm{a}}}} = \dfrac{1}{{2.1,5625}} = 0,32\)
Khi đó: \(H{K_{{\rm{max}}}} = \sqrt { - 1,5625.0,{{32}^2} + 0,32} = 0,4(m)\)
Ba xe chuyển động trên cùng một đường thẳng. Đường biểu diễn tọa độ theo thời gian của ba xe I, II, III dưới hình sau:
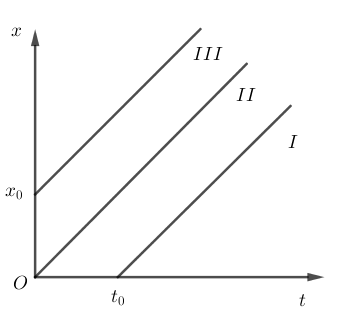
Tìm câu sai.
A, C, D – đúng
B – sai vì: Các đồ thị I, II, III biểu diễn tọa độ theo thời gian là những đường thẳng xiên góc, song song với nhau => Chuyển động của ba xe là thẳng đều với cùng tốc độ.
Ba xe chuyển động trên cùng một đường thẳng. Đường biểu diễn tọa độ theo thời gian của ba xe I, II, III dưới hình sau:

Phương trình chuyển động của các xe là:
Các đồ thị I, II, III biểu diễn tọa độ theo thời gian là những đường thẳng xiên góc, song song với nhau => Chuyển động của ba xe là thẳng đều với cùng tốc độ \(v\)
+ Xe I: xuất phát lúc \({t_0}\) tại gốc tọa độ
\( \Rightarrow \) Phương trình chuyển động của xe I: \({x_1} = v\left( {t - {t_0}} \right)\)
+ Xe II: xuất phát tại gốc tọa độ
\( \Rightarrow \) Phương trình chuyển động của xe II: \({x_2} = vt\)
+ Xe III: xuất phát tại vị trí cách gốc tọa độ một đoạn \({x_0}\)
\( \Rightarrow \) Phương trình chuyển động của xe III: \({x_3} = {x_0} + vt\)
Lúc \(8\) giờ \(30\) phút, một xe ô-tô chuyển động từ A đến B cách nhau \(150km\) với vận tốc \(80km/h\). Cùng lúc đó, một ô-tô chuyển động từ B đến A với vận tốc \(40km/h\). Chọn gốc tọa độ là B, chiều dương từ B đến A, gốc thời gian lúc hai xe bắt đầu chuyển động. Coi đoạn đường AB là thẳng.
Phương trình chuyển động của hai xe có dạng:
Ta có:
+ Chọn gốc tọa độ là B, chiều dương từ B đến A, gốc thời gian lúc hai xe bắt đầu chuyển động

+ Phương trình chuyển động của mỗi xe:
- Xe tại B: \({x_B} = {x_{0B}} + {v_B}t = 0 + 40t = 40t\)
- Xe tại A: \({x_A} = {x_{0A}} + {v_A}t = AB - 80t = 150 - 80t\)
Lúc \(8\) giờ \(30\) phút, một xe ô-tô chuyển động từ A đến B cách nhau \(150km\) với vận tốc \(80km/h\). Cùng lúc đó, một ô-tô chuyển động từ B đến A với vận tốc \(40km/h\). Chọn gốc tọa độ là B, chiều dương từ B đến A, gốc thời gian lúc hai xe bắt đầu chuyển động. Coi đoạn đường AB là thẳng.
Hai xe gặp nhau lúc mấy giờ? Nơi gặp nhau cách A bao nhiêu km?
Ta có:
+ Chọn gốc tọa độ là B, chiều dương từ B đến A, gốc thời gian lúc hai xe bắt đầu chuyển động

+ Phương trình chuyển động của mỗi xe:
- Xe tại B: \({x_B} = {x_{0B}} + {v_B}t = 0 + 40t = 40t\)
- Xe tại A: \({x_A} = {x_{0A}} + {v_A}t = AB - 80t = 150 - 80t\)
+ Hai xe gặp nhau khi \({x_A} = {x_B}\)
\(\begin{array}{l} \Leftrightarrow 150 - 80t = 40t\\ \Leftrightarrow 150 = 120t\\ \Rightarrow t = 1,25h\end{array}\)
Thay vào \({x_B}\) ta được: \({x_B} = 40.1,25 = 50km\)
Vậy 2 xe gặp nhau vào thời điểm \(\left( {8h30 + 1,25h = 9h45} \right)\) tại vị trí cách A \(\left( {AB - {x_B} = 150 - 50 = 100km} \right)\)
Lúc 7 giờ, một người ở A chuyển động thẳng đều với v = 36 km/h đuổi theo người ở B đang chuyển động với v = 5 m/s. Biết AB = 18 km. Hai người gặp nhau lúc mấy giờ và cách A bao nhiêu kilomet?
Đổi: \(v = 5m/s = 18km/h\)
Chọn gốc toạ độ tại A, chiều dương là chiều chuyển động, gốc thời gian lúc 7 giờ.
Phương trình chuyển động của hai người là:
\(\left\{ \begin{array}{l}{x_A} = 36t\,\,\left( {km} \right){\rm{ }}\\{x_B} = {x_0} + {v_B}.t = 18 + 18t\,\,\left( {km} \right)\end{array} \right.\)
Hai người gặp nhau khi: \({x_A} = {x_B} \Leftrightarrow 36t = 18 + 18t \Rightarrow t = 1h\)
Vậy hai người gặp nhau lúc \(8h.\)
Vị trí hai người gặp nhau cách A: \({x_A} = 36.1 = 36km\)