Cùng một lúc tại hai điểm A và B cách nhau 45km có hai ô tô xuất phát, chạy cùng chiều nhau trên đường thẳng AB, theo chiều từ A đến B. Vận tốc của ô tô chạy từ A là 54km/h và của ô tô chạy từ B là 45km/h. Chọn A làm mốc, chọn thời điểm xuất phát của hai xe ô tô làm mốc thời gian và chọn chiều chuyển động của hai ô tô làm chiều dương. Khoảng cách từ A đến địa điểm hai xe gặp nhau là?
Chọn A làm mốc, chọn thời điểm xuất phát của hai xe ô tô làm mốc thời gian và chọn chiều chuyển động của hai ô tô làm chiều dương.
Theo dữ kiện của đề bài thì :
+ Tọa độ ban đầu của xe A: \({x_{0A}} = 0km\)
+ Vận tốc của xe A: \({v_A} = 54km/h\)
→ PT chuyển động của ô tô chạy từ A là: \({x_A} = 54t\,\,\left( {km} \right)\)
+ Tọa độ ban đầu của xe B: \({x_{0B}} = 45km\)
+ Vận tốc của xe B: \({v_B} = 45km/h\)
→ PT chuyển động của ô tô chạy từ A là: \({x_B} = 45t + 45\,\,\left( {km} \right)\)
Ô tô A đuổi kịp ô tô B thì:
\({x_A} = {x_B}\)\( \Leftrightarrow 54t = 45t + 45 \Rightarrow t = 5h\)
Khi đó vị trí gặp nhau cách A khoảng: \(d = 54.5 = 270km\)
Hình vẽ là đồ thị toạ độ - thời gian của một chiếc ô tô chạy từ A đến B trên một đường thẳng. Điểm A cách gốc tọa độ bao nhiêu kilômét ? Thời điểm xuất phát cách mốc thời gian mấy giờ ?
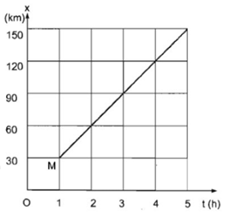
Vật xuất phát tại A trùng với điểm M (30;1) trên đồ thị (x;t) nên A cách O 30 km và xe xuất phát lúc 1h.
Một ôtô chuyển động thẳng đều có phương trình chuyển động \(x = 5 + 40.t\), \(x\) tính bằng \(km\) và \(t\) tính bằng giờ. Biết ôtô chuyển động không đổi chiều. Tính quãng đường ôtô đi được sau \(2h.\)
Phương trình chuyển động của ô tô: \(x = 5 + 40.t \Rightarrow v = 40km/h\)
Quãng đường ô tô đi được sau 2h là: \(S = vt = 40.2 = 80km\)
Vào lúc 14h, hai oto chuyển động thẳng đều cùng chiều đi qua các thành phố A và B cách nhau 150km. Chiều chuyển động của các xe từ A đến B. Ôtô qua thành phố A có vận tốc 75km/h. Ôtô qua thành phố B có vận tốc 50 km/h. Hai xe gặp nhau tại vị trí cách B bao nhiêu km?
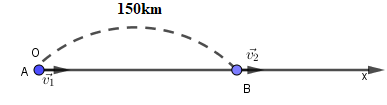
Chọn gốc tọa độ tại A, chiều dương chọn là chiều từ A hướng B. Chọn gốc thời gian là lúc 14h
Giả sử phương trình chuyển động của ô tô qua A có dạng:
\({x_A} = {x_{0A}} + {v_A}\left( {t - {t_{0A}}} \right)\)
Với: \(\left\{ \begin{array}{l}{x_{0A}} = 0\\{t_{0A}} = 0\\{v_A} = 75km/h\end{array} \right. \Rightarrow {x_A} = 0 + 75\left( {t - 0} \right) = 75t\,\,\left( {km} \right)\)
Giả sử phương trình chuyển động của ô tô qua B có dạng:
\({x_B} = {x_{0B}} + {v_B}\left( {t - {t_{0B}}} \right)\)
Với: \(\left\{ \begin{array}{l}{x_{0B}} = 150km\\{t_{0B}} = 0\\{v_B} = 50km/h\end{array} \right. \Rightarrow {x_B} = 150 + 50t\,\,\left( {km} \right)\)
Hai xe gặp nhau khi: \({x_A} = {x_B} \Rightarrow 75t = 150 + 50t \Rightarrow t = 6h\)
Thay t = 6h vào phương trình ta có: \({x_A} = 75.6 = 450\left( {km} \right)\)
Vị trí hai xe gặp nhau cách B: \(d = 450 - 150 = 300\left( {km} \right)\)