Cho đồ thị tọa độ - thời gian của một ô-tô chạy từ A đến B trên một đường thẳng như hình vẽ.
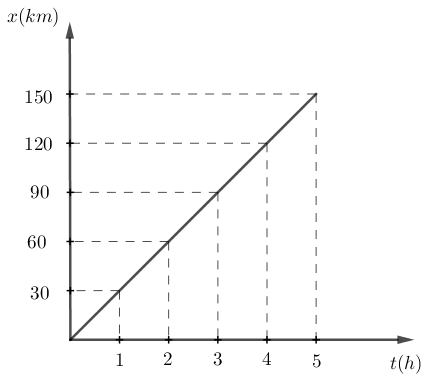
Dựa vào đồ thị, viết phương trình chuyển động của ô-tô là:
Từ đồ thị ta có:
+ Tại thời điểm ban đầu \({t_0} = 0\): \({x_0} = 0\)
+ Tại thời điểm \({t_1} = 1h\): \({x_1} = 30km\)
\( \Rightarrow v = \dfrac{{{x_1} - {x_0}}}{{{t_1} - {t_0}}} = \dfrac{{30 - 0}}{{1 - 0}} = 30km/h\)
\( \Rightarrow \) Phương trình chuyển động của vật: \(x = {x_0} + vt = 0 + 30t = 30t\) \(\left( {km;h} \right)\)
Trên trục \(x'Ox\) có hai ô-tô chuyển động với phương trình tọa độ lần lượt là \({x_1}\left( t \right) = - 20t + 100\) và \({x_2}\left( t \right) = 10t - 50\) (t tính bằng đơn vị giây \(\left( {t > 0} \right)\), còn x tính bằng đơn vị mét). Khoảng cách giữa hai ô-tô lúc \(t = 2s\) là
Ta có, khoảng cách giữa hai xe: \(\Delta x = \left| {{x_1}\left( t \right) - {x_2}\left( t \right)} \right|\)
Tại thời điểm \(t = 2s\) ta có: \(\left\{ \begin{array}{l}{x_1} = - 20.2 + 100 = 60m\\{x_2} = 10.2 - 50 = - 30m\end{array} \right.\)
\( \Rightarrow \) Khoảng cách giữa hai ô-tô lúc \(t = 2s\) là: \(\Delta x = \left| {{x_1} - {x_2}} \right| = \left| {60 - \left( { - 30} \right)} \right| = 90m\)
Từ hai địa điểm A và B cách nhau \(180km\) có hai xe khởi hành cùng một lúc, chạy ngược chiều nhau. Xe từ A có vận tốc \({v_1} = 36km/h\), xe từ B có vận tốc \({v_2} = 54km/h\). Chọn địa điểm A làm gốc tọa độ, gốc thời gian là lúc hai xe khởi hành, chiều từ A đến B là chiều dương. Thời điểm hai xe tới gặp nhau và tọa độ của địa điểm hai xe gặp nhau là:

Ta có:
+ Chọn địa điểm A làm gốc tọa độ, gốc thời gian là lúc hai xe khởi hành, chiều dương từ A đến B
+ Phương trình chuyển động của mỗi xe:
- Xe tại A: \({x_A} = {x_{0A}} + {v_A}t = 0 + 36t\)
- Xe tại B: \({x_B} = {x_{0B}} + {v_B}t = 180 - 54t\)
+ Hai xe gặp nhau khi \({x_A} = {x_B}\)
\(\begin{array}{l} \Leftrightarrow 36t = 180 - 54t\\ \Leftrightarrow 90t = 180\\ \Rightarrow t = 2h\end{array}\)
Thay \(t = 2h\) vào phương trình xe A, ta được vị trí hai xe gặp nhau\(x = {x_A} = 36.2 = 72km\)
Vậy hai xe gặp nhau sau \(t = 2h\) kể từ lúc xuất phát tại vị trí \(x = 72km\)
Xe bus chuyển động thẳng đều trên đường với \({v_1} = 54km/h\). Một hành khách đứng cách đường một đoạn \(a = 40m\), người này nhìn thấy xe bus vào thời điểm xe cách người một khoảng \(b = 500m\). Nếu muốn gặp xe với vận tốc nhỏ nhất thì người này phải chạy với vận tốc là bao nhiêu?
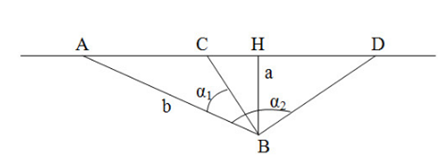
Vận tốc của xe bus: \({v_1} = 54km/h = 15m/s\)
Nếu muốn vận tốc là nhỏ nhất \( \Rightarrow \) Quãng đường đi là nhỏ nhất \( \Rightarrow \) Người đó đi theo hướng BH
Từ hình ta có: \(AH = \sqrt {{b^2} - {a^2}} = \sqrt {{{500}^2} - {{40}^2}} \approx 498,4(m)\)
Ta có: \(\dfrac{{BH}}{{{v_{\min }}}} = \dfrac{{AH}}{{{v_1}}} \to {v_{\min }} = \dfrac{{BH}}{{AH}}.{v_1} = \dfrac{{40}}{{498,4}}.15 = 1,2(m/s)\)
Một ô-tô chạy trên đường thẳng. Ở \(\dfrac{1}{3}\) đoạn đầu của đường đi, ô-tô chạy với tốc độ \(40km/h\) , ở \(\dfrac{2}{3}\) đoạn sau của đường đi, ô-tô chạy với tốc độ \(60km/h\). Tốc độ trung bình của ô-tô trên cả đoạn đường là
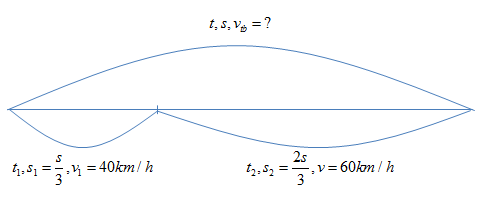
Ta có:
+ \({t_1} = \dfrac{{{s_1}}}{{{v_1}}} = \dfrac{{\dfrac{s}{3}}}{{40}} = \dfrac{s}{{120}}\)
+ \({t_2} = \dfrac{{{s_2}}}{{{v_2}}} = \dfrac{{\dfrac{{2s}}{3}}}{{60}} = \dfrac{s}{{90}}\)
Tốc độ trung bình của ô-tô trên cả đoạn đường: \({v_{tb}} = \dfrac{s}{t} = \dfrac{s}{{{t_1} + {t_2}}} = \dfrac{s}{{\dfrac{s}{{120}} + \dfrac{s}{{90}}}} = \dfrac{{360}}{7}km/h\)
Một người đi xe đạp trên một đoạn dốc thẳng MN. Trên \(\dfrac{1}{3}\) đoạn đường đi với vận tốc \(15km/h\), \(\dfrac{1}{3}\) đoạn đường tiếp theo đi với vận tốc \(10km/h\) và \(\dfrac{1}{3}\) đoạn đường cuối cùng đi với vận tốc \(5km/h\). Tính vận tốc trung bình của xe đạp trên cả đoạn đường MN.
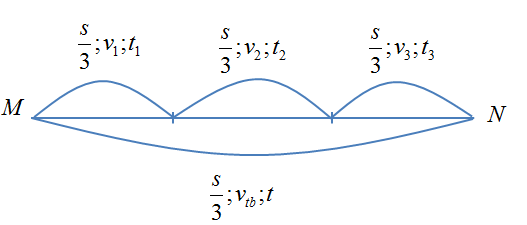
Ta có:
\({t_1} = \dfrac{{{s_1}}}{{{v_1}}} = \dfrac{{\dfrac{s}{3}}}{{15}} = \dfrac{s}{{45}}\)
\({t_2} = \dfrac{{{s_2}}}{{{v_2}}} = \dfrac{{\dfrac{s}{3}}}{{10}} = \dfrac{s}{{30}}\)
\({t_3} = \dfrac{{{s_3}}}{{{v_3}}} = \dfrac{{\dfrac{s}{3}}}{5} = \dfrac{s}{{15}}\)
Tốc độ trung bình của xe đạp trên cả quãng đường: \({v_{tb}} = \dfrac{s}{t} = \dfrac{{{s_1} + {s_2} + {s_3}}}{{{t_1} + {t_2} + {t_3}}} = \dfrac{s}{{\dfrac{s}{{45}} + \dfrac{s}{{30}} + \dfrac{s}{{15}}}} = \dfrac{{90}}{{11}} \approx 8,2km/h\)
Một máy bay cất cánh từ Hà Nội đi Bắc Kinh vào hồi \(9\) giờ \(30\) phút theo giờ Hà Nội và đến Bắc Kinh vào lúc \(14\) giờ \(30\) phút cùng ngày theo giờ địa phương. Biết giờ Bắc Kinh nhanh hơn giờ Hà Nội \(1\) giờ. Biết tốc độ trung bình của máy bay là \(1000km/h\). Coi máy bay bay theo đường thẳng. Khoảng cách từ Hà Nội đến Bắc Kinh là:
Ta có:
+ Lúc \(14h30\) ở Bắc Kinh tương ứng với \(13h30\) ở Hà Nội (do giờ Bắc Kinh nhanh hơn giờ Hà Nội \(1\) giờ)
Ta suy ra khoảng thời gian bay của máy bay: \(t = 13h30 - 9h30 = 4h\)
+ Tốc độ trung bình của máy bay: \(v = \dfrac{s}{t}\)
Suy ra, khoảng cách từ Hà Nội đến Bắc Kinh là: \(s = v.t = 1000.4 = 4000km\)
Phương trình chuyển động của các xe là:
Các đồ thị I, II, III biểu diễn tọa độ theo thời gian là những đường thẳng xiên góc, song song với nhau => Chuyển động của ba xe là thẳng đều với cùng tốc độ \(v\)
+ Xe I: xuất phát lúc \({t_0}\) tại gốc tọa độ
\( \Rightarrow \) Phương trình chuyển động của xe I: \({x_1} = v\left( {t - {t_0}} \right)\)
+ Xe II: xuất phát tại gốc tọa độ
\( \Rightarrow \) Phương trình chuyển động của xe II: \({x_2} = vt\)
+ Xe III: xuất phát tại vị trí cách gốc tọa độ một đoạn \({x_0}\)
\( \Rightarrow \) Phương trình chuyển động của xe III: \({x_3} = {x_0} + vt\)
Tìm câu sai.
A, C, D – đúng
B – sai vì: Các đồ thị I, II, III biểu diễn tọa độ theo thời gian là những đường thẳng xiên góc, song song với nhau => Chuyển động của ba xe là thẳng đều với cùng tốc độ.
Tìm câu sai.
A, C, D – đúng
B – sai vì: Các đồ thị I, II, III biểu diễn tọa độ theo thời gian là những đường thẳng xiên góc, song song với nhau => Chuyển động của ba xe là thẳng đều với cùng tốc độ.
Hai xe gặp nhau lúc mấy giờ? Nơi gặp nhau cách A bao nhiêu km?
Ta có:
+ Chọn gốc tọa độ là B, chiều dương từ B đến A, gốc thời gian lúc hai xe bắt đầu chuyển động

+ Phương trình chuyển động của mỗi xe:
- Xe tại B: \({x_B} = {x_{0B}} + {v_B}t = 0 + 40t = 40t\)
- Xe tại A: \({x_A} = {x_{0A}} + {v_A}t = AB - 80t = 150 - 80t\)
+ Hai xe gặp nhau khi \({x_A} = {x_B}\)
\(\begin{array}{l} \Leftrightarrow 150 - 80t = 40t\\ \Leftrightarrow 150 = 120t\\ \Rightarrow t = 1,25h\end{array}\)
Thay vào \({x_B}\) ta được: \({x_B} = 40.1,25 = 50km\)
Vậy 2 xe gặp nhau vào thời điểm \(\left( {8h30 + 1,25h = 9h45} \right)\) tại vị trí cách A \(\left( {AB - {x_B} = 150 - 50 = 100km} \right)\)
Phương trình chuyển động của hai xe có dạng:
Ta có:
+ Chọn gốc tọa độ là B, chiều dương từ B đến A, gốc thời gian lúc hai xe bắt đầu chuyển động

+ Phương trình chuyển động của mỗi xe:
- Xe tại B: \({x_B} = {x_{0B}} + {v_B}t = 0 + 40t = 40t\)
- Xe tại A: \({x_A} = {x_{0A}} + {v_A}t = AB - 80t = 150 - 80t\)
Phương trình chuyển động của hai xe có dạng:
Ta có:
+ Chọn gốc tọa độ là B, chiều dương từ B đến A, gốc thời gian lúc hai xe bắt đầu chuyển động

+ Phương trình chuyển động của mỗi xe:
- Xe tại B: \({x_B} = {x_{0B}} + {v_B}t = 0 + 40t = 40t\)
- Xe tại A: \({x_A} = {x_{0A}} + {v_A}t = AB - 80t = 150 - 80t\)
Chuyển động thẳng đều là:
Chuyển động thẳng đều là chuyển động thẳng, trong đó chất điểm có vận tốc tức thời không đổi.
Định nghĩa khác: Chuyển động thẳng đều là chuyển động có quỹ đạo là đường thẳng và có tốc độ trung bình như nhau trên mọi quãng đường.
Vận tốc của chất điểm trong chuyển động thẳng đều
Vận tốc của chất điểm trong chuyển động thẳng đều không thay đổi cả về dấu và độ lớn
Chuyển động thẳng đều không có đặc điểm nào dưới dây:
Trong các đặc điểm trên, chuyển động thẳng đều không có đặc điểm: Tốc độ không đổi từ lúc xuất phát đến lúc dừng lại.
Vì lúc xuất phát: vận tốc tăng, lúc dừng lại: vận tốc giảm
Chọn phát biểu sai: Chuyển động thẳng đều là chuyển động của chất điểm trên một đường thẳng và:
A - sai vì : Chuyển động thẳng đều có vận tốc không đổi: \(v=const\)
B, C, D - đúng
Chọn gốc tọa độ không trùng với vị trí ban đầu, gốc thời gian trùng với thời điểm ban đầu thì phương trình chuyển động của chất điểm chuyển động thẳng đều có dạng:
Do: Chọn gốc tọa độ không trùng với vị trí ban đầu, gốc thời gian trùng với thời điểm ban đầu
=> phương trình chuyển động của chất điểm: \(x = {x_0} + vt\)
Phương trình vận tốc của chuyển động thẳng đều:
Chuyển động thẳng đều là chuyển động thẳng, trong đó chất điểm có vận tốc tức thời không đổi.
Hay nói cách khác, vận tốc của chuyển động không đổi: \(v = c{\rm{ons}}t\)
Đồ thị vận tốc - thời gian của chuyển động thẳng đều là:
Trong chuyển động thẳng đều, vận tốc không thay đổi \(v = {v_0}\)
Suy ra: Đồ thị biểu diễn vận tốc theo thời gian là một đường thẳng song song với trục thời gian.

