Câu hỏi:
2 năm trước
Một người đi xe đạp trên một đoạn dốc thẳng MN. Trên \(\dfrac{1}{3}\) đoạn đường đi với vận tốc \(15km/h\), \(\dfrac{1}{3}\) đoạn đường tiếp theo đi với vận tốc \(10km/h\) và \(\dfrac{1}{3}\) đoạn đường cuối cùng đi với vận tốc \(5km/h\). Tính vận tốc trung bình của xe đạp trên cả đoạn đường MN.
Trả lời bởi giáo viên
Đáp án đúng: d
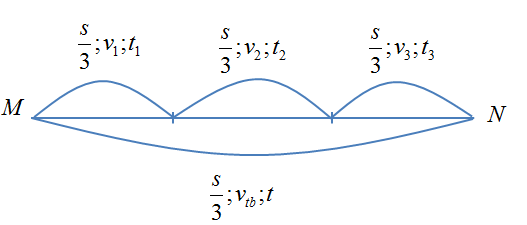
Ta có:
\({t_1} = \dfrac{{{s_1}}}{{{v_1}}} = \dfrac{{\dfrac{s}{3}}}{{15}} = \dfrac{s}{{45}}\)
\({t_2} = \dfrac{{{s_2}}}{{{v_2}}} = \dfrac{{\dfrac{s}{3}}}{{10}} = \dfrac{s}{{30}}\)
\({t_3} = \dfrac{{{s_3}}}{{{v_3}}} = \dfrac{{\dfrac{s}{3}}}{5} = \dfrac{s}{{15}}\)
Tốc độ trung bình của xe đạp trên cả quãng đường: \({v_{tb}} = \dfrac{s}{t} = \dfrac{{{s_1} + {s_2} + {s_3}}}{{{t_1} + {t_2} + {t_3}}} = \dfrac{s}{{\dfrac{s}{{45}} + \dfrac{s}{{30}} + \dfrac{s}{{15}}}} = \dfrac{{90}}{{11}} \approx 8,2km/h\)
Hướng dẫn giải:
Vận dụng biểu thức tính tốc độ trung bình: \({v_{tb}} = \dfrac{s}{t}\)
Câu hỏi khác
- Bài tập chuyển động thẳng đều lý 10 có lời giải
- Bài tập các khái niệm độ dời, quãng đường, vận tốc và gia tốc lý 10 có lời giải
- Bài tập các khái niệm cơ bản của chuyển động cơ học lý 10 có lời giải
- Bài tập chuyển động thẳng biến đổi đều lý 10 có lời giải
- Bài tập các dạng bài chuyển động thẳng biến đổi đều MÔN LÝ lớp 10
