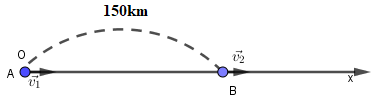
Vào lúc 14h, hai oto chuyển động thẳng đều cùng chiều đi qua các thành phố A và B cách nhau 150km. Chiều chuyển động của các xe từ A đến B. Ôtô qua thành phố A có vận tốc 75km/h. Ôtô qua thành phố B có vận tốc 50 km/h. Hai xe gặp nhau tại vị trí cách B bao nhiêu km?

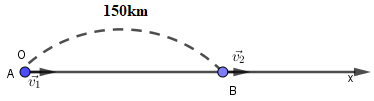
Chọn gốc tọa độ tại A, chiều dương chọn là chiều từ A hướng B. Chọn gốc thời gian là lúc 14h

Giả sử phương trình chuyển động của ô tô qua A có dạng:

\({x_A} = {x_{0A}} + {v_A}\left( {t - {t_{0A}}} \right)\)

Với: \(\left\{ \begin{array}{l}{x_{0A}} = 0\\{t_{0A}} = 0\\{v_A} = 75km/h\end{array} \right. \Rightarrow {x_A} = 0 + 75\left( {t - 0} \right) = 75t\,\,\left( {km} \right)\)

Giả sử phương trình chuyển động của ô tô qua B có dạng:

\({x_B} = {x_{0B}} + {v_B}\left( {t - {t_{0B}}} \right)\)

Với: \(\left\{ \begin{array}{l}{x_{0B}} = 150km\\{t_{0B}} = 0\\{v_B} = 50km/h\end{array} \right. \Rightarrow {x_B} = 150 + 50t\,\,\left( {km} \right)\) 

Hai xe gặp nhau khi: \({x_A} = {x_B} \Rightarrow 75t = 150 + 50t \Rightarrow t = 6h\)

Thay t = 6h vào phương trình ta có: \({x_A} = 75.6 = 450\left( {km} \right)\)

Vị trí hai xe gặp nhau cách B: \(d = 450 - 150 = 300\left( {km} \right)\)