Cho tam giác $ABC$ có \(\widehat A = {98^0},\widehat C = {57^0}\). Số đo góc B là:
Xét tam giác ABC có :$\widehat A + \widehat B + \widehat C = {180^0} \Rightarrow \widehat B = {180^0} - \left( {\widehat A + \widehat C} \right) = {180^0} - \left( {{{98}^0} + {{57}^0}} \right) = {25^0}$.
Biết $AB = 4cm,{\rm{ }}EF = 6cm,{\rm{ }}DF = 7cm.$ Tính chu vi tam giác $ABC.$
Ta có: $\Delta ABC{\rm{ }} = {\rm{ }}\Delta DEF$, suy ra: $AC = DF = 7cm,{\rm{ }}BC = EF = {\rm{ }}6cm.$
Vậy chu vi của tam giác $ABC$ là: ${C_{ABC}} = {\rm{ }}AB + AC + BC = 4 + 7 + 6 = 17cm.$
Chọn câu sai.
Ta có: $\Delta ABC{\rm{ }} = {\rm{ }}\Delta DEF$, suy ra:
- Các cạnh tương ứng bằng nhau là: \(AB = DE;\;\;AC = DF;\;\;BC = EF.\)
- Các góc tương ứng bằng nhau là: \(\widehat A = \widehat D;\;\;\widehat B = \widehat E;\;\widehat C = \widehat F.\)
Vậy A, B, D đúng, C sai.
Chọn câu sai.
Ta có: $\Delta ABC{\rm{ }} = {\rm{ }}\Delta DEF$, suy ra:
- Các cạnh tương ứng bằng nhau là: \(AB = DE;\;\;AC = DF;\;\;BC = EF.\)
- Các góc tương ứng bằng nhau là: \(\widehat A = \widehat D;\;\;\widehat B = \widehat E;\;\widehat C = \widehat F.\)
Vậy A, B, D đúng, C sai.
Tính độ dài cạnh $BC.$
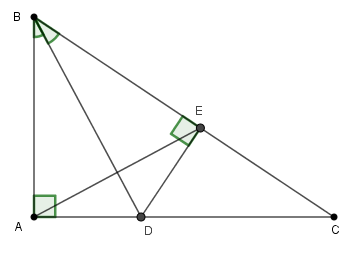
Ta có: $\widehat {EAC} + \widehat {BAE} = {90^0}$(gt)
$\widehat C + \widehat B = {90^0}$ (\(\Delta \)$ABC$ vuông tại A)
Mà $\widehat {BAE} = \widehat B = {60^0}$ ( do \(\Delta \)ABE đều) nên $\widehat {EAC} = \widehat C$
\( \Rightarrow \) \(\Delta \)AEC cân tại E
\( \Rightarrow EA = EC\) mà $EA = AB = EB = 5cm$
Do đó $EC = 5cm$
Vậy $BC = EB + EC = 5cm + 5cm = 10cm.$
Chọn câu đúng.
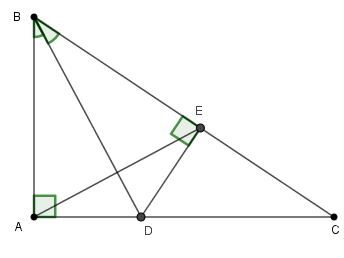
Xét $\Delta ABD$ và \(\Delta \)$EBD$ , có:
+ $\widehat {BAD} = \widehat {BED} = {90^0}(gt)$
+ BD là cạnh huyền chung
+ $\widehat {ABD} = \widehat {EBD}(gt)$
Vậy \(\Delta ABE = \Delta EBD\) (cạnh huyền – góc nhọn) nên A sai.
Ta có: \(\Delta ABE = \Delta EBD\)(cmt)\( \Rightarrow AB = EB \) (hai cạnh tương ứng).
Do đó \(\Delta \)ABE cân tại B.
Mà \(\widehat B = {60^0}\) (gt) nên \(\Delta ABE\) đều. (dhnb)
Chọn câu đúng.

Xét $\Delta ABD$ và \(\Delta \)$EBD$ , có:
+ $\widehat {BAD} = \widehat {BED} = {90^0}(gt)$
+ BD là cạnh huyền chung
+ $\widehat {ABD} = \widehat {EBD}(gt)$
Vậy \(\Delta ABE = \Delta EBD\) (cạnh huyền – góc nhọn) nên A sai.
Ta có: \(\Delta ABE = \Delta EBD\)(cmt)\( \Rightarrow AB = EB \) (hai cạnh tương ứng).
Do đó \(\Delta \)ABE cân tại B.
Mà \(\widehat B = {60^0}\) (gt) nên \(\Delta ABE\) đều. (dhnb)
Tam giác \(OBC\) là tam giác
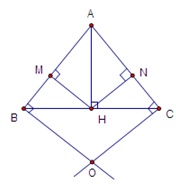
+) Ta có: \(\widehat {CBO} = {90^0} - \widehat {ABC}\) (hai góc phụ nhau)
\(\widehat {BCO} = {90^0} - \widehat {ACB}\) (hai góc phụ nhau)
Mà \(\widehat {ABC} = \widehat {ACB}\) ($\Delta ABC\;$ cân tại $A$ )
Do đó: \(\widehat {CBO} = \widehat {BCO}\) nên $\Delta OBC$ cân tại $O$ (dhnb).
Tính \(AH.\)
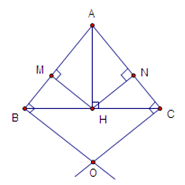
Vì tam giác \(ABC\) có \(AB = AC\) nên tam giác \(ABC\) cân tại \(A.\) Lại có \(AH\) là đường cao nên \(AH\) cũng là đường trung tuyến.
Ta có $BH = HC = $\(\dfrac{{BC}}{2} = \dfrac{{12}}{2} = 6\)cm
Xét \(\Delta AHB\) vuông tại $H,$ theo định lí Pytago ta có:
$\begin{array}{l}A{B^2} = A{H^2} + H{B^2} \Leftrightarrow {10^2} = A{H^2} + {6^2}\\ \Rightarrow A{H^2} = {10^2} - {6^2} \Leftrightarrow A{H^2} = 64\\ \Rightarrow AH = 8cm\end{array}$
Chọn câu đúng nhất.
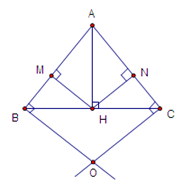
+) Xét \(\Delta AHB\) và \(\Delta AHC\) có: \(\left\{ \begin{array}{l}\widehat {AHB} = \widehat {AHC} = {90^0}\;\;\left( {gt} \right)\\AB = AC\;\;\left( {gt} \right)\\AH\;\;chung\end{array} \right.\)
Do đó \(\Delta AHB = \Delta AHC\) (cạnh huyền - cạnh góc vuông) \( \Rightarrow \widehat {BAH} = \widehat {CAH}\) (hai góc tương ứng)
\( \Rightarrow \) $AH$ là tia phân giác của góc $A$ (định nghĩa tia phân giác của một góc).
+) Xét \(\Delta BHM\)và \(\Delta CHN\) có:
\(\widehat {BMH} = \widehat {CNH} = {90^0}(gt)\)
\(\widehat B = \widehat C\) (\(\Delta ABC\) cân tại A)
$BH = HC$ \(\left( {\Delta AHB = \Delta AHC} \right)\)
Do đó \(\Delta BHM = \Delta CHN\) (cạnh huyền - góc nhọn)
Chọn câu đúng nhất.

+) Xét \(\Delta AHB\) và \(\Delta AHC\) có: \(\left\{ \begin{array}{l}\widehat {AHB} = \widehat {AHC} = {90^0}\;\;\left( {gt} \right)\\AB = AC\;\;\left( {gt} \right)\\AH\;\;chung\end{array} \right.\)
Do đó \(\Delta AHB = \Delta AHC\) (cạnh huyền - cạnh góc vuông) \( \Rightarrow \widehat {BAH} = \widehat {CAH}\) (hai góc tương ứng)
\( \Rightarrow \) $AH$ là tia phân giác của góc $A$ (định nghĩa tia phân giác của một góc).
+) Xét \(\Delta BHM\)và \(\Delta CHN\) có:
\(\widehat {BMH} = \widehat {CNH} = {90^0}(gt)\)
\(\widehat B = \widehat C\) (\(\Delta ABC\) cân tại A)
$BH = HC$ \(\left( {\Delta AHB = \Delta AHC} \right)\)
Do đó \(\Delta BHM = \Delta CHN\) (cạnh huyền - góc nhọn)
Một tam giác cân có góc ở đáy bằng \({40^0}\) thì số đo góc ở đỉnh là:
Giả sử tam giác $ABC$ cân tại $A$ ta có \(\widehat B = \widehat C\) (tính chất tam giác cân).
Theo tính chất tổng ba góc của tam giác ta có: \(\widehat A + \widehat B + \widehat C = {180^0} \Rightarrow \widehat A + 2\widehat B = {180^0}.\)
Mà \(\widehat B = \widehat C = {40^0}\;\;\left( {gt} \right) \Rightarrow \widehat A = {180^0} - 2\widehat B = {180^0} - {2.40^0} = {100^0}.\)
Cho tam giác $MNP$ có $MP = 18cm,{\rm{ }}MN = 15cm,{\rm{ }}NP = 8cm.$ Phát biểu nào sau đây đúng trong các phát biểu sau:
Ta có: \(\left\{ \begin{array}{l}M{P^2} \ne M{N^2} + N{P^2}(do\;\;{18^2} \ne {15^2} + {8^2})\\M{N^2} \ne M{P^2} + N{P^2}(do\;\;{15^2} \ne {18^2} + {8^2})\\N{P^2} \ne M{N^2} + M{P^2}(do\;\;{8^2} \ne {15^2} + {18^2})\end{array} \right.\)
Do đó tam giác $MNP$ không là tam giác vuông. Suy ra đáp án D đúng.
Cho tam giác $MNP$ và tam giác $HIK$ có: $MN = HI;{\rm{ }}PM = HK.$ Cần thêm điều kiện gì để tam giác $MNP$ và tam giác $HIK$ bằng nhau theo trường hợp cạnh – cạnh – cạnh:
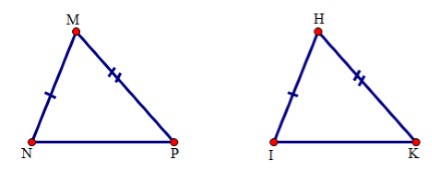
Để tam giác $MNP$ bằng tam giác $HIK$ theo trường hợp cạnh - cạnh – cạnh, mà đã có $MN = HI;{\rm{ }}PM = HK$ thì ta cần cặp cạnh còn lại của hai tam giác này bằng nhau, tức là cần thêm $NP = IK.$
Cho tam giác $DEF$ và tam giác $HKG$ có $DE = HK,$ \(\widehat E = \widehat K\), $EF = KG.$ Biết \(\widehat D = {60^0}\). Số đo góc $H$ là:
Xét tam giác $DEF$ và tam giác $HKG$ có: \(\left\{ \begin{array}{l}DE = HK\;\;\left( {gt} \right)\\\widehat E = \widehat K\;\;\;\left( {gt} \right)\\EF = KG\;\;\left( {gt} \right)\end{array} \right.\)
\( \Rightarrow \Delta DEF = \Delta HKG\;\;\left( {c - g - c} \right)\)
\( \Rightarrow \widehat H = \widehat D = {60^0}\) (hai góc tương ứng)
Cho tam giác ABC có \(\widehat A = {50^0},\widehat B = {70^0}\). Tia phân giác của góc $C$ cắt cạnh $AB$ tại $M.$ Tính số đo góc $BMC.$
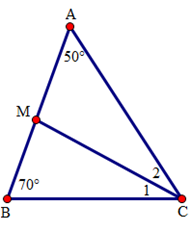
Xét tam giác $ABC$ có :$\widehat A + \widehat B + \widehat C = {180^0}$ (định lí tổng ba góc trong tam giác)
$ \Rightarrow \widehat C = {180^0} - \left( {\widehat A + \widehat B} \right) = {180^0} - \left( {{{50}^0} + {{70}^0}} \right) = {60^0}$
Vì $CM$ là tia phân giác của \(\widehat {ACB}\) nên \(\widehat {{C_1}} = \widehat {{C_2}} = \dfrac{{\widehat C}}{2} = \dfrac{{{{60}^0}}}{2} = {30^0}\).
Xét tam giác $BMC$ có: \(\widehat {BMC} = 180^\circ - \left( {\widehat B + \widehat {{C_1}}} \right)\) (định lí tổng ba góc trong tam giác)
\( \Rightarrow \widehat {BMC} = 180^\circ - \left( {70^\circ + 30^\circ } \right) = 80^\circ \)
Cho $\Delta ABC{\rm{ }} = {\rm{ }}\Delta DEF.$
Chọn câu sai.
Ta có: $\Delta ABC{\rm{ }} = {\rm{ }}\Delta DEF$, suy ra:
- Các cạnh tương ứng bằng nhau là: \(AB = DE;\;\;AC = DF;\;\;BC = EF.\)
- Các góc tương ứng bằng nhau là: \(\widehat A = \widehat D;\;\;\widehat B = \widehat E;\;\widehat C = \widehat F.\)
Vậy A, B, D đúng, C sai.
Cho $\Delta ABC{\rm{ }} = {\rm{ }}\Delta DEF.$
Biết $AB = 4cm,{\rm{ }}EF = 6cm,{\rm{ }}DF = 7cm.$ Tính chu vi tam giác $ABC.$
Ta có: $\Delta ABC{\rm{ }} = {\rm{ }}\Delta DEF$, suy ra: $AC = DF = 7cm,{\rm{ }}BC = EF = {\rm{ }}6cm.$
Vậy chu vi của tam giác $ABC$ là: ${C_{ABC}} = {\rm{ }}AB + AC + BC = 4 + 7 + 6 = 17cm.$
Cho $\Delta ABC$ vuông tại $A,$ ${\rm{ }}AH \bot BC{\rm{ }}(H \in BC);AB{\rm{ }} = 9cm,$${\rm{ }}AH = 7,2cm,{\rm{ }}HC = 9,6cm.$
Tính cạnh $AC;BC.$
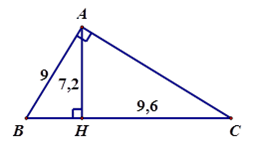
+) Xét $\Delta AHC$ vuông tại $H,$ theo định lý Py-ta-go ta có :
$\begin{array}{l}A{C^2} = A{H^2} + H{C^2}\\A{C^2} = 7,{2^2} + 9,{6^2}\\A{C^2} = 144\\ \Rightarrow AC = \sqrt {144} = 12cm\end{array}$
+) Xét \(\Delta ABC\) vuông tại $A,$ theo định lý Py-ta-go ta có:
$\begin{array}{l}B{C^2} = A{B^2} + A{C^2}\\B{C^2} = {9^2} + {12^2}\\B{C^2} = 225\\ \Rightarrow BC = \sqrt {225} = 15cm\end{array}$
Vậy \(AC = 12\,cm;BC = 15\,cm.\)
Tìm $x$ trong hình vẽ bên
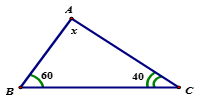
Theo định lý tổng 3 góc trong tam giác ta có: \(\widehat A + \widehat B + \widehat C = {180^0}\)
$\begin{array}{l} \Rightarrow \widehat A = 180^\circ - \left( {\widehat B + \widehat C} \right) = {180^0} - \left( {{{60}^0} + {{40}^0}} \right)\\ \Rightarrow \widehat A = {80^0}.\end{array}$

