Câu hỏi:
2 năm trước
Cho tam giác ABC có \(\widehat A = {50^0},\widehat B = {70^0}\). Tia phân giác của góc $C$ cắt cạnh $AB$ tại $M.$ Tính số đo góc $BMC.$
Trả lời bởi giáo viên
Đáp án đúng: b
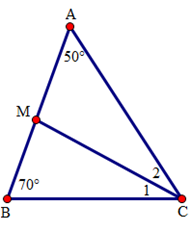
Xét tam giác $ABC$ có :$\widehat A + \widehat B + \widehat C = {180^0}$ (định lí tổng ba góc trong tam giác)
$ \Rightarrow \widehat C = {180^0} - \left( {\widehat A + \widehat B} \right) = {180^0} - \left( {{{50}^0} + {{70}^0}} \right) = {60^0}$
Vì $CM$ là tia phân giác của \(\widehat {ACB}\) nên \(\widehat {{C_1}} = \widehat {{C_2}} = \dfrac{{\widehat C}}{2} = \dfrac{{{{60}^0}}}{2} = {30^0}\).
Xét tam giác $BMC$ có: \(\widehat {BMC} = 180^\circ - \left( {\widehat B + \widehat {{C_1}}} \right)\) (định lí tổng ba góc trong tam giác)
\( \Rightarrow \widehat {BMC} = 180^\circ - \left( {70^\circ + 30^\circ } \right) = 80^\circ \)
Hướng dẫn giải:
Sử dụng tính chất tổng ba góc của một tam giác, tính chất tia phân giác của một góc, tính chất hai góc kề bù để tính số đo các góc.
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
