Trả lời bởi giáo viên
Đáp án đúng: d
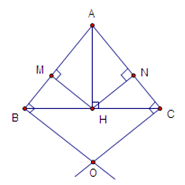
Vì tam giác \(ABC\) có \(AB = AC\) nên tam giác \(ABC\) cân tại \(A.\) Lại có \(AH\) là đường cao nên \(AH\) cũng là đường trung tuyến.
Ta có $BH = HC = $\(\dfrac{{BC}}{2} = \dfrac{{12}}{2} = 6\)cm
Xét \(\Delta AHB\) vuông tại $H,$ theo định lí Pytago ta có:
$\begin{array}{l}A{B^2} = A{H^2} + H{B^2} \Leftrightarrow {10^2} = A{H^2} + {6^2}\\ \Rightarrow A{H^2} = {10^2} - {6^2} \Leftrightarrow A{H^2} = 64\\ \Rightarrow AH = 8cm\end{array}$
Hướng dẫn giải:
Sử dụng định lí Py-ta-go trong \(\Delta AHB\) vuông tại $H$ để tính $AH.$
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
