Trả lời bởi giáo viên
Đáp án đúng: c
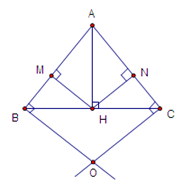
+) Xét \(\Delta AHB\) và \(\Delta AHC\) có: \(\left\{ \begin{array}{l}\widehat {AHB} = \widehat {AHC} = {90^0}\;\;\left( {gt} \right)\\AB = AC\;\;\left( {gt} \right)\\AH\;\;chung\end{array} \right.\)
Do đó \(\Delta AHB = \Delta AHC\) (cạnh huyền - cạnh góc vuông) \( \Rightarrow \widehat {BAH} = \widehat {CAH}\) (hai góc tương ứng)
\( \Rightarrow \) $AH$ là tia phân giác của góc $A$ (định nghĩa tia phân giác của một góc).
+) Xét \(\Delta BHM\)và \(\Delta CHN\) có:
\(\widehat {BMH} = \widehat {CNH} = {90^0}(gt)\)
\(\widehat B = \widehat C\) (\(\Delta ABC\) cân tại A)
$BH = HC$ \(\left( {\Delta AHB = \Delta AHC} \right)\)
Do đó \(\Delta BHM = \Delta CHN\) (cạnh huyền - góc nhọn)
Hướng dẫn giải:
+ Sử dụng trường hợp bằng nhau cạnh huyền – góc nhọn để chứng minh hai tam giác vuông \(\Delta AHB\) và \(\Delta AHC\) bằng nhau.
+ Từ hai tam giác vuông bằng nhau ta suy ra cặp góc tương ứng bằng nhau
+ Sử dụng trường hợp bằng nhau cạnh huyền – góc nhọn để chứng minh hai tam giác vuông bằng nhau
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
