Thế năng

Ta có, thế năng đàn hồi của lò xo: \({{\rm{W}}_t} = \dfrac{1}{2}k{\left( {\Delta l} \right)^2}\)

Suy ra độ cứng của lò xo: \(k = \dfrac{{2{W_t}}}{{{{\left( {\Delta l} \right)}^2}}} = \dfrac{{2.0,04}}{{{{\left( {0,02} \right)}^2}}} = 200N/m\)

Ta có, gốc thế năng tại tầng thứ mặt đất nên khoảng cách từ thang máy khi ở tầng cao nhất đến gốc là:

\(z = 60m + 40m = 100m\)

Thế năng của thang máy khi ở tầng cao nhất là: \({W_t} = mgz = 1000.9,8.10 = 980000J = 980kJ\).       

Do bỏ qua ma sát => Công tối thiểu người này cần thực hiện để lên dốc bằng công của trọng lực

\({A_P} = mgh\)

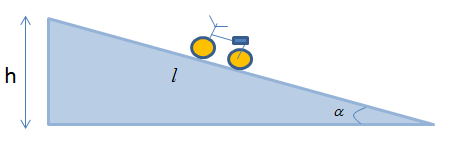
+ Khi dốc nghiêng góc \({\alpha _1} = {20^0}\), ta có công: \({A_1} = mg{h_1} = mg{l_1}{\rm{sin}}{\alpha _1}\)

+ Khi dốc nghiêng góc \({\alpha _2} = {30^0}\), ta có công: \({A_2} = mg{h_2} = mg{l_2}{\rm{sin}}{\alpha _2}\)

Theo đề bài ta có,  \({A_1} = {A_2} \Leftrightarrow mg{l_1}{\rm{sin}}{\alpha _1} = mg{l_2}\sin {\alpha _2}\)

Ta suy ra quãng đường xe đi được khi góc nghiêng \({\alpha _2}\) là: \({l_2} = \dfrac{{{l_1}{\rm{sin}}{\alpha _1}}}{{{\rm{sin}}{\alpha _2}}} = \dfrac{{40.\sin {\rm{2}}{{\rm{0}}^0}}}{{{\rm{sin3}}{{\rm{0}}^0}}} \approx 27,4m\) 

Công suất \(P = \dfrac{{{A_P}}}{t} = \dfrac{{mgh}}{t} = \dfrac{m}{t}gh\)

Ta có \(\dfrac{m}{t} = {10^4}kg\)

Suy ra công suất: \(P = {10^4}.10.30 = {3.10^6}{\rm{W}} = 3MW\)  

Nếu chọn gốc thế năng là mặt đất thì công thức tính thế năng trọng trường của một vật ở độ cao h là:

\({{\rm{W}}_t} = mgh\)

A, C, D – đúng

B – sai vì : thời gian rơi phụ thuộc vào gia tốc rơi tự do và vận tốc ban đầu theo phương thẳng đứng. Ở đây vận tốc ban đầu như nhau nhưng đường đi khác nhau nên vận tốc ban đầu theo phương thẳng đứng khác nhau.

Ta có :

Khi một vật được ném lên, độ cao của vật tăng dần nên thế năng tăng.

Trong quá trình chuyển động của vật từ dưới lên, trọng lực luôn hướng ngược chiều chuyển động nên nó là lực cản, do đó trọng lực sinh công âm.

Công thức tính thế năng đàn hồi của lò xo:

\({{\rm{W}}_t} = \frac{1}{2}k{\left( {\Delta l} \right)^2}\)  trong đó \(\Delta l\): độ biến dạng của lò xo

Ta có, thế năng hấp dẫn là đại lượng vô hướng, có thể âm, dương hoặc bằng 0

Thế năng đàn hồi và thế năng hấp dẫn đều là đại lượng vô hướng

+ Thế năng hấp dẫn có thể dương, âm hoặc bằng 0 

+ Thế năng đàn hồi luôn lớn hơn hoặc bằng 0

=> Phương án D - sai

Công thức tính thế năng đàn hồi của lò xo:

\({{\rm{W}}_t} = \dfrac{1}{2}k{\left( {\Delta l} \right)^2}\)  trong đó \(\Delta l\): độ biến dạng của lò xo.

Theo định luật Húc: \({F_{dh}} = k.\left( {\Delta l} \right) \Rightarrow k = \dfrac{F}{{\Delta l}} = \dfrac{5}{{0,02}} = 250N/m\).

Công của ngoại lực tác dụng để lò xo giãn ra \(5 cm\) là: \(A = {W_t} = \dfrac{1}{2}k{x^2} = \dfrac{1}{2}.250.{\left( {0,05} \right)^2} = 0,3125J\)\( \approx 0,31J\).

Đại lượng phụ thuộc vào vị trí của vật trong trọng trường là thế năng

Khi vật chuyển động theo phương ngang thì vị trí trọng trường của vật không đổi => thế năng không đổi 

Ta có:     \({W_t} = \frac{1}{2}k{\left( {\Delta l} \right)^2} = \frac{1}{2}100{\left( {0,05} \right)^2} = 0,125J.\)

Ta có:   \({W_t} = \dfrac{1}{2}k{\left( {\Delta l} \right)^2} \Rightarrow k = \dfrac{{2{W_t}}}{{{{\left( {\Delta l} \right)}^2}}} = \dfrac{{2.0,2}}{{{{\left( {0.04} \right)}^2}}} = 250N/m\).

Ta có:

Thế năng của vật 1 có giá trị là: \({W_{t1}} = m.g.2.h = 2mgh\)  (1).

Thế năng của vật 2 có giá trị là: \({W_{t2}} = 2.m.g.h = 2mgh\) (2).

=> Thế năng vật 1 bằng thế năng vật 2

Ta có gốc thế năng tại tầng thứ 10 nên khoảng cách từ thang máy khi ở tầng cao nhất đến gốc là: z =100 – 40 = 60m.

Thế năng của thang máy là: \({W_t} = mgz = 1000.9,8.60 = 588kJ\).                                                                                                          

Chọn mốc thế năng tại mặt đất

+ Tại vị trí xuất phát, cáp treo có độ cao \({z_1} = 10m\)

+ Tại trạm thứ nhất, cáp treo có độ cao \({z_2} = 550m\)

Công của trọng lực bằng độ giảm thế năng:

\(\begin{array}{l}{A_P} = {{\rm{W}}_{{t_1}}} - {{\rm{W}}_{{t_2}}} = mg{z_1} - mg{z_2}\\ = mg\left( {{z_1} - {z_2}} \right)\\ = 800.10\left( {10 - 550} \right)\\ =  - 4320000J =  - {432.10^4}J\end{array}\)

Ta có:

+ Biến thiên thế năng chính bằng công của trọng lực: \({{\rm{W}}_{{t_1}}} - {{\rm{W}}_{{t_2}}} = {A_P}\) (1)

+ \(\overrightarrow P \) hợp với phương rơi một góc \(\alpha  = {0^0}\)

Ta suy ra công của trọng lực: \({A_P} = P.h = mgh\)  (2)

Từ (1) và (2), ta suy ra: \({{\rm{W}}_{{t_1}}} - {{\rm{W}}_{{t_2}}} = mgh\)

\( \Rightarrow h = \dfrac{{{{\rm{W}}_{{t_1}}} - {{\rm{W}}_{{t_2}}}}}{{mg}} = \dfrac{{500 - \left( { - 900} \right)}}{{2.10}} = 70m\)

Vậy so với mặt đất, vật đã rơi từ độ cao \(h = 70m\)