Một thang máy có khối lượng 1,5 tấn chuyển động từ tầng cao nhất cách mặt đất 120m xuống tầng thứ 10 cách mặt đất 40m. Nếu chọn gốc thế năng tại tầng 10, lấy g = 9,8m/s2. Thế năng của thang máy ở tầng cao nhất là:
Chọn gốc thế năng tại tầng 10.
Khoảng cách từ tầng cao nhất đến gốc thế năng là:
\(z = 120 - 40 = 80m\)
Thế năng của thang máy ở tầng cao nhất là:
\({{\rm{W}}_t} = mgz = 1,5.1000.9,8.80 = 1\,176\,000J = 1\,176kJ\)
Khi nị nén 3cm, một lò xo có thế năng đàn hồi bằng 0,18J. Độ cứng của lò xo bằng
Ta có:
\({{\rm{W}}_{dh}} = \dfrac{1}{2}k.\Delta {l^2} \Rightarrow k = \dfrac{{2.{{\rm{W}}_{dh}}}}{{\Delta {l^2}}} = \dfrac{{2.0,18}}{{0,{{03}^2}}} = 400N/m\)
Một lò xo có độ cứng \(100N/m\), một đầu cố định, đầu kia gắn với vật nhỏ. Khi lò xo bị nén \(4cm\) thì thế năng đàn hồi của hệ là
Thế năng đàn hồi của hệ khi lò xo bị nén 4cm là:
\({W_t} = \frac{1}{2}.k{\left( {\Delta l} \right)^2} = \frac{1}{2}.100.0,042 = 0,08J\)
Một vật khối lượng m ở nơi có gia tốc trọng trường \(g\). Khi vật ở độ cao \(z\) so với mốc thế năng thì thế năng trọng trường của vật có biểu thức là:
Một vật khối lượng m ở nơi có gia tốc trọng trường \(g\). Khi vật ở độ cao \(z\) so với mốc thế năng thì thế năng trọng trường của vật có biểu thức là: \({W_t} = mgz\)
Chọn gốc thế năng tại mặt đất. Thế năng của vật nặng \(2kg\) ở dưới đáy một giếng sâu \(10m\) tại nơi có gia tốc trọng trường \(g = 10m/{s^2}\) là
Chọn gốc thế năng tại mặt đất.
Đáy giếng sâu 10m có \(z = - 10m\)
Thế năng của vật tại đáy giếng:
\({W_t} = mgz = 2.10.\left( { - 10} \right) = - 200J\)
Cho một lò xo đàn hồi nằm ngang ở trạng thái ban đầu không bị biến dạng. Khi tác dụng một lực \(F = 3N\) kéo lò xo theo phương ngang ta thấy nó giãn được \(2cm\). Tính giá trị thế năng đàn hồi của lò xo khi đó:
Độ cứng của lò xo:
\(k = \dfrac{{{F_{dh}}}}{{\Delta l}} = \dfrac{3}{{0,02}} = 150N/m\)
Thế năng đàn hồi của lò xo:
\({{\rm{W}}_t} = \dfrac{{k.\Delta {l^2}}}{2} = \dfrac{{150.0,{{02}^2}}}{2} = 0,03J\)
Lò xo có độ cứng k = 200Nm, một đầu cố định đầu kia gắn với vật nhỏ có khối lượng 500g. Khi bị lo xo nén 4cm thì thế năng đàn hồi của hệ bằng bao nhiêu?
Ta có: \(\left\{ \begin{array}{l}k = 200N/m\\\Delta l = 4cm = 0,04m\end{array} \right.\)
Thế năng đàn hồi của hệ là: \({{\rm{W}}_t} = \dfrac{1}{2}{k^2}.\Delta l = \dfrac{1}{2}.200.0,{04^2} = 0,16J\)
Cho một lò xo đàn hồi nằm ngang ở trạng thái ban đầu không biến dạng, tác dụng một lực F = 3N kéo lò xo theo phương ngang nó dãn 2cm. Công do lực đàn hồi thực hiện khi lò xo được kéo dãn thêm từ 2cm đến 3,5cm là:
Khi tác dụng lực 3N lò xo dãn ra 2cm = 0,02m. Ta có:
3 = 0,02k => k = 150 N/m
Công lực đàn hồi thực hiện khi lò xo dãn thêm từ 2cm = 0,02m đển 3,5cm = 0,035m là:
A = 0,5k(0,0352 – 0,022 ) = 0,062J
Chọn phương án đúng.
Khi một vật từ độ cao z, với cùng vận tốc ban đầu, bay xuống đất theo những con đường khác nhau thì:
A – sai vì : Vật bay xuống đất theo những con đường khác nhau => quỹ đạo rơi khác nhau
B – sai vì : thời gian rơi phụ thuộc vào gia tốc rơi tự do và vận tốc ban đầu theo phương thẳng đứng. Ở đây vận tốc ban đầu như nhau nhưng đường đi khác nhau nên vận tốc ban đầu theo phương thẳng đứng khác nhau.
C – sai vì: Công của trọng lực là như nhau \({A_P} = P.z\)
D – đúng
Một con lắc đơn dao động xung quanh vị trí cân bằng B. Chọn mốc thế năng tại B. Khi con lắc di chuyển từ A đến C thì:
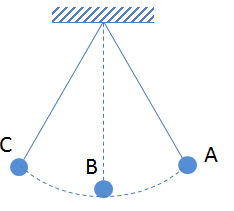

Ta có,
+ Khi con lắc di chuyển từ A => B: độ cao của vật so với mốc giảm => Thế năng giảm
+ Khi con lắc di chuyển từ B => C: độ cao của vật so với mốc tăng => Thế năng tăng
=> Khi con lắc di chuyển từ A đến C thì: Thế năng giảm rồi tăng
Thế năng đàn hồi là đại lượng:
Ta có, biểu thức tính thế năng đàn hồi: \({{\rm{W}}_t} = \dfrac{1}{2}k{\left( {\Delta l} \right)^2}\)
=> Thế năng đàn hồi là đại lượng vô hướng, luôn dương hoặc bằng 0
Phát biểu nào sau đây đúng: Thế năng hấp dẫn và thế năng đàn hồi
A - đúng
B – sai vì: Thế năng hấp dẫn \({{\rm{W}}_t} = mgz\), thế năng đàn hồi \({{\rm{W}}_t} = \dfrac{1}{2}k{\left( {\Delta l} \right)^2}\)
C – sai vì: Thế năng đàn hồi và thế năng hấp dẫn đều phụ thuộc vào điểm đầu và điểm cuối
D – sai vì: Thế năng đàn hồi luôn dương hoặc bằng 0 mà không có giá trị âm
Thế năng của một lò xo khi nó bị dãn một khoảng \(x\) là \({{\rm{W}}_t} = k{x^2}\), với \(k\) là hằng số. Lực đàn hồi khi đó bằng
+ Gọi \({k_1}\) - độ cứng của lò xo
Ta có, thế năng đàn hồi của lò xo khi dãn một khoảng \(x\) là: \({{\rm{W}}_t} = \dfrac{1}{2}{k_1}{x^2}\)
Theo đề bài ta có:
\(\begin{array}{l}{{\rm{W}}_t} = k{x^2}\\ \Rightarrow \dfrac{1}{2}{k_1}{x^2} = k{x^2}\\ \Rightarrow {k_1} = 2k\end{array}\)
+ Lực đàn hồi của lò xo dãn một khoảng \(x\) là: \({F_{dh}} = \left| {{k_1}x} \right| = 2kx\)
Thế năng đàn hồi của một lò xo không phụ thuộc vào:
Ta có, thế năng đàn hồi \({{\rm{W}}_t} = \dfrac{1}{2}k{\left( {\Delta l} \right)^2}\)
=> Thế năng đàn hồi không phụ thuộc vào chiều biến dạng của lò xo
Một người kéo một lực kế, số chỉ của lực kế là \(400N\), độ cứng của lò xo lực kế là \(1000N/m\). Công do người thực hiện bằng
Ta có:
+ Lực đàn hồi cũng chính là số chỉ của lực kế: \(F = \left| {k\Delta l} \right| = 400N\)
=> Độ biến dạng của lò xo so với vị trí ban đầu: \(\Delta l = \dfrac{F}{k} = \dfrac{{400}}{{1000}} = 0,4m\)
+ Chọn mốc thế năng tại vị trí ban đầu (lò xo không dãn – không nén)
=> Công do người thực hiện chính bằng thế năng đàn hồi của lò xo: \(A = {{\rm{W}}_t} = \dfrac{1}{2}k{\left( {\Delta l} \right)^2} = \dfrac{1}{2}.1000.0,{4^2} = 80J\)
Chỉ ra câu sai trong các phát biểu sau:
A, B, D – đúng
C – sai vì: Không phải lúc nào công của trọng lực cũng luôn dương
Một vật nằm yên có thể có
Ta có, một vật nằm yên => Vận tốc của vật \(v = 0m/s\)
=> Một vật nằm yên có thể có thế năng (không thể có vận tốc, động lượng hay động năng vì vận tốc của vật bằng 0)
Một viên đạn được bắn từ mặt đất lên cao hợp với phương ngang góc \(\alpha \), vận tốc đầu \(\overrightarrow {{v_0}} \). Bỏ qua lực cản môi trường. Đại lượng không đổi khi viên đạn đang bay là
Khi viên đạn đang bay thì:
+ Thế năng, động năng và động lượng của vật thay đổi
+ Gia tốc của vật không đổi vì: \(\overrightarrow a = \overrightarrow g \)
Một lò xo có độ cứng \(k = 200N/m\), bị nén ngắn lại \(10cm\) so với chiều dài tự nhiên ban đầu. Chọn mốc thế năng tại vị trí ban đầu. Thế năng đàn hồi của lò xo là
Ta có độ biến dạng của lò xo so với vị trí ban đầu: \(\Delta l = 10cm = 0,1m\)
=> Thế năng đàn hồi của lò xo tại vị trí đó: \({{\rm{W}}_t} = \dfrac{1}{2}k{\left( {\Delta l} \right)^2} = \dfrac{1}{2}.200.{\left( {0,1} \right)^2} = 1J\)
Cho một lò xo đàn hồi nằm ngang ở trạng thái ban đầu không bị biến dạng. Khi tác dụng một lực \(3N\) kéo lò xo theo phương ngang ta thấy nó dãn được \(2cm\). Thế năng đàn hồi của lò xo có giá trị bằng
+ Ta có độ biến dạng của lò xo so với vị trí ban đầu: \(\Delta l = 2cm = 0,02m\)
Lực đàn hồi của lò xo khi đó: \({F_{dh}} = \left| {k\Delta l} \right|\)
Ta suy ra độ cứng của lò xo: \(k = \dfrac{{{F_{dh}}}}{{\left| {\Delta l} \right|}} = \dfrac{3}{{0,02}} = 150N/m\)
=> Thế năng đàn hồi của lò xo tại vị trí đó: \({{\rm{W}}_t} = \dfrac{1}{2}k{\left( {\Delta l} \right)^2} = \dfrac{1}{2}.150.{\left( {0,02} \right)^2} = 0,03J\)

