Câu hỏi:
2 năm trước
Một người thực hiện một công đạp xe lên đoạn đường dài \(40m\) trên một dốc nghiêng \({20^0}\) so với phương ngang. Bỏ qua ma sát. Nếu thực hiện một công cũng như vậy mà lên dốc nghiêng \({30^0}\) so với phương ngang thì sẽ đi được đoạn đường dài
Trả lời bởi giáo viên
Đáp án đúng: b
Do bỏ qua ma sát => Công tối thiểu người này cần thực hiện để lên dốc bằng công của trọng lực
\({A_P} = mgh\)
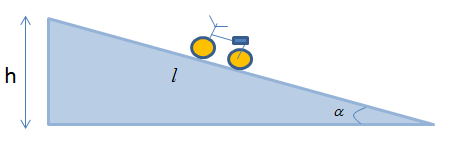
+ Khi dốc nghiêng góc \({\alpha _1} = {20^0}\), ta có công: \({A_1} = mg{h_1} = mg{l_1}{\rm{sin}}{\alpha _1}\)
+ Khi dốc nghiêng góc \({\alpha _2} = {30^0}\), ta có công: \({A_2} = mg{h_2} = mg{l_2}{\rm{sin}}{\alpha _2}\)
Theo đề bài ta có, \({A_1} = {A_2} \Leftrightarrow mg{l_1}{\rm{sin}}{\alpha _1} = mg{l_2}\sin {\alpha _2}\)
Ta suy ra quãng đường xe đi được khi góc nghiêng \({\alpha _2}\) là: \({l_2} = \dfrac{{{l_1}{\rm{sin}}{\alpha _1}}}{{{\rm{sin}}{\alpha _2}}} = \dfrac{{40.\sin {\rm{2}}{{\rm{0}}^0}}}{{{\rm{sin3}}{{\rm{0}}^0}}} \approx 27,4m\)
Hướng dẫn giải:
Sử dụng biểu thức tính thế năng: \({{\rm{W}}_t} = mgz\)
