Cho một lò xo nằm ngang ở trạng thái ban đầu không bị biến dạng. Khi tác dụng một lực F = 4N kéo lò xo cũng theo phương ngang, ta thấy nó dãn ra được 2cm. Tìm độ cứng của lò xo và thế năng đàn hồi của lò xo khi nó dãn ra được 3cm là:
Lực đàn hồi: \({F_{dh}} = k.\left| {\Delta l} \right|\)
Có: \(\left\{ \begin{array}{l}{F_{dh}} = 4N\\\Delta l = 2cm = 0,02m\end{array} \right.\)
Độ cứng: \(k = \dfrac{{{F_{dh}}}}{{\left| {\Delta l} \right|}} = \dfrac{4}{{0,02}} = 200N/m\)
Thế năng đàn hồi của lò xo khi nó dãn ra được 3cm là:
\({{\rm{W}}_{dh}} = \dfrac{1}{2}k.\Delta l{'^2} = \dfrac{1}{2}.200.0,{03^2} = 0,09J\)
Một cần cẩu nâng một contenơ có khối lượng 3200kg từ mặt đất lên độ cao 3m (tính theo di chuyển của trọng tâm của contenơ), sau đó đổi hướng và hạ nó xuống sàn một ô tô tải ở độ cao cách mặt đất 1,5m. Lấy g = 10m/s2. Thế năng của contenơ trong trọng trường khi nó ở độ cao 3m và công của lực phát động (lực căng của dây cáp) để nâng nó lên độ cao này là bao nhiêu, coi chuyển động là đều.

Chọn mốc thế năng tại mặt đất.
Thế năng của contenơ trong trọng trường khi nó ở độ cao 3m là:
\({{\rm{W}}_t} = mgz = 3200.10.3 = 96000J\)
Coi chuyển động là đều thì công của lực phát động bằng độ lớn công cản (công của trọng lực) nên ta có:
\({{\rm{A}}_{\overrightarrow F }}{\rm{ = }}\left| {{{\rm{A}}_{\overrightarrow P }}} \right| = \Delta {{\rm{W}}_t} = {{\rm{W}}_t} - {{\rm{W}}_{t0}} = 96000 - 0 = 96000J\)
Trong công viên giải trí, một xe có khối lượng m = 100kg chạy trên đường ray có mặt cắt như hình vẽ. Độ cao của các điểm A, B, C, D, E được tính đối với mặt đất và có các giá trị: \({z_A}\; = 20m;{z_B}\; = 10m;{z_C}\; = 15m;{z_D}\; = 5m;{z_E}\; = 18m\). Lấy g = 10m/s2. Độ biến thiên thế năng của xe trong trọng trường khi nó di chuyển từ A đến B; từ B đến C; từ A đến D; từ A đến E có giá trị lần lượt là:
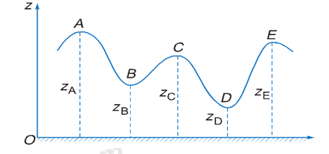
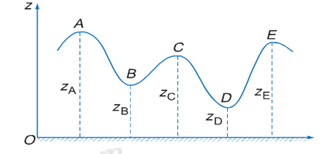
Ta có: \(\left\{ \begin{array}{l}m = 100kg\\{z_A}\; = 20m;{z_B}\; = 10m;{z_C}\; = 15m;{z_D}\; = 5m;{z_E}\; = 18m\\g = 10m/{s^2}\end{array} \right.\)
Độ biến thiên thế năng của xe trong trọng trường khi nó di chuyển từ A đến B:
\(\begin{array}{l}\Delta {{\rm{W}}_{tAB}} = {{\rm{W}}_{tA}} - {{\rm{W}}_{tB}} = mg{z_A} - mg{z_B} = mg\left( {{z_A} - {z_B}} \right)\\ \Rightarrow \Delta {{\rm{W}}_{tAB}} = 100.10.\left( {20 - 10} \right) = 10000J\end{array}\)
Độ biến thiên thế năng của xe trong trọng trường khi nó di chuyển từ B đến C:
\(\begin{array}{l}\Delta {{\rm{W}}_{tBC}} = {{\rm{W}}_{tB}} - {{\rm{W}}_{tC}} = mg{z_B} - mg{z_C} = mg\left( {{z_B} - {z_C}} \right)\\ \Rightarrow \Delta {{\rm{W}}_{tBC}} = 100.10.\left( {10 - 15} \right) = - 5000J\end{array}\)
Độ biến thiên thế năng của xe trong trọng trường khi nó di chuyển từ A đến D:
\(\begin{array}{l}\Delta {{\rm{W}}_{tAD}} = {{\rm{W}}_{tA}} - {{\rm{W}}_{tD}} = mg{z_A} - mg{z_D} = mg\left( {{z_A} - {z_D}} \right)\\ \Rightarrow \Delta {{\rm{W}}_{tAD}} = 100.10.\left( {20 - 5} \right) = 15000J\end{array}\)
Độ biến thiên thế năng của xe trong trọng trường khi nó di chuyển từ A đến E:
\(\begin{array}{l}\Delta {{\rm{W}}_{tAE}} = {{\rm{W}}_{tA}} - {{\rm{W}}_{tE}} = mg{z_A} - mg{z_E} = mg\left( {{z_A} - {z_E}} \right)\\ \Rightarrow \Delta {{\rm{W}}_{tAE}} = 100.10.\left( {20 - 18} \right) = 2000J\end{array}\)
Một lò xo có độ cứng \(k = 40N/m\), chọn mốc thế năng ở vị trí lò xo không biến dạng thì khi lò xo dãn \(3cm\) thế năng đàn hồi của lò xo bằng
Chọn mốc thế năng tại vị trí lò xo không biến dạng.
Độ biến dạng của lò xo: \(\Delta l = 3cm = 0,03m\)
Thế năng đàn hồi của lò xo bằng:
\({W_t} = \dfrac{1}{2}k.{\left( {\Delta l} \right)^2} = \dfrac{1}{2}.40.0,{03^2} = 0,018J\)

