Gọi $x_1, x_2$ là các nghiệm của phương trình ${\left( {{{\log }_{\frac{1}{3}}}x} \right)^2} - \left( {\sqrt 3 + 1} \right){\log _3}x + \sqrt 3 = 0$. Khi đó tích $x_1, x_2$ bằng:
${\left( {{{\log }_{\frac{1}{3}}}x} \right)^2} - \left( {\sqrt 3 + 1} \right){\log _3}x + \sqrt 3 = 0$ điều kiện của phương trình là $x > 0$
$ \Leftrightarrow {\left( {{{\log }_3}x} \right)^2} - \left( {\sqrt 3 + 1} \right){\log _3}x + \sqrt 3 = 0$
Đặt $t = \log_{3}x$ , phương trình trở thành:
${t^2} - \left( {\sqrt 3 + 1} \right)t + \sqrt 3 = 0 \Rightarrow \left[ \begin{array}{l}t = 1\\t = \sqrt 3 \end{array} \right.$
$ \Rightarrow \left[ \begin{array}{l}{\log _3}x = 1\\{\log _3}x = \sqrt 3 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = {3^{\sqrt 3 }}\end{array} \right. \Rightarrow {x_1}.{x_2} = {3.3^{\sqrt 3 }} = {3^{\sqrt 3 + 1}}$
Tìm $m$ để phương trình $m\ln \left( {1 - x} \right) - \ln x = m$ có nghiệm \(x \in (0;1)\)
+ Cô lập \(m : m(\ln (1 - x) - 1) = \ln x \Rightarrow m = \dfrac{{\ln x}}{{\ln (1 - x) - 1}}\) với $1 > x > 0$ .
+ Nhận xét đáp án: ta thấy \(\dfrac{{\ln x}}{{\ln (1 - x) - 1}} > 0{\rm{ }},\forall 0 < x < 1\). Loại C và D
+ Tính giới hạn của \(y =\dfrac{{\ln x}}{{\ln (1 - x) - 1}}\) khi $x$ tiến dần tới $1$ thì thấy $y$ dần tiến tới $0$ . Loại B.
Giả sử $m$ là số thực sao cho phương trình \(\log _3^2x - (m + 2){\log _3}x + 3m - 2 = 0\) có hai nghiệm \({x_1},{x_2}\) phân biệt thỏa mãn \({x_1}.{x_2} = 9\) .
Khi đó $m$ thỏa mãn tính chất nào sau đây?
Đặt \(t = {\log _3}x\) suy ra phương trình trở thành \({t^2} - (m + 2)t + 3m - 2 = 0\)(*).
Để phương trình có hai nghiệm \({x_1};{x_2}\) thì (*) cũng có hai nghiệm \({t_1};{t_2}\) .
Phương trình (*) có 2 nghiệm phân biệt \({t_1};{t_2}\)
$ \Leftrightarrow \Delta > 0\, \Leftrightarrow \,{\left( {m + 2} \right)^2} - 4\left( {3m - 2} \right) > 0\, \Leftrightarrow \left[ \begin{array}{l}m > 6\\m < 2\end{array} \right.$.
Ta có: $\left\{ \begin{array}{l}{x_1} = {3^{{t_1}}}\\{x_2} = {3^{{t_2}}}\end{array} \right. \Rightarrow {x_1}.{x_2} = {3^{{t_1} + {t_2}}} = 9 \Leftrightarrow {t_1} + {t_2} = 2.$
Theo hệ thức Vi-ét ta có: \({t_1} + {t_2} = m + 2\)
\( \Rightarrow m + 2 = 2 \Leftrightarrow m = 0\).
Suy ra \(m \in \left( { - 1;1} \right)\)
Cho \(x,\,\,y\) là các số thực dương thỏa mãn \({\log _2}\dfrac{{3x + 3y + 4}}{{{x^2} + {y^2}}}\) \( = \left( {x + y - 1} \right)\left( {2x + 2y - 1} \right) - 4\left( {xy + 1} \right)\). Giá trị lớn nhất của biểu thức \(P = \dfrac{{5x + 3y - 2}}{{2x + y + 1}}\) bằng:
Ta có:
\(\begin{array}{l}\,\,\,\,\,{\log _2}\dfrac{{3x + 3y + 4}}{{{x^2} + {y^2}}} = \left( {x + y - 1} \right)\left( {2x + 2y - 1} \right) - 4\left( {xy + 1} \right)\\ \Leftrightarrow {\log _2}\left( {3x + 3y + 4} \right) - {\log _2}\left( {{x^2} + {y^2}} \right) = \left( {x + y - 1} \right)\left[ {2\left( {x + y} \right) - 1} \right] - 4\left( {xy + 1} \right)\\ \Leftrightarrow {\log _2}\left( {3x + 3y + 4} \right) - {\log _2}\left( {{x^2} + {y^2}} \right) = 2{\left( {x + y} \right)^2} - 3\left( {x + y} \right) + 1 - 4\left( {xy + 1} \right)\\ \Leftrightarrow {\log _2}\left( {3x + 3y + 4} \right) - {\log _2}\left( {{x^2} + {y^2}} \right) = 2\left( {{x^2} + {y^2}} \right) + 4xy - \left( {3x + 3y} \right) + 1 - 4xy - 4\\ \Leftrightarrow {\log _2}\left( {3x + 3y + 4} \right) - {\log _2}\left( {{x^2} + {y^2}} \right) = 2\left( {{x^2} + {y^2}} \right) - \left( {3x + 3y + 4} \right) + 1\\ \Leftrightarrow {\log _2}\left( {3x + 3y + 4} \right) + \left( {3x + 3y + 4} \right) = {\log _2}\left( {{x^2} + {y^2}} \right) + 2\left( {{x^2} + {y^2}} \right) + {\log _2}2\\ \Leftrightarrow {\log _2}\left( {3x + 3y + 4} \right) + \left( {3x + 3y + 4} \right) = {\log _2}\left( {2{x^2} + 2{y^2}} \right) + \left( {2{x^2} + 2{y^2}} \right)\,\,\,\left( * \right)\end{array}\)
Xét hàm số đặc trưng \(f\left( t \right) = {\log _2}t + t\,\,\left( {t > 0} \right)\) ta có \(f'\left( t \right) = \dfrac{1}{{t\ln 2}} + 1 > 0\,\,\forall t > 0\).
\( \Rightarrow \) Hàm số \(y = f\left( t \right)\) luôn đồng biến trên \(\left( {0; + \infty } \right)\).
Do đó \(\left( * \right) \Leftrightarrow 3x + 3y + 4 = 2{x^2} + 2{y^2}\).
Ta có: \({\left( {x + y} \right)^2} \le 2\left( {{x^2} + {y^2}} \right) = 3x + 3y + 4\).
\( \Leftrightarrow {\left( {x + y} \right)^2} - 3\left( {x + y} \right) - 4 \le 0 \Leftrightarrow - 1 \le x + y \le 4\).
Kết hợp điều kiện đề bài ta có \(0 < x + y \le 4\).
Xét biểu thức \(P = \dfrac{{5x + 3y - 2}}{{2x + y + 1}} = \dfrac{{2\left( {2x + y + 1} \right) + x + y - 4}}{{2x + y + 1}} = 2 + \dfrac{{x + y - 4}}{{2x + y + 1}}\).
Do \(x + y \le 4 \Leftrightarrow x + y - 4 \le 0 \Leftrightarrow \dfrac{{x + y - 4}}{{2x + y + 1}} \le 0\) \( \Rightarrow P \le 2\).
Vậy \({P_{\max }} = 2 \Leftrightarrow \left\{ \begin{array}{l}x + y = 4\\x = y\end{array} \right. \Leftrightarrow x = y = 2\).
Số nghiệm của phương trình ${\log _3}\left| {{x^2} - \sqrt 2 x} \right| = {\log _5}\left( {{x^2} - \sqrt 2 x + 2} \right)$là
Đặt ${x^2} - \sqrt 2 x = t$ khi đó ${\log _3}|t| = {\log _5}(t + 2)(t > - 2;t \ne 0)$
Đặt ${\log _3}|t| = {\log _5}(t + 2) = a \Rightarrow \left\{ \begin{array}{l}|t| = {3^a}\\t + 2 = {5^a}\end{array} \right. $
$\Rightarrow \left| {{5^a} - 2} \right| = {3^a} \Leftrightarrow \left[ \begin{array}{l}{5^a} - 2 = - {3^a}\\{5^a} - 2 = {3^a}\end{array} \right. \Rightarrow \left[ \begin{array}{l}{5^a} + {3^a} = 2(1)\\{5^a} = {3^a} + 2(2)\end{array} \right.$
Xét (1): $f(a) = {5^a} + {3^a} \Rightarrow f'(a) = {5^a}\ln 5 + {3^a}\ln 3 > 0(\forall a \in R)$ nên hàm số đồng biến trên $R$
Mặt khác $f(0) = 2$ do đó phương trình $f(a) = f(0)$ có 1 nghiệm duy nhất $a = 0 \Rightarrow t = -1$
Suy ra: ${x^2} - \sqrt 2 x + 1 = 0$ (vô nghiệm)
Xét (2) $ \Leftrightarrow {\left( {\dfrac{3}{5}} \right)^a} + 2.{\left( {\dfrac{1}{5}} \right)^a} = 1$.
Đặt $g(a) = {\left( {\dfrac{3}{5}} \right)^a} + 2.{\left( {\dfrac{1}{5}} \right)^a} \Rightarrow g'(a) = {\left( {\dfrac{3}{5}} \right)^a}\ln \dfrac{3}{5} + 2.{\left( {\dfrac{1}{5}} \right)^a}\ln \dfrac{1}{5} < 0(\forall a \in R)$
Nên hàm số $g(a)$ nghịch biến trên $R$ do đó phương trình $g(a) = 1$ có tối đa 1 nghiệm.
Mà $g(a) = g(1)$ nên $ a = 1$
Suy ra $t = 3 \Rightarrow {x^2} - \sqrt 2 x - 3 = 0$ có 2 nghiệm phân biệt thỏa mãn điều kiện
Vậy phương trình đã cho có $2$ nghiệm.
Cho \(a,\,\,b,\,\,c\) là các số thực dương khác \(1\) thỏa mãn \(\log _a^2b + \log _b^2c = {\log _a}\dfrac{c}{b} - 2{\log _b}\dfrac{c}{b} - 3.\) Gọi \(M,{\rm{ }}m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của \(P = {\log _a}b - {\log _b}c.\) Giá trị của biểu thức \(S = m - 3M\) bằng
Ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,\log _a^2b + \log _b^2c = {\log _a}\dfrac{c}{b} - 2{\log _b}\dfrac{c}{b} - 3\\ \Leftrightarrow \log _a^2b + \log _b^2c = {\log _a}c - {\log _a}b - 2{\log _b}c - 1\\ \Leftrightarrow \log _a^2b + \log _b^2c = {\log _b}c.{\log _a}b - {\log _a}b - 2{\log _b}c - 1\,\,\left( * \right)\end{array}\)
Đặt \({\log _a}b = x \Rightarrow {\log _b}c = x - P\).
Phương trình (*) \( \Leftrightarrow {x^2} + {\left( {x - P} \right)^2} = \left( {x - P} \right)x - x - 2\left( {x - P} \right) - 1\)
\(\begin{array}{l} \Leftrightarrow 2{x^2} - 2Px + {P^2} = {x^2} - Px - 3x + 2P - 1\\ \Leftrightarrow {x^2} - \left( {P - 3} \right)x + {P^2} - 2P + 1 = 0\,\,\,\left( {**} \right)\end{array}\)
Ta có: \(\Delta = {\left( {P - 3} \right)^2} - 4\left( {{P^2} - 2P + 1} \right) = - 3{P^2} + 2P + 5\)
Phương trình (**) có nghiệm \( \Leftrightarrow \Delta \ge 0 \Leftrightarrow - 3{P^2} + 2P + 5 \ge 0 \Leftrightarrow - 1 \le P \le \dfrac{5}{3}\,\, \Rightarrow \left\{ \begin{array}{l}m = - 1\\M = \dfrac{5}{3}\end{array} \right.\).
Vậy \(S = m - 3M = - 1 - 3.\dfrac{5}{3} = - 6\).
Cho các số thực \(a,\,\,b,\,\,c\) thuộc khoảng \(\left( {1; + \infty } \right)\) và thỏa mãn \(\log _{\sqrt a }^2b + {\log _b}c.{\log _b}\left( {\dfrac{{{c^2}}}{b}} \right) + 9{\log _a}c = 4{\log _a}b\). Giá trị của biểu thức \({\log _a}b + {\log _b}{c^2}\) bằng:
Ta có:
\(\begin{array}{l}\,\,\,\,\,\,\log _{\sqrt a }^2b + {\log _b}c.{\log _b}\left( {\dfrac{{{c^2}}}{b}} \right) + 9{\log _a}c = 4{\log _a}b\\ \Leftrightarrow 4\log _a^2b + {\log _b}c.\left( {2{{\log }_b}c - 1} \right) + 9{\log _a}c = 4{\log _a}b\\ \Leftrightarrow 4\log _a^2b + 2\log _b^2c - {\log _b}c + 9{\log _a}b.{\log _b}c = 4{\log _a}b\,\,\left( * \right)\end{array}\)
Đặt \(x = {\log _a}b,\,\,y = {\log _b}c\) ta có: \(\left\{ \begin{array}{l}x = {\log _a}b > {\log _a}1 = 0\\y = {\log _b}c > {\log _b}1 = 0\end{array} \right.\,\,\left( {do\,\,a,b,c > 1} \right)\).
Khi đó phương trình (*) trở thành:
\(\begin{array}{l}\,\,\,\,\,\,4{x^2} + 2{y^2} - y + 9xy = 4x\\ \Leftrightarrow 4{x^2} + xy + 8xy + 2{y^2} - y - 4x = 0\\ \Leftrightarrow x\left( {4x + y} \right) + 2y\left( {4x + y} \right) - \left( {4x + y} \right) = 0\\ \Leftrightarrow \left( {4x + y} \right)\left( {x + 2y - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}4x + y = 0\\x + 2y - 1 = 0\end{array} \right.\end{array}\)
TH1: \(y = - 4x\) loại do \(x,\,\,y > 0\).
TH2: \(x + 2y - 1 = 0 \Leftrightarrow x + 2y = 1\), khi đó ta có: \({\log _a}b + {\log _b}{c^2} = x + 2y = 1\).
Biết \(a,\,\,b\) là các số thực sao cho \({x^3} + {y^3} = a{.10^{3z}} + b{.10^{2z}}\), đồng thời \(x,\,\,y,\,\,z\) là các số thực dương thỏa mãn \(\log \left( {x + y} \right) = z\) và \(\log \left( {{x^2} + {y^2}} \right) = z + 1\). Giá trị của \(\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}\) thuộc khoảng:
Theo bài ra ta có: \(\left\{ \begin{array}{l}\log \left( {x + y} \right) = z\\\log \left( {{x^2} + {y^2}} \right) = z + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + y = {10^z}\\{x^2} + {y^2} = {10.10^z}\end{array} \right. \Leftrightarrow {x^2} + {y^2} = 10\left( {x + y} \right)\).
Khi đó ta có:
\(\begin{array}{l}\,\,\,\,\,{x^3} + {y^3} = a{.10^{3z}} + b{.10^{2z}}\\ \Leftrightarrow \left( {x + y} \right)\left( {{x^2} + {y^2} - xy} \right) = a.{\left( {{{10}^z}} \right)^3} + b.{\left( {{{10}^z}} \right)^2}\\ \Leftrightarrow \left( {x + y} \right)\left( {{x^2} + {y^2} - xy} \right) = a.{\left( {x + y} \right)^3} + b.{\left( {x + y} \right)^2}\\ \Leftrightarrow {x^2} + {y^2} - xy = a{\left( {x + y} \right)^2} + b\left( {x + y} \right)\\ \Leftrightarrow {x^2} + {y^2} - xy = a\left( {{x^2} + 2xy + {y^2}} \right) + b.\dfrac{{{x^2} + {y^2}}}{{10}}\\ \Leftrightarrow {x^2} + {y^2} - xy = \left( {a + \dfrac{b}{{10}}} \right)\left( {{x^2} + {y^2}} \right) + 2a.xy\end{array}\)
Đồng nhất hệ số ta có \(\left\{ \begin{array}{l}1 = a + \dfrac{b}{{10}}\\ - 1 = 2a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \dfrac{1}{2}\\b = 15\end{array} \right.\).
Vậy \(\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}} = 4 + \dfrac{1}{{225}} = \dfrac{{901}}{{225}} \approx 4,004 \in \left( {4;5} \right)\).
Cho phương trình: \({4^{ - \left| {x - m} \right|}}.{\log _{\sqrt 2 }}\left( {{x^2} - 2x + 3} \right) + {2^{2x - {x^2}}}.{\log _{\dfrac{1}{2}}}\left( {2\left| {x - m} \right| + 2} \right) = 0\) với \(m\) là tham số. Tổng tất cả các giá trị của tham số \(m\) để phương trình đã cho có ba nghiệm phân biệt là:
Ta có:
\(\begin{array}{l}\,\,\,\,\,{4^{ - \left| {x - m} \right|}}.{\log _{\sqrt 2 }}\left( {{x^2} - 2x + 3} \right) + {2^{2x - {x^2}}}.{\log _{\dfrac{1}{2}}}\left( {2\left| {x - m} \right| + 2} \right) = 0\\ \Leftrightarrow {2^{ - 2\left| {x - m} \right|}}.2.{\log _2}\left( {{x^2} - 2x + 3} \right) - {2^{2x - {x^2}}}.{\log _2}\left( {2\left| {x - m} \right| + 2} \right) = 0\\ \Leftrightarrow {2^{ - 2\left| {x - m} \right| + 1}}.{\log _2}\left( {{x^2} - 2x + 3} \right) = {2^{2x - {x^2}}}.{\log _2}\left( {2\left| {x - m} \right| + 2} \right)\\ \Leftrightarrow {2^{{x^2} - 2x}}.lo{g_2}\left( {{x^2} - 2x + 3} \right) = {2^{2\left| {x - m} \right| - 1}}.{\log _2}\left( {2\left| {x - m} \right| + 2} \right)\\ \Leftrightarrow {2^{{x^2} - 2x + 2}}.lo{g_2}\left( {{x^2} - 2x + 3} \right) = {2^{2\left| {x - m} \right| + 2}}.{\log _2}\left( {2\left| {x - m} \right| + 2} \right)\end{array}\)
Xét hàm đặc trưng \(f\left( t \right) = {2^t}.{\log _2}t\,\,\left( {t \ge 2} \right)\) ta có
\(f'\left( t \right) = {2^t}.\ln 2.{\log _2}t + {2^t}.\dfrac{1}{{t\ln 2}} > 0\,\,\forall t \ge 2\), do đó hàm số đồng biến trên \(\left[ {2; + \infty } \right)\).
Lại có \(f\left( {{x^2} - 2x + 3} \right) = f\left( {2\left| {x - m} \right| + 2} \right)\)
\(\begin{array}{l} \Leftrightarrow {x^2} - 2x + 3 = 2\left| {x - m} \right| + 2\\ \Leftrightarrow {x^2} - 2x + 1 = 2\left| {x - m} \right|\\ \Leftrightarrow {\left( {x - 1} \right)^2} = 2\left| {x - m} \right|\,\,\left( * \right)\end{array}\)
Để phương trình ban đầu có 3 nghiệm phân biệt thì phương trình (*) phải có 3 nghiệm phân biệt.
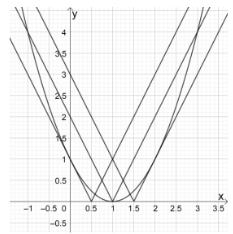
Dựa vào đồ thị hàm số ta có \(m = \dfrac{1}{2},\,\,m = 1,\,\,m = \dfrac{3}{2}\) thỏa mãn yêu cầu bài toán.
Cho các số thực dương \(a,\,\,b,\,\,c\) khác 1 thỏa mãn \(\log _a^2b + \log _b^2c + 2{\log _b}\dfrac{c}{b} = {\log _a}\dfrac{c}{{{a^3}b}}\). Gọi \(M,\,\,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P = {\log _a}ab - {\log _b}bc\). Tính giá trị của biểu thức \(S = 2{m^2} + 9{M^2}\).
Ta có:
\(\begin{array}{l}\,\,\,\,\,\,\log _a^2b + \log _b^2c + 2{\log _b}\dfrac{c}{b} = {\log _a}\dfrac{c}{{{a^3}b}}\\ \Leftrightarrow \log _a^2b + \log _b^2c + 2{\log _b}c - 2 = {\log _a}c - {\log _a}\left( {{a^3}b} \right)\\ \Leftrightarrow \log _a^2b + \log _b^2c + 2{\log _b}c - 2 = {\log _a}c - 3 - {\log _a}b\\ \Leftrightarrow \log _a^2b + \log _b^2c = {\log _a}b.lo{g_b}c - 2{\log _b}c - {\log _a}b - 1\,\,\,\left( 1 \right)\end{array}\)
Đặt \(x = {\log _a}b,\,\,y = {\log _b}c\), khi đó ta có:
\(\begin{array}{l}P = {\log _a}ab - {\log _b}bc\\P = 1 + {\log _a}b - 1 - {\log _b}c\\P = x - y \Rightarrow y = x - P\end{array}\)
Thay \(x,\,\,y\) vào (1) ta có:
\(\begin{array}{l}{x^2} + {y^2} = xy - 2y - x - 1\\ \Leftrightarrow {x^2} + {\left( {x - P} \right)^2} = x\left( {x - P} \right) - 2\left( {x - P} \right) - x - 1\\ \Leftrightarrow {x^2} + {x^2} - 2Px + {P^2} = {x^2} - Px - 2x + 2P - x - 1\\ \Leftrightarrow {x^2} - \left( {P - 3} \right)x + {P^2} - 2P + 1 = 0\,\,\left( 2 \right)\end{array}\)
Để tồn tại các số \(a,\,\,b,\,\,c\) thỏa mãn yêu cầu bài toán thì phương trình (2) phải có nghiệm.
\(\begin{array}{l} \Rightarrow \Delta \ge 0\\ \Leftrightarrow {\left( {P - 3} \right)^2} - 4\left( {{P^2} - 2P + 1} \right) \ge 0\\ \Leftrightarrow {P^2} - 6P + 9 - 4{P^2} + 8P - 4 \ge 0\\ \Leftrightarrow - 3{P^2} + 2P + 5 \ge 0\\ \Leftrightarrow - 1 \le P \le \dfrac{5}{3}\end{array}\)
Vậy \(m = - 1,\,\,M = \dfrac{5}{3}\) \( \Rightarrow S = 2{m^2} + 9{M^2} = 2.{\left( { - 1} \right)^2} + 9.{\left( {\dfrac{5}{3}} \right)^2} = 27\).
Số nghiệm của phương trình \({\log _3}\left| {{x^2} - x\sqrt 2 } \right| = {\log _5}\left( {{x^2} - x\sqrt 2 + 2} \right)\)
Bước 1:
Điều kiện: \(\left\{ \begin{array}{l}{x^2} - x\sqrt 2 + 2 > 0\\{x^2} - x\sqrt 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\x \ne \sqrt 2 \end{array} \right.\)
Đặt \({\log _3}\left| {{x^2} - x\sqrt 2 } \right| = {\log _5}\left( {{x^2} - x\sqrt 2 + 2} \right) = t\)
Ta có: \(\left| {{x^2} - x\sqrt 2 } \right| = {3^t},{x^2} - x\sqrt 2 + 2 = {5^t}\)
Bước 2: Xét các trường hợp ${x^2} - x\sqrt 2 >0$ và ${x^2} - x\sqrt 2 <0$
TH1: \({x^2} - x\sqrt 2 = {3^t}\)
Ta có \({3^t} + 2 = {5^t} \Leftrightarrow {\left( {\dfrac{3}{5}} \right)^t} + 2.{\left( {\dfrac{1}{5}} \right)^t} = 1\left( 1 \right)\)
Dễ thấy hàm số \(f\left( t \right) = {\left( {\dfrac{3}{5}} \right)^t} + 2{\left( {\dfrac{1}{5}} \right)^t}\) nghịch biến trên \(\mathbb{R}\).
Mà \(\left( 1 \right) \Leftrightarrow f\left( t \right) = f\left( 1 \right)\).
Vậy phương trình (1) nhận nghiệm \(t = 1\) là nghiệm duy nhất
Ta có
\(\begin{array}{l}{x^2} - x\sqrt 2 = {3^1} = 3 \Leftrightarrow {x^2} - x\sqrt 2 - 3 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{\sqrt 2 + \sqrt {14} }}{2}\left( {tm} \right)\\x = \dfrac{{\sqrt 2 - \sqrt {14} }}{2}\left( {tm} \right)\end{array} \right.\end{array}\)
TH2: \({x^2} - x\sqrt 2 = - {3^t}\)
Ta có \( - {3^t} + 2 = {5^t} \Leftrightarrow {5^t} + {3^t} = 2\left( 2 \right)\)
Ta thấy hàm số \(g\left( t \right) = {5^t} + {3^t}\) đồng biến trên \(\mathbb{R}\).
Mà \(\left( 2 \right) \Leftrightarrow g\left( t \right) = g\left( 0 \right)\)
Suy ra \(t = 0\)\( \Rightarrow {x^2} - x\sqrt 2 + 1 = 0\left( {VN} \right)\)
Vậy phương trình đã cho có hai nghiệm phân biệt.
Chu kì bán rã của nguyên tố phóng xạ Poloni 210 là 138 ngày (nghĩa là sau 138 ngày khối lượng của nguyên tố đó chỉ còn một nửa). Biết ban đầu có $m$ (gam) Poloni 210. Sau ít nhất bao nhiêu ngày thì khối lượng Poloni 210 còn lại bằng $\dfrac{1}{10}$ khối lượng ban đầu?
459 ngày
459 ngày
459 ngày
Bước 1: Biểu diễn lượng Poloni 210 theo m sau n ngày.
Lượng Poloni 210 ban đầu $T_{0}=m$. Lượg Poloni 210 còn lại sau 138 ngày: $T_{1}=\dfrac{1}{2} m$
Lượng Poloni 210 còn lại sau $138 \times 2$ ngày: $T_{2}=\left(\dfrac{1}{2}\right)^{2} m$
Cứ như vậy lượng Poloni 210 còn lại sau $138 \times n$ ngày: $T_{n}=\left(\dfrac{1}{2}\right)^{n} m$
Bước 2: Lập phương trình từ giả thiết và tìm n, từ đó biểu diễn lượng Poloni còn lại sau n ngày so với khối lượng ban đầu.
Yêu cầu bài toán tương đương $\left(\dfrac{1}{2}\right)^{n} m=\dfrac{1}{10} m \Leftrightarrow n=\log _{\dfrac{1}{2}} \dfrac{1}{10}$
Vậy sau ít nhất $138 \times n=138 \times \log _{\dfrac{1}{2}} \dfrac{1}{10} \approx 459$ ngày thì khối lượng Poloni 210 còn lại bằng $\dfrac{1}{10}$ khối lượng ban đầu.
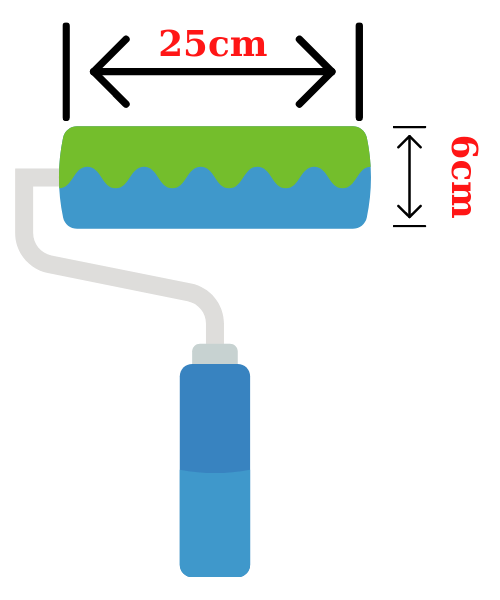
Một cái trục lăn sơn nước có dạng một hình trụ. Đường kính của đường tròn đáy là $6 \mathrm{~cm}$, chiều dài lăn là $25 \mathrm{~cm}$. Sau khi lăn trọn 10 vòng thì trục lăn tạo một diện tích trên bức tường phẳng bằng
$1500 \pi\left(\mathrm{cm}^{2}\right)$
$1500 \pi\left(\mathrm{cm}^{2}\right)$
$1500 \pi\left(\mathrm{cm}^{2}\right)$
Bước 1: Tính diện tích xung quanh của hình trụ
Diện tích xung quanh của hình trụ là $S_{xq}=2 \pi R h=\pi .6 .25=150 \pi\left(\mathrm{cm}^{2}\right) .$
Khi lăn sơn quay một vòng sẽ quét được một diện tích bằng diện tích xung quanh của hình trụ.
Bước 2: Tính diện tích sau khi trục lăn quay 10 vòng
Do đó trục lăn quay 10 vòng sẽ quét được diện tích là
$S=10 . S_{xq}=1500 \pi\left(\mathrm{cm}^{2}\right)$
Có bao nhiêu giá trị nguyên dương của tham số $m$ nhỏ hơn 2020 để phương trình $\log _{2}\left(m+\sqrt{m+2^{x}}\right)=2 x$ có nghiệm thực?
$2019$
$2019$
$2019$
Bước 1: Biến đổi phương trình, xét hàm đặc trưng $f(t)=t^{2}+t$
Phương trình đã cho tương đương với phương trình
\(\begin{array}{l}m + \sqrt {m + {2^x}} = {2^{2x}}\\ \Leftrightarrow \left( {m + {2^x}} \right) + \sqrt {m + {2^x}} = {2^{2x}} + {2^x}{\rm{ (1)}}\end{array}\)
Vì m nguyên dương nên $\sqrt{m+2^{x}} \geq \sqrt{2^{x}}>0$
Xét hàm đặc trưng $f(t)=t^{2}+t$ trên $[0 ;+\infty)$
Ta có $f^{\prime}(t)=2 t+1 \geq 0, \forall t \in[0 ;+\infty)$
$\Rightarrow f(t)$ đồng biến trên khoảng $[0 ;+\infty)$
Bước 2: Lập phương trình từ hàm đặc trưng. Tìm m.
Do đó $(1) \Leftrightarrow f\left(\sqrt{m+2^{x}}\right)=f\left(2^{x}\right) \Leftrightarrow \sqrt{m+2^{x}}=2^{x} \Leftrightarrow m=2^{2 x}-2^{x}(2)$
Đặt $a=2^{x}, a>0$. Ta có $(2) \Leftrightarrow m=g(a)=a^{2}-a$
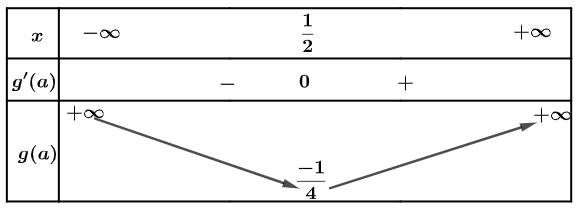
Phương trình đã cho có nghiệm $\Leftrightarrow$ đường thẳng $y=m$ cắt đồ thị hàm số $y=g(a)$ $\Leftrightarrow m \geq-\dfrac{1}{4}$ mà $m$ là giá trị nguyên dương nhỏ hơn 2020 nên $m \in\{1 ; 2 ; 3 ; \ldots ; 2019\}$
Vậy có 2019 giá trị $m$ thỏa mãn yêu cầu bài toán
Tích tất cả các nghiệm của phương trình \(2{\left( {{{\log }_4}x} \right)^2} - 3{\log _4}x - 2 = 0\)
TXĐ: \(D = \left( {0; + \infty } \right)\)
Đặt \(t = {\log _4}x\)
Phương trình đã cho trở thành:
\(\begin{array}{l}2{t^2} - 3t - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 2\\t = - \dfrac{1}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{\log _4}x = 2\\{\log _4}x = - \dfrac{1}{2}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 16\\x = \dfrac{1}{2}\end{array} \right.\end{array}\)
Tích các nghiệm là 8.

