Có bao nhiêu giá trị nguyên dương của tham số $m$ nhỏ hơn 2020 để phương trình $\log _{2}\left(m+\sqrt{m+2^{x}}\right)=2 x$ có nghiệm thực?
Trả lời bởi giáo viên
$2019$
Bước 1: Biến đổi phương trình, xét hàm đặc trưng $f(t)=t^{2}+t$
Phương trình đã cho tương đương với phương trình
\(\begin{array}{l}m + \sqrt {m + {2^x}} = {2^{2x}}\\ \Leftrightarrow \left( {m + {2^x}} \right) + \sqrt {m + {2^x}} = {2^{2x}} + {2^x}{\rm{ (1)}}\end{array}\)
Vì m nguyên dương nên $\sqrt{m+2^{x}} \geq \sqrt{2^{x}}>0$
Xét hàm đặc trưng $f(t)=t^{2}+t$ trên $[0 ;+\infty)$
Ta có $f^{\prime}(t)=2 t+1 \geq 0, \forall t \in[0 ;+\infty)$
$\Rightarrow f(t)$ đồng biến trên khoảng $[0 ;+\infty)$
Bước 2: Lập phương trình từ hàm đặc trưng. Tìm m.
Do đó $(1) \Leftrightarrow f\left(\sqrt{m+2^{x}}\right)=f\left(2^{x}\right) \Leftrightarrow \sqrt{m+2^{x}}=2^{x} \Leftrightarrow m=2^{2 x}-2^{x}(2)$
Đặt $a=2^{x}, a>0$. Ta có $(2) \Leftrightarrow m=g(a)=a^{2}-a$
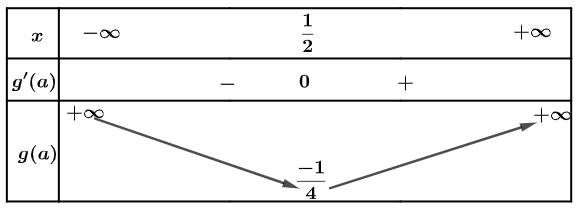
Phương trình đã cho có nghiệm $\Leftrightarrow$ đường thẳng $y=m$ cắt đồ thị hàm số $y=g(a)$ $\Leftrightarrow m \geq-\dfrac{1}{4}$ mà $m$ là giá trị nguyên dương nhỏ hơn 2020 nên $m \in\{1 ; 2 ; 3 ; \ldots ; 2019\}$
Vậy có 2019 giá trị $m$ thỏa mãn yêu cầu bài toán
Hướng dẫn giải:
Bước 1: Biến đổi phương trình, xét hàm đặc trưng $f(t)=t^{2}+t$
Bước 2: Lập phương trình từ hàm đặc trưng. Tìm m.

