Cho phương trình: \({4^{ - \left| {x - m} \right|}}.{\log _{\sqrt 2 }}\left( {{x^2} - 2x + 3} \right) + {2^{2x - {x^2}}}.{\log _{\dfrac{1}{2}}}\left( {2\left| {x - m} \right| + 2} \right) = 0\) với \(m\) là tham số. Tổng tất cả các giá trị của tham số \(m\) để phương trình đã cho có ba nghiệm phân biệt là:

Ta có:

\(\begin{array}{l}\,\,\,\,\,{4^{ - \left| {x - m} \right|}}.{\log _{\sqrt 2 }}\left( {{x^2} - 2x + 3} \right) + {2^{2x - {x^2}}}.{\log _{\dfrac{1}{2}}}\left( {2\left| {x - m} \right| + 2} \right) = 0\\ \Leftrightarrow {2^{ - 2\left| {x - m} \right|}}.2.{\log _2}\left( {{x^2} - 2x + 3} \right) - {2^{2x - {x^2}}}.{\log _2}\left( {2\left| {x - m} \right| + 2} \right) = 0\\ \Leftrightarrow {2^{ - 2\left| {x - m} \right| + 1}}.{\log _2}\left( {{x^2} - 2x + 3} \right) = {2^{2x - {x^2}}}.{\log _2}\left( {2\left| {x - m} \right| + 2} \right)\\ \Leftrightarrow {2^{{x^2} - 2x}}.lo{g_2}\left( {{x^2} - 2x + 3} \right) = {2^{2\left| {x - m} \right| - 1}}.{\log _2}\left( {2\left| {x - m} \right| + 2} \right)\\ \Leftrightarrow {2^{{x^2} - 2x + 2}}.lo{g_2}\left( {{x^2} - 2x + 3} \right) = {2^{2\left| {x - m} \right| + 2}}.{\log _2}\left( {2\left| {x - m} \right| + 2} \right)\end{array}\)

Xét hàm đặc trưng \(f\left( t \right) = {2^t}.{\log _2}t\,\,\left( {t \ge 2} \right)\) ta có

\(f'\left( t \right) = {2^t}.\ln 2.{\log _2}t + {2^t}.\dfrac{1}{{t\ln 2}} > 0\,\,\forall t \ge 2\), do đó hàm số đồng biến trên \(\left[ {2; + \infty } \right)\).

Lại có \(f\left( {{x^2} - 2x + 3} \right) = f\left( {2\left| {x - m} \right| + 2} \right)\)

\(\begin{array}{l} \Leftrightarrow {x^2} - 2x + 3 = 2\left| {x - m} \right| + 2\\ \Leftrightarrow {x^2} - 2x + 1 = 2\left| {x - m} \right|\\ \Leftrightarrow {\left( {x - 1} \right)^2} = 2\left| {x - m} \right|\,\,\left( * \right)\end{array}\)

Để phương trình ban đầu có 3 nghiệm phân biệt thì phương trình (*) phải có 3 nghiệm phân biệt.

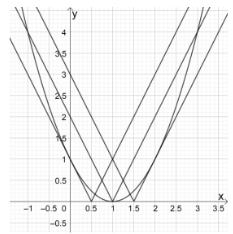
Dựa vào đồ thị hàm số ta có \(m = \dfrac{1}{2},\,\,m = 1,\,\,m = \dfrac{3}{2}\) thỏa mãn yêu cầu bài toán.