Bài tập cơ năng - Định luật bảo toàn cơ năng

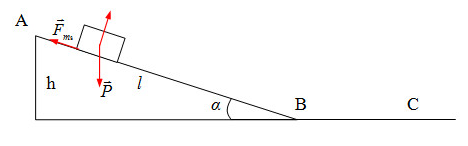
Ta có:

+ Cơ năng tại A: \({{\rm{W}}_A} = mgh = 1.9,8.1 = 9,8J\)

+ Trong khi vật chuyển động từ A đến B, tại B cơ năng chuyển hóa thành động năng tại B và công để thắng lực ma sát

Áp dụng định luật bảo toàn chuyển hóa năng lượng, ta có:

\({{\rm{W}}_A} = {{\rm{W}}_{{d_B}}} + {A_{{F_{ms}}}}\)  (1)

Chọn chiều dương trùng chiều chuyển động của vật

Ta có:

+ Động năng tại B: \({{\rm{W}}_{{d_B}}} = \dfrac{1}{2}mv_B^2\)

+ Công của lực ma sát: \(A = {F_{ms}}.s.cos\beta  =  - {F_{ms}}.l =  - \mu P.\sin \alpha .l\)

Thay vào (1) ta được:

\(\begin{array}{l}{{\rm{W}}_A} = {{\rm{W}}_{{d_B}}} + \left| {{A_{{F_{ms}}}}} \right|\\ \leftrightarrow 9,8 = \dfrac{1}{2}mv_B^2 + \left| { - \mu .P.\sin \alpha .l} \right|\\ \leftrightarrow 9,8 = \dfrac{1}{2}m.v_B^2 + \left| { - \mu mg.\dfrac{h}{l}.l} \right|\\ \leftrightarrow 9,8 = \dfrac{1}{2}1.v_B^2 + \left| { - 0,05.1.9,8.\dfrac{1}{{10}}.10} \right|\\ \to v_B^2 = 18,62\\ \to {v_B} \approx 4,32m/s\end{array}\)

Ta có:

+ Cơ năng tại A: \({{\rm{W}}_A} = mgh = 1.9,8.1 = 9,8J\)

+ Trong khi vật chuyển động từ A đến B, tại B cơ năng chuyển hóa thành động năng tại B và công để thắng lực ma sát

Áp dụng định luật bảo toàn chuyển hóa năng lượng, ta có:

\({{\rm{W}}_A} = {{\rm{W}}_{{d_B}}} + {A_{{F_{ms}}}}\)  (1)

Chọn chiều dương trùng chiều chuyển động của vật

Ta có:

+ Động năng tại B: \({{\rm{W}}_{{d_B}}} = \dfrac{1}{2}mv_B^2\)

+ Công của lực ma sát: \(A = {F_{ms}}.s.cos\beta  =  - {F_{ms}}.l =  - \mu P.\sin \alpha .l\)

Thay vào (1) ta được:

\(\begin{array}{l}{{\rm{W}}_A} = {{\rm{W}}_{{d_B}}} + \left| {{A_{{F_{ms}}}}} \right|\\ \leftrightarrow 9,8 = \dfrac{1}{2}mv_B^2 + \left| { - \mu .P.\sin \alpha .l} \right|\\ \leftrightarrow 9,8 = \dfrac{1}{2}m.v_B^2 + \left| { - \mu mg.\dfrac{h}{l}.l} \right|\\ \leftrightarrow 9,8 = \dfrac{1}{2}1.v_B^2 + \left| { - 0,05.1.9,8.\dfrac{1}{{10}}.10} \right|\\ \to v_B^2 = 18,62\\ \to {v_B} \approx 4,32m/s\end{array}\)

Các đại lượng động lượng, động năng và cơ năng đều phụ thuộc vào vận tốc nên khi chuyển động, vật đều có động lượng, động năng và cơ năng nhưng vật có thể không có thế năng do cách ta chọn gốc thế năng.

=> Phương án C - sai

Ta có, khi vật được thả rơi tự do, trong quá trình rơi thì động năng và thế năng của vật luôn thay đổi, cơ năng của vật không đổi

Cụ thể thế năng giảm và động năng tăng

Ta có, vận động viên trượt tuyết từ trên vách núi trượt xuống, tốc độ trượt mỗi lúc một tăng

=> Động năng của vận động viên tăng

Bên cạnh đó thế năng của vận động viên giảm do khoảng cách của vận động viên với chân núi giảm

A – đúng

B – sai vì: Tại VTCB thế năng của con lắc cực tiểu

C – sai vì: Cơ năng của con lắc được bảo toàn

D – sai vì: Tại VTCB động năng cực đại, thế năng cực tiểu và cơ năng bảo toàn

Cơ năng của một vật được xác định bằng tổng động năng và thế năng của vật đó

\({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t}\)

Ta có:

+ Thế năng: \({{\rm{W}}_t} = mgz\)

+ Động năng: \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\)

+ Cơ năng: \({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t}\)

+ Động lượng: \(\overrightarrow p  = m\overrightarrow v \)

Khi vật được ném ngang, ta có vận tốc và độ cao của vật so với đất luôn thay đổi

=> Động năng, thế năng, động lượng của vật luôn thay đổi

Cơ năng của vật không đổi vì cơ năng được bảo toàn

Từ định lí biến thiên động năng ta có:

\(\begin{array}{l}A = {W_{d2}} - {W_{d1}}\\ \Leftrightarrow {F_h}.s = 0 - \dfrac{1}{2}m{v^2}\\ \Rightarrow F{}_h =  - \dfrac{{m{v^2}}}{{2s}}\end{array}\)

Ta có : \(\left\{ \begin{array}{l}v = 18km/h = 5m/s\\m = 45kg\\s = 8m\end{array} \right.\)

\( \Rightarrow {F_h} =  - \dfrac{{{{45.5}^2}}}{{2.8}} \approx  - 70,3N\)

Độ lớn của lực hãm là: \( \Rightarrow {F_h} = 70,3N\)dấu ‘-‘ có nghĩa là lực cản trở chuyển động.

Chọn gốc thế năng tại vị trí ném

- Tại vị trí ném vật ta có:

+ Thế năng của vật tại đó: \({{\rm{W}}_t} = 0\)

+ Động năng của vật tại đó: \({{\rm{W}}_d} = \dfrac{1}{2}mv_0^2 = \dfrac{1}{2}.0,{02.5^2} = 0,25J\)

=> Cơ năng của vật: \({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t} = 0,25 + 0 = 0,25J\)

- Tại vị trí cao nhất, ta có:

+ Thế năng: \({{\rm{W}}_t} = mg{h_{max}}\)

+ Động năng: \({{\rm{W}}_d} = 0\)

=> Cơ năng của vật tại vị trí cao nhất: \({{\rm{W}}_{{h_{max}}}} = {{\rm{W}}_t} + {{\rm{W}}_d} = mg{h_{max}}\)

- Áp dụng định luật bảo toàn cơ năng cho 2 vị trí (lúc ném vật và khi vật đạt độ cao cực đại), ta có:

\(\dfrac{1}{2}mv_0^2 = mg{h_{max}} \to {h_{max}} = \dfrac{{v_0^2}}{{2g}} = \dfrac{{{5^2}}}{{2.10}} = 1,25m\)

Các đại lượng động lượng, động năng và cơ năng đều phụ thuộc vào vận tốc nên khi chuyển động, vật đều có động lượng, động năng và cơ năng nhưng vật có thể không có thế năng do cách ta chọn gốc thế năng.

Chọn gốc thế năng tại vị trí ném

Tại vị trí ném vật ta có:

+ Thế năng của vật tại đó: \({{\rm{W}}_t} = 0\)

+ Động năng của vật tại đó: \({{\rm{W}}_d} = \dfrac{1}{2}mv_0^2 = \dfrac{1}{2}.0,{02.5^2} = 0,25J\)

=> Cơ năng của vật: \({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t} = 0,25 + 0 = 0,25J\)

Chọn gốc thế năng tại vị trí ném

Tại vị trí ném vật ta có:

+ Thế năng của vật tại đó: \({{\rm{W}}_t} = 0\)

+ Động năng của vật tại đó: \({{\rm{W}}_d} = \dfrac{1}{2}mv_0^2 = \dfrac{1}{2}.0,{02.5^2} = 0,25J\)

=> Cơ năng của vật: \({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t} = 0,25 + 0 = 0,25J\)

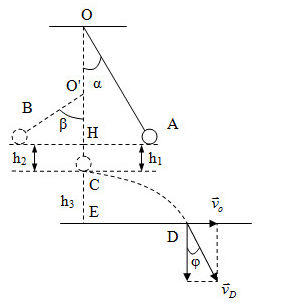
Chọn gốc thế năng tại vị trí cân bằng (C)

+ Áp dụng định luật bảo toàn cơ năng tại hai điểm A và B, ta có:

\({{\rm{W}}_A} = {{\rm{W}}_B} \leftrightarrow mg{h_1} = mg{h_2} \to {h_1} = {h_2}\)  (1)

Mặt khác, ta có: \({h_1} = l\left( {1 - cos\alpha } \right)\)

Thế vào (1) ta suy ra: \({h_1} = {h_2} = l\left( {1 - cos\alpha } \right) = 1,2\left( {1 - cos{{30}^0}} \right) = 0,1607m\)

Từ hình ta có:

\(\begin{array}{l}cos\beta  = \dfrac{{O'H}}{{O'B}} = \dfrac{{\dfrac{l}{2} - {h_1}}}{{\dfrac{l}{2}}} = \dfrac{{\dfrac{{1,2}}{2} - 0,1607}}{{\dfrac{{1,2}}{2}}} = 0,732\\ \to \beta  = 42,{9^0}\end{array}\)

+ Ta có cơ năng tại B: \({{\rm{W}}_B} = mg{h_2}\)

Cơ năng tại C: \({{\rm{W}}_C} = \dfrac{1}{2}mv_C^2\)

+ Áp dụng định luật bảo toàn cơ năng tại 2 vị trí B và C, ta có:

\({{\rm{W}}_B} = {{\rm{W}}_C} \leftrightarrow mg{h_2} = \dfrac{1}{2}mv_C^2 \to {v_C} = \sqrt {2g{h_2}}  = \sqrt {2.10.0,1607}  = 1,79m/s\)

+ Khi quay lại C, dây bị đứt chuyển động của vật coi như chuyển động ném ngang với vận tốc ban đầu \({v_0} = 1,79m/s\)

Áp dụng định luật bảo toàn cơ năng cho điểm C và D (chọn gốc thế năng tại mặt đất)

\({{\rm{W}}_C} = {{\rm{W}}_D} \leftrightarrow \dfrac{1}{2}mv_C^2 + mg{h_3} = \dfrac{1}{2}mv_D^2\)  (2)

Ta có: \(\left\{ \begin{array}{l}m = 100g = 0,1kg\\{v_C} = 1,79m/s\\{h_3} = 2 - l = 2 - 1,2 = 0,8m\end{array} \right.\)

Thế vào (2), ta được:

\(\begin{array}{l}\dfrac{1}{2}.0,1.1,{79^2} + 0,1.10.0,8 = \dfrac{1}{2}0,1.v_D^2\\ \to {v_D} = 4,38m/s\end{array}\)

Chọn gốc thế năng tại vị trí cân bằng (C)

+ Áp dụng định luật bảo toàn cơ năng tại hai điểm A và B, ta có:

\({{\rm{W}}_A} = {{\rm{W}}_B} \leftrightarrow mg{h_1} = mg{h_2} \to {h_1} = {h_2}\)  (1)

Mặt khác, ta có: \({h_1} = l\left( {1 - cos\alpha } \right)\)

Thế vào (1) ta suy ra: \({h_1} = {h_2} = l\left( {1 - cos\alpha } \right) = 1,2\left( {1 - cos{{30}^0}} \right) = 0,1607m\)

 Từ hình ta có:

\(\begin{array}{l}cos\beta  = \dfrac{{O'H}}{{O'B}} = \dfrac{{\dfrac{l}{2} - {h_1}}}{{\dfrac{l}{2}}} = \dfrac{{\dfrac{{1,2}}{2} - 0,1607}}{{\dfrac{{1,2}}{2}}} = 0,732\\ \to \beta  = 42,{9^0}\end{array}\)

Chọn gốc thế năng tại vị trí cân bằng (C)

+ Áp dụng định luật bảo toàn cơ năng tại hai điểm A và B, ta có:

\({{\rm{W}}_A} = {{\rm{W}}_B} \leftrightarrow mg{h_1} = mg{h_2} \to {h_1} = {h_2}\)  (1)

Mặt khác, ta có: \({h_1} = l\left( {1 - cos\alpha } \right)\)

Thế vào (1) ta suy ra: \({h_1} = {h_2} = l\left( {1 - cos\alpha } \right) = 1,2\left( {1 - cos{{30}^0}} \right) = 0,1607m\)

 Từ hình ta có:

\(\begin{array}{l}cos\beta  = \dfrac{{O'H}}{{O'B}} = \dfrac{{\dfrac{l}{2} - {h_1}}}{{\dfrac{l}{2}}} = \dfrac{{\dfrac{{1,2}}{2} - 0,1607}}{{\dfrac{{1,2}}{2}}} = 0,732\\ \to \beta  = 42,{9^0}\end{array}\)

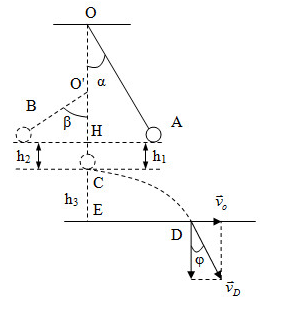
Chọn gốc thế năng tại mặt đất

Ta có,

+ Cơ năng của vật tại vị trí ném: \({\rm{W}} = mgh + \dfrac{1}{2}mv_0^2\)

+ Cơ năng của vật tại mặt đất: \({{\rm{W}}_{dat}} = \dfrac{1}{2}m{v^2}\)  (thế năng lúc này bằng 0)

Áp dụng định luật bảo toàn cơ năng cho 2 vị trí trên, ta được:

\(\begin{array}{l}{\rm{W}} = {{\rm{W}}_{dat}} \leftrightarrow mgh + \dfrac{1}{2}mv_0^2 = \dfrac{1}{2}m{v^2}\\ \leftrightarrow gh + \dfrac{1}{2}v_0^2 = \dfrac{1}{2}{v^2}\\ \leftrightarrow 10.2 + \dfrac{1}{2}{4^2} = \dfrac{1}{2}{v^2}\\ \to v \approx 7,5m/s\end{array}\)

Chọn mốc thế năng tại mặt đất, ta có:

+ Cơ năng tại vị  trí vật đạt độ cao cực đại = Thế năng cực đại vật đạt được: \({{\rm{W}}_{{t_{max}}}} = mg{h_{max}}\)

+ Cơ năng của vật khi chạm đất: \({{\rm{W}}_{cd}} = \dfrac{1}{2}m{v^2}\) (do thế năng lúc này bằng 0)

Áp dụng định luật bảo toàn cơ năng cho 2 vị trí trên, ta có:

\(\begin{array}{l}{{\rm{W}}_{{t_{max}}}} = {{\rm{W}}_{cd}} \leftrightarrow mg{h_{max}} = \dfrac{1}{2}m{v^2}\\ \to {h_{max}} = \dfrac{{{v^2}}}{{2g}} = \dfrac{{8,{4^2}}}{{2.10}} = 3,528m\end{array}\)

+ Cơ năng của vật tại vị trí ném: \({\rm{W}} = mgh + \dfrac{1}{2}mv_0^2\)

+ Cơ năng tại vị  trí vật đạt độ cao cực đại = Thế năng cực đại vật đạt được: \({{\rm{W}}_{{t_{max}}}} = mg{h_{max}}\)

Áp dụng định luật bảo toàn cơ năng cho 2 vị trí trên (vị trí ném và vị trí độ cao cực đại), ta được:

\(\begin{array}{l}mgh + \dfrac{1}{2}mv_0^2 = mg{h_{max}}\\ \leftrightarrow gh + \dfrac{1}{2}v_0^2 = g{h_{max}}\\ \leftrightarrow 10.2 + \dfrac{1}{2}v_0^2 = 10.3,528\\ \to {v_0} \approx 5,53m/s\end{array}\) 

Chọn mốc thế năng tại mặt đất, ta có:

+ Cơ năng tại vị  trí vật đạt độ cao cực đại = Thế năng cực đại vật đạt được: \({{\rm{W}}_{{t_{max}}}} = mg{h_{max}}\)

+ Cơ năng của vật khi chạm đất: \({{\rm{W}}_{cd}} = \dfrac{1}{2}m{v^2}\) (do thế năng lúc này bằng 0)

Áp dụng định luật bảo toàn cơ năng cho 2 vị trí trên, ta có:

\(\begin{array}{l}{{\rm{W}}_{{t_{max}}}} = {{\rm{W}}_{cd}} \leftrightarrow mg{h_{max}} = \dfrac{1}{2}m{v^2}\\ \to {h_{max}} = \dfrac{{{v^2}}}{{2g}} = \dfrac{{8,{4^2}}}{{2.10}} = 3,528m\end{array}\)

Chọn mốc thế năng tại mặt đất, ta có:

+ Cơ năng tại vị  trí vật đạt độ cao cực đại = Thế năng cực đại vật đạt được: \({{\rm{W}}_{{t_{max}}}} = mg{h_{max}}\)

+ Cơ năng của vật khi chạm đất: \({{\rm{W}}_{cd}} = \dfrac{1}{2}m{v^2}\) (do thế năng lúc này bằng 0)

Áp dụng định luật bảo toàn cơ năng cho 2 vị trí trên, ta có:

\(\begin{array}{l}{{\rm{W}}_{{t_{max}}}} = {{\rm{W}}_{cd}} \leftrightarrow mg{h_{max}} = \dfrac{1}{2}m{v^2}\\ \to {h_{max}} = \dfrac{{{v^2}}}{{2g}} = \dfrac{{8,{4^2}}}{{2.10}} = 3,528m\end{array}\)