Trả lời bởi giáo viên
Đáp án đúng: a
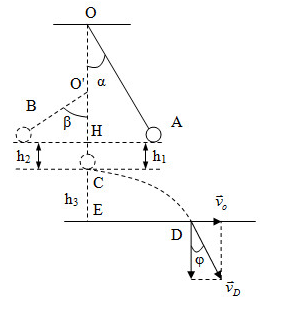
Chọn gốc thế năng tại vị trí cân bằng (C)
+ Áp dụng định luật bảo toàn cơ năng tại hai điểm A và B, ta có:
\({{\rm{W}}_A} = {{\rm{W}}_B} \leftrightarrow mg{h_1} = mg{h_2} \to {h_1} = {h_2}\) (1)
Mặt khác, ta có: \({h_1} = l\left( {1 - cos\alpha } \right)\)
Thế vào (1) ta suy ra: \({h_1} = {h_2} = l\left( {1 - cos\alpha } \right) = 1,2\left( {1 - cos{{30}^0}} \right) = 0,1607m\)
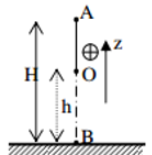
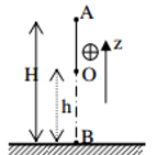
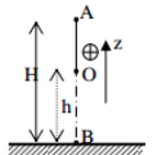
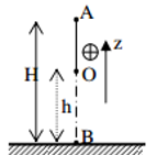
Từ hình ta có:
\(\begin{array}{l}cos\beta = \dfrac{{O'H}}{{O'B}} = \dfrac{{\dfrac{l}{2} - {h_1}}}{{\dfrac{l}{2}}} = \dfrac{{\dfrac{{1,2}}{2} - 0,1607}}{{\dfrac{{1,2}}{2}}} = 0,732\\ \to \beta = 42,{9^0}\end{array}\)
Hướng dẫn giải:
+ Áp dụng định luật bảo toàn cơ năng
+ Sử dụng điểu thức tính thế năng: \({{\rm{W}}_t} = mgh\)