Phương trình đường thẳng

Vì $d//Oz$ nên ta có \(\overrightarrow {{u_d}}  = \vec k = (0,0,1)\). Vì \(d\) qua $A\left( {1,2, - 3} \right)$ nên \(d\) có phương trình \(\left\{ \begin{array}{l}x = 1\\y = 2\\z =  - 3 + t\end{array} \right.\)(*)

Đối chiếu kết quả các đáp án ta thấy:

+ A,B, D sai vecto chỉ phương.

+ Đáp án C đúng vecto chỉ phương \(\overrightarrow {{u_d}} \). Kiểm tra điểm $B\left( {1,2,3} \right)$ thuộc (*) nên C đúng.

Ta có \(\overrightarrow {{u_{{d_1}}}}  = (2,1, - 1)\)  và  \(\overrightarrow {{u_{{d_2}}}}  = (3,2,2)\)

Vì $d$ vuông góc với \({d_1}\)  và \({d_2}\)  nên có \(\overrightarrow {{u_d}}  = \left[ {\overrightarrow {{u_{{d_1}}}} ,\overrightarrow {{u_{{d_2}}}} } \right] = \left( {4; - 7;1} \right)\)

Vì $d$ qua $A\left( {1,2,3} \right)$ nên có phương trình \(d:\dfrac{{x - 1}}{4} = \dfrac{{y - 2}}{{ - 7}} = \dfrac{{z - 3}}{1}\)

\(H\)  là trực tâm của $\Delta ABC \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {AH} .\overrightarrow {BC}  = 0\\\overrightarrow {BH} .\overrightarrow {AC}  = 0\\\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AH}  = 0\end{array} \right.$

Ta giả sử $H\left( {x,y,z} \right)$, ta có

\(\overrightarrow {BC}  = (0, - 3, - 4)\)

\(\overrightarrow {AC}  = ( - 2,0, - 4)\)

\(\overrightarrow {AH}  = (x - 2,y,z)\)

\(\overrightarrow {BH}  = (x,y - 3,z)\)

\(\overrightarrow {AB}  = ( - 2,3,0)\).

Điều kiện \(\overrightarrow {AH} .\overrightarrow {BC}  = 0 \Leftrightarrow 3y + 4z = 0\)

Điều kiện \(\overrightarrow {BH} .\overrightarrow {AC}  = 0 \Leftrightarrow x + 2z = 0\)

Ta tính \([\overrightarrow {AB} ,\overrightarrow {AC} ] = ( - 12, - 8,6)\).

Điều kiện \([\overrightarrow {AB} ,\overrightarrow {AC} ].\overrightarrow {AH}  = 0 \Leftrightarrow  - 12(x - 2) - 8y + 6z = 0 \Leftrightarrow  - 6x - 4y + 3z + 12 = 0\)

Giải hệ \(\left\{ {\begin{array}{*{20}{l}}{3y + 4z = 0}&{}\\{x + 2z = 0}&{}\\{ - 6x - 4y + 3z + 12 = 0}&{}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = \dfrac{{72}}{{61}}}&{}\\{y = \dfrac{{48}}{{61}}}&{}\\{z = \dfrac{{ - 36}}{{61}}}&{}\end{array}} \right.\)

Suy ra \(H(\dfrac{{72}}{{61}},\dfrac{{48}}{{61}},\dfrac{{ - 36}}{{61}})\)

Suy ra \(\overrightarrow {OH}  = (\dfrac{{72}}{{61}},\dfrac{{48}}{{61}},\dfrac{{ - 36}}{{61}})\)  là vecto chỉ phương của $OH$.

Chọn \(\vec u = (6,4, - 3)\)  là vecto chỉ phương của $OH$ và $OH$ qua $O\left( {0,0,0} \right)$ nên phương trình tham số là \(\left\{ {\begin{array}{*{20}{l}}{x = 6t}&{}\\{y = 4t}&{}\\{z =  - 3t}&{}\end{array}} \right.\)

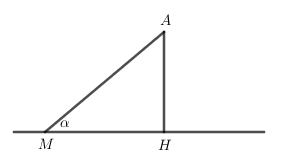
Đường thẳng \(\Delta \) đi qua điểm \(M\left( {2;5;7 - 2\sqrt 2 } \right)\) và nhận \(\overrightarrow u  = \left( {{m^2} - 2m;4 - m;0} \right)\) làm VTCP.

Có \(\overrightarrow {AM}  = \left( {1;3;4 - 2\sqrt 2 } \right) \Rightarrow AM= \sqrt{34 - 16\sqrt 2} \).

Để \(d\left( {A,\Delta } \right) = A{H_{\min }}\) thì \(\sin \alpha  = \dfrac{{AH}}{{AM}}\) đạt GTNN hay \(\cos \alpha \) đạt GTLN.

Mà \(\cos \alpha  = \cos \left( {AM,\Delta } \right) = \dfrac{{\left| {\overrightarrow {AM} .\overrightarrow u } \right|}}{{\left| {\overrightarrow {AM} } \right|.\left| {\overrightarrow u } \right|}} = \dfrac{{\left| {\left( {{m^2} - 2m} \right) + 3\left( {4 - m} \right)} \right|}}{{ {\sqrt{34 - 16\sqrt 2} }.\sqrt {{{\left( {{m^2} - 2m} \right)}^2} + {{\left( {4 - m} \right)}^2}} }}\) 

Mà \(\left| {\left( {{m^2} - 2m} \right) + 3\left( {4 - m} \right)} \right| \le \sqrt {{1^2} + {3^2}} .\sqrt {{{\left( {{m^2} - 2m} \right)}^2} + {{\left( {4 - m} \right)}^2}} \)

\( \Rightarrow \dfrac{{\left| {\left( {{m^2} - 2m} \right) + 3\left( {4 - m} \right)} \right|}}{{ {\sqrt{34 - 16\sqrt 2} }.\sqrt {{{\left( {{m^2} - 2m} \right)}^2} + {{\left( {4 - m} \right)}^2}} }} \le \dfrac{{\sqrt {10} }}{{\sqrt{34 - 16\sqrt 2} }}\) 

\( \Rightarrow \cos \alpha \) đạt GTLN nếu \(\dfrac{{{m^2} - 2m}}{1} = \dfrac{{4 - m}}{3} \Leftrightarrow 3{m^2} - 6m = 4 - m \Leftrightarrow 3{m^2} - 5m - 4 = 0\)

Phương trình này có hai nghiệm phân biệt do \(ac < 0\) nên tổng các giá trị của \(m\) là \(\dfrac{5}{3}\) .

- Thay tọa độ điểm \(A\left( {3 + m;\,\,4 + m;\,\,5 - 2m} \right)\) vào phương trình đường thẳng \(d\) ta có:

\(\dfrac{{3 + m - 3}}{1} = \dfrac{{4 + m - 4}}{1} = \dfrac{{5 - 2m - 5}}{{ - 2}} \Leftrightarrow m = m = m\) (luôn đúng) \( \Rightarrow A \in d\).

- Thay tọa độ điểm \(B\left( {4 - n;\,\,5 - n;\,\,3 + 2n} \right)\) vào phương trình đường thẳng \(d\) ta có:

\(\dfrac{{4 - n - 3}}{1} = \dfrac{{5 - n - 4}}{1} = \dfrac{{3 + 2n - 5}}{{ - 2}} \Leftrightarrow 1 - n = 1 - n = 1 - n\) (luôn đúng) \( \Rightarrow B \in d\).

Vậy \(A \in d,\,\,B \in d\).

Bước 1: Tìm vecto chỉ phương và tham số hóa hình chiếu M của A lên d.

Ta có:

\(d:\left\{ \begin{array}{l}x =  - 1 + t\\y =  - 3 + 2t\\z =  - 2 + 2t\end{array} \right.;\overrightarrow {{u_d}}  = \left( {1;\;2;\;2} \right)\)

Gọi \(M\) là hình chiếu vuông góc của \(A\) trên \(d\) và \({A}'\) đối xứng \(A\) qua \(d.\)

Suy ra \(M\left( m-1;2m-3;2m-2 \right)\) 

Bước 2: Biểu diễn \(\overrightarrow{AM}\) theo tham số và tìm điểm A'.

\(\overrightarrow{AM}=\left( m-4;2m-5;2m-2 \right)\)

Khi đó \(\overrightarrow{AM}.{{\vec{u}}_{d}}=0\Rightarrow \left( m-4 \right)+2\left( 2m-5 \right)+2\left( 2m-2 \right)=0\Leftrightarrow 9m=18\Leftrightarrow m=2.\)

Vậy \(M\left( 1;1;2 \right)\) và \(M\) là trung điểm \(A{A}'\) nên \({A}'\left( -1;0;4 \right).\)

Vậy $a+b+c=3$

Bước 1: Tìm giao điểm của \(d\) và \(\Delta \) và vectơ chỉ phương của đường thẳng \(d\)

Ta có điểm \(A(1; - 3;5)\) thuộc đường thẳng \(d\), nên \(A(1; - 3;5)\) là giao điểm của \(d\) và \(\Delta \). Một vectơ chỉ phương của đường thẳng \(d\) là \(\vec v( - 3;0; - 4)\).

Bước 2: Xét \(\overrightarrow {{u_1}}  = \dfrac{1}{{|\vec u|}} \cdot \vec u\) và \(\overrightarrow {{v_1}}  = \dfrac{1}{{|\vec v|}} \cdot \vec v\)

Ta xét \(\overrightarrow {{u_1}}  = \dfrac{1}{{|\vec u|}} \cdot \vec u = \dfrac{1}{3}(1;2; - 2)\)\( = \left( {\dfrac{1}{3};\dfrac{2}{3}; - \dfrac{2}{3}} \right);\)\(\overrightarrow {{v_1}}  = \dfrac{1}{{|\vec v|}} \cdot \vec v = \dfrac{1}{5}( - 3;0; - 4)\)\( = \left( { - \dfrac{3}{5};0; - \dfrac{4}{5}} \right)\).

Nhận thấy \(\overrightarrow {{u_1}}  \cdot \overrightarrow {{v_1}}  > 0\), nên góc tạo bởi hai vectơ \(\overrightarrow {{u_1}} ,\overrightarrow {{v_1}} \) là góc nhọn tạo bởi \(d\) và \(\Delta \).

Bước 3: \(\vec w = \overrightarrow {{u_1}}  + \overrightarrow {{v_1}} \)là vectơ chỉ phương của đường phân giác của góc nhọn tạo bởi \(d\) và \(\Delta \). Tìm phân giác.

Ta có \(\vec w = \overrightarrow {{u_1}}  + \overrightarrow {{v_1}}  = \left( { - \dfrac{4}{{15}};\dfrac{{10}}{{15}}; - \dfrac{{22}}{{15}}} \right)\)\( =  - \dfrac{2}{{15}}(2; - 5;11)\) là vectơ chỉ phương của đường phân giác của góc nhọn tạo bởi \(d\) và \(\Delta \) hay đường phân giác của góc nhọn tạo bởi \(d\)

Do đó, phương trình phân giác cần tìm là \(\left\{ {\begin{array}{*{20}{l}}{x = 1 + 2t}\\{y =  - 3 - 5t}\\{z = 5 + 11t}\end{array}} \right.\)

Thay t=t’-1 thì được phương trình \(\left\{ {\begin{array}{*{20}{l}}{x =  - 1 + 2t'}\\{y = 2 - 5t'}\\{z =  - 6 + 11t'}\end{array}} \right.\)

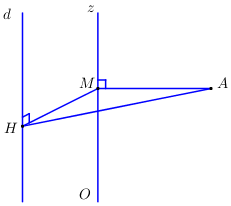
Gọi \({d_1}\) là khoảng cách từ \(A\) đến \(Oz\), \({d_2}\) là khoảng cách giữa \(Oz\) và \(d\).

Gọi \(M\) là hình chiếu của \(A\) trên \(Oz \Rightarrow M\left( {0;0; - 2} \right)\), ta có \(MA = 3 \Rightarrow d\left( {A;Oz} \right) = 3\).

Gọi \(H\) là hình chiếu của \(M\) trên \(d\) ta có \(HM \bot d\) và \(HM = 2\).

\(\left\{ \begin{array}{l}AM \bot Oz \Rightarrow AM \bot d\\HM \bot d\end{array} \right. \Rightarrow d \bot \left( {AMH} \right)\)\( \Rightarrow AH \bot d \Rightarrow d\left( {A;d} \right) = AH\).

Áp dụng định lí Cosin trong tam giác \(AHM\) ta có:

\(\begin{array}{l}\,\,\,\,\,\,A{H^2} = A{M^2} + H{M^2} - 2AM.HM.\cos \angle AMH\\ \Rightarrow A{H^2} = {3^2} + {2^2} - 2.3.2.\cos \angle AMH\\ \Rightarrow A{H^2} = 13 - 12\cos \angle AMH\end{array}\)

\( \Rightarrow A{H_{\max }} \Leftrightarrow A{H^2}_{\max } \Leftrightarrow \cos \angle AM{H_{\min }}\)

\( \Leftrightarrow \cos \angle AMH =  - 1 \Leftrightarrow \angle AMH = {180^0}\) hay \(A,\,\,M,\,\,H\) thằng hàng và \(M\) nằm giữa \(A\) và \(H\).

Khi đó ta có \(\dfrac{{AM}}{{HM}} = \dfrac{3}{2} \Rightarrow \overrightarrow {AM}  = \dfrac{3}{2}\overrightarrow {MH} \).

\( \Rightarrow \left( {0; - 3;0} \right) = \dfrac{3}{2}\left( {{x_H};{y_H};{z_H} - 2} \right)\)\( \Leftrightarrow \left\{ \begin{array}{l}\dfrac{3}{2}{x_H} = 0\\\dfrac{3}{2}{y_H} =  - 3\\\dfrac{3}{2}{z_H} - 3 = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_H} = 0\\{y_H} =  - 2\\{z_H} = 2\end{array} \right. \Rightarrow H\left( {0; - 2;2} \right)\)

\( \Rightarrow \) Phương trình đường thẳng \(d:\,\,\left\{ \begin{array}{l}x = 0\\y =  - 2\\z = 2 + t\end{array} \right.\).

Dựa vào các đáp án ta thấy chỉ có điểm \(P\left( {0; - 2; - 5} \right) \in d\).

\(M\) thay đổi trên đường thẳng \(d\,\, \Rightarrow M\left( {1 + 2t;1 + 2t; - 1 + t} \right)\).

Khi đó, \(P = MA + MB \)\(= \sqrt {{{\left( {2t - 5} \right)}^2} + {{\left( {2t + 1} \right)}^2} + {{\left( {t - 1} \right)}^2}}  \)\(+ \sqrt {{{\left( {2t + 1} \right)}^2} + {{\left( {2t + 1} \right)}^2} + {{\left( {t + 5} \right)}^2}} \)

\( = \sqrt {9{t^2} - 18t + 27}  + \sqrt {9{t^2} + 18t + 27} \)\( = 3\left[ {\sqrt {{{\left( {1 - t} \right)}^2} + {{\left( {\sqrt 2 } \right)}^2}}  + \sqrt {{{\left( {t + 1} \right)}^2} + {{\left( {\sqrt 2 } \right)}^2}} } \right]\)\( \ge 3\sqrt {{{\left( {1 - t + t + 1} \right)}^2} + {{\left( {\sqrt 2  + \sqrt 2 } \right)}^2}}  = 6\sqrt 3\)

Dấu “=” xảy ra khi và chỉ khi \(\dfrac{{1 - t}}{{\sqrt 2 }} = \dfrac{{t + 1}}{{\sqrt 2 }} \Leftrightarrow 1 - t = t + 1 \Leftrightarrow t = 0\).

Vậy \(\min P = 6\sqrt 3 \) khi và chỉ khi \(t = 0 \Leftrightarrow M\left( {1;1; - 1} \right)\).