Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ:{x=2+(m2−2m)ty=5−(m−4)tz=7−2√2 và điểm A(1;2;3). Gọi S là tập các giá trị thực của tham số m để khoảng cách từ A đến đường thẳng Δ có giá trị nhỏ nhất. Tổng các phần tử của S là
Trả lời bởi giáo viên
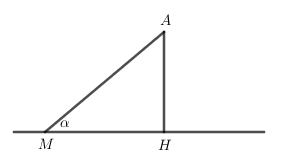
Đường thẳng Δ đi qua điểm M(2;5;7−2√2) và nhận →u=(m2−2m;4−m;0) làm VTCP.
Có →AM=(1;3;4−2√2)⇒AM=√34−16√2.
Để d(A,Δ)=AHmin thì \sin \alpha = \dfrac{{AH}}{{AM}} đạt GTNN hay \cos \alpha đạt GTLN.
Mà \cos \alpha = \cos \left( {AM,\Delta } \right) = \dfrac{{\left| {\overrightarrow {AM} .\overrightarrow u } \right|}}{{\left| {\overrightarrow {AM} } \right|.\left| {\overrightarrow u } \right|}} = \dfrac{{\left| {\left( {{m^2} - 2m} \right) + 3\left( {4 - m} \right)} \right|}}{{ {\sqrt{34 - 16\sqrt 2} }.\sqrt {{{\left( {{m^2} - 2m} \right)}^2} + {{\left( {4 - m} \right)}^2}} }}
Mà \left| {\left( {{m^2} - 2m} \right) + 3\left( {4 - m} \right)} \right| \le \sqrt {{1^2} + {3^2}} .\sqrt {{{\left( {{m^2} - 2m} \right)}^2} + {{\left( {4 - m} \right)}^2}}
\Rightarrow \dfrac{{\left| {\left( {{m^2} - 2m} \right) + 3\left( {4 - m} \right)} \right|}}{{ {\sqrt{34 - 16\sqrt 2} }.\sqrt {{{\left( {{m^2} - 2m} \right)}^2} + {{\left( {4 - m} \right)}^2}} }} \le \dfrac{{\sqrt {10} }}{{\sqrt{34 - 16\sqrt 2} }}
\Rightarrow \cos \alpha đạt GTLN nếu \dfrac{{{m^2} - 2m}}{1} = \dfrac{{4 - m}}{3} \Leftrightarrow 3{m^2} - 6m = 4 - m \Leftrightarrow 3{m^2} - 5m - 4 = 0
Phương trình này có hai nghiệm phân biệt do ac < 0 nên tổng các giá trị của m là \dfrac{5}{3} .
Hướng dẫn giải:
Khoảng cách từ điểm A đến đường thẳng \Delta là nhỏ nhất nếu góc tạo bởi đường thẳng AM với \Delta đạt GTNN.
Ở đó, M là điểm đi qua của \Delta .
Công thức tính góc giữa hai đường thẳng: \cos \alpha = \dfrac{{\left| {\overrightarrow {AM} .\overrightarrow u } \right|}}{{\left| {\overrightarrow {AM} } \right|.\left| {\overrightarrow u } \right|}} .

