Đề thi THPT QG - 2021 - mã 101
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
Hàm số đạt cực tiểu tại \(x = - 1\), giá trị cực tiểu bằng \( - 3\).
Đề thi THPT QG - 2021 - mã 102
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng
Ta có tại \(x = - 1\) hàm số đạt cực đại và giá trị \(f\left( x \right) = 3\).
Cho hàm số \(y = f(x)\) có đồ thị hàm số \(y = {f^\prime }(x)\) như hình bên dưới. Tìm số điểm cực trị của hàm số \(g(x) = f\left( {{x^2} - 3} \right)\).
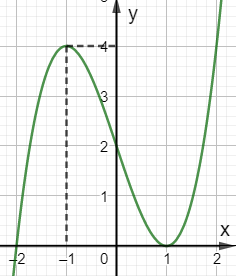
Bước 1: Tìm nghiệm của phương trình y’=0
Từ đồ thị hàm số ta có \(f'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 2}\\{x = 1}\end{array}} \right.\).
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{{x^2} - 3 = - 2}\\{{x^2} - 3 = 1{\text{ (nghiệm kép) }}}\end{array}} \right.\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = \pm 1}\\{x = \pm 2{\text{ (nghiệm kép) }}}\end{array}} \right.\)
Bước 2: Lập bảng biến thiên và tìm số cực trị
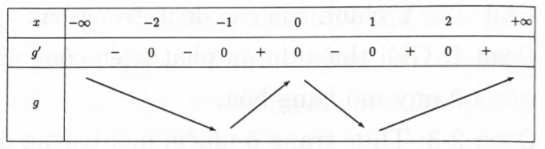
Dựa vào bảng biến thiên ta thấy hàm số có 3 điểm cực trị.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
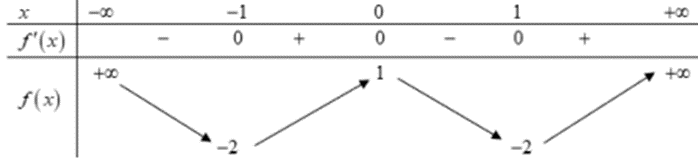
Số điểm cực trị của hàm số đã cho là:
$f'(x)$ đổi dấu tại \(x = - 1,\,\,x = 0,\,\,x = 1\) nên hàm số đã cho có 3 điểm cực trị \(x = - 1,\,\,x = 0,\,\,x = 1\).
Hàm số \(y = {\left( {{x^3} - 3x} \right)^e}\) có bao nhiêu điểm cực trị?
Điều kiện: \({x^3} - 3x > 0 \Leftrightarrow x\left( {{x^2} - 3} \right) > 0 \Leftrightarrow x\left( {x - \sqrt 3 } \right)\left( {x + \sqrt 3 } \right) > 0 \Leftrightarrow \left[ \begin{array}{l} - \sqrt 3 < x < 0\\x > \sqrt 3 \end{array} \right..\)
Ta có: \(y' = e\left( {3{x^2} - 3} \right){\left( {{x^3} - 3x} \right)^{e - 1}}.\)
\( \Rightarrow y' = 0 \Leftrightarrow \left( {3{x^2} - 3} \right){\left( {{x^3} - 3x} \right)^{e - 1}} = 0 \Leftrightarrow 3{x^2} - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\end{array} \right.\)
Ta có bảng xét dấu:
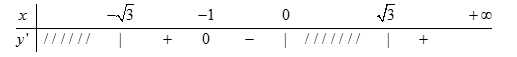
Dựa vào bảng xét dấu của hàm số ta thấy đạo hàm của hàm số chỉ đổi dấu qua 1 điểm \(x = - 1 \Rightarrow \) hàm số có 1 điểm cực trị.
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {{x^2} + x} \right){\left( {x - 2} \right)^2}\left( {{2^x} - 4} \right),\,\,\,\forall x \in \mathbb{R}.\) Số điểm cực trị của \(f\left( x \right)\) là:
Ta có: \(f'\left( x \right) = 0\)
\(\begin{array}{l} \Leftrightarrow \left( {{x^2} + x} \right){\left( {x - 2} \right)^2}\left( {{2^x} - 4} \right) = 0\\ \Leftrightarrow x\left( {x + 1} \right){\left( {x - 2} \right)^2}\left( {{2^x} - {2^2}} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x + 1 = 0\\x - 2 = 0\\{2^x} - {2^2} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 1\\x = 2\\x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\,\,\,\left( {bội\,\,1} \right)\\x = - 1\,\,\,\,\,\left( {bội\,\,1} \right)\\x = 2\,\,\,\,\,\left( {bội\,\,\,3} \right)\end{array} \right..\end{array}\)
Ta thầy phương trình \(f'\left( x \right) = 0\) có 3 nghiệm phân biệt và các nghiệm này đều là nghiệm bội lẻ nên hàm số \(y = f\left( x \right)\) có 3 điểm cực trị.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên sau
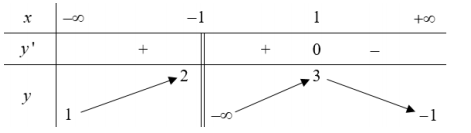
Khẳng định nào sau đây sai?
Từ BBT ta thấy hàm số đồng biến trên \(\left( { - \infty ; - 1} \right);\left( { - 1;1} \right)\) nên B sai vì trên khoảng \(\left( { - \infty ;1} \right)\) thì hàm số gián đoạn tại \(x = - 1.\)
Hàm số nghịch biến trên \(\left( {1; + \infty } \right)\) nên C đúng. Dễ thấy A đúng.
Lại có \(\mathop {\lim }\limits_{x \to - {1^ + }} x = - \infty \) nên \(x = - 1\) là TCĐ của đồ thị hàm số
Và \(\mathop {\lim }\limits_{x \to - \infty } y = 1;\,\mathop {\lim }\limits_{x \to + \infty } y = - 1\) nên \(y = 1;y = - 1\) là hai tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị hàm số có ba tiệm cận nên D đúng.
Tìm số điểm cực trị của hàm số \(y = \sin x - {\cos ^2}x\) trên \(\left[ {0;2\pi } \right]\)
TXĐ : \(D = \mathbb{R}\)
Ta có \(y = \sin x - {\cos ^2}x\)
$y' = \left( {\sin x - {{\cos }^2}x} \right)' $ $= \left( {\sin x} \right)' - \left( {{{\cos }^2}x} \right)' $ $= \cos x - 2\cos x\left( {\cos x} \right)' $ $= \cos x - 2\cos x\left( { - \sin x} \right) $ $= \cos x + 2\sin x\cos x$
Suy ra \(y' = 0 \) $ \Leftrightarrow \cos x\left( {1 + 2\sin x} \right) = 0$ \(\Leftrightarrow \left[ \begin{array}{l}\cos x = 0\\\sin x = - \dfrac{1}{2}\end{array} \right. \) \(\Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{2} + k\pi \\x = - \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{7\pi }}{6} + k2\pi \end{array} \right.\)
Mà \(x \in \left[ {0;2\pi } \right] \Rightarrow x = \dfrac{\pi }{2};x = \dfrac{{3\pi }}{2};x = \dfrac{{7\pi }}{6};x = \dfrac{{11\pi }}{6}\)
Có \(y' = \cos x + \sin 2x \Rightarrow y'' = - \sin x + 2\cos 2x\).
\(y''\left( {\dfrac{\pi }{2}} \right) = - 1 + 2\cos \pi = - 3 < 0\) nên \(x = \dfrac{\pi }{2}\) là điểm CĐ.
\(y''\left( {\dfrac{{3\pi }}{2}} \right) = - \sin \dfrac{{3\pi }}{2} + 2\cos 3\pi = 1 - 2 = - 1 < 0\) nên \(x = \dfrac{{3\pi }}{2}\) là điểm CĐ.
\(y''\left( {\dfrac{{7\pi }}{6}} \right) = - \sin \dfrac{{7\pi }}{6} + 2\cos \dfrac{{7\pi }}{3} = \dfrac{1}{2} + 1 = \dfrac{3}{2} > 0\) nên \(x = \dfrac{{7\pi }}{6}\) là điểm CT.
\(y''\left( {\dfrac{{11\pi }}{6}} \right) = - \sin \dfrac{{11\pi }}{6} + 2\cos \dfrac{{11\pi }}{3} = \dfrac{1}{2} + 1 = \dfrac{3}{2} > 0\) nên \(x = \dfrac{{11\pi }}{6}\) là điểm CT.
Vậy hàm số đã cho có \(4\) điểm cực trị.
Đề thi THPT QG - 2021 - mã 102
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
Ta có: \(f'\left( x \right)\) đổi dấu \(4\) lần nên hàm số có \(4\) điểm cực trị.
Hàm số \(y = {x^3} - 12x + 3\) đạt cực đại tại điểm
TXĐ: \(D = \mathbb{R}\).
Ta có: \(y' = 3{x^2} - 12,\,\,\,\,y'' = 6x\).
Xét hệ \(\left\{ \begin{array}{l}y' = 0\\y'' < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3{x^2} - 12 = 0\\6x < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \pm 2\\x < 0\end{array} \right. \Leftrightarrow x = - 2\).
Vậy hàm số đạt cực đại tại điểm \(x = - 2.\)
Cho hàm số \(y = f\left( x \right)\) liên tục tại \({x_0}\) và có bảng biến thiên sau
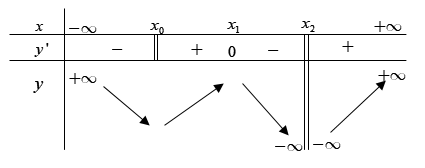
Mệnh đề nào sau đây là đúng ?
Hàm số có một điểm cực đại là \({x_1}\), một điểm cực tiểu là \({x_0}\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị \(f'\left( x \right)\) như hình vẽ bên. Số điểm cực đại của hàm số \(g\left( x \right) = f\left( { - {x^2} + x} \right)\) là:
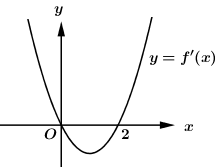
Ta có:
\(\begin{array}{l}g\left( x \right) = f\left( { - {x^2} + x} \right)\\ \Rightarrow g'\left( x \right) = \left( { - 2x + 1} \right)f'\left( { - {x^2} + x} \right)\\g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{1}{2}\\f'\left( { - {x^2} + x} \right) = 0\end{array} \right.\end{array}\)
Dựa vào đồ thị hàm số \(y = f'\left( x \right)\) ta có \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\).
\( \Rightarrow f'\left( { - {x^2} + x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} - {x^2} + x = 0\\ - {x^2} + x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\).
Suy ra phương trình \(g'\left( x \right) = 0\) có 3 nghiệm đơn phân biệt \(x = \dfrac{1}{2},\,\,x = 0,\,\,x = 1\).
Chọn \(x = 2\) ta có \(g'\left( 2 \right) = - 3f'\left( { - 2} \right) < 0\), qua các nghiệm \(x = \dfrac{1}{2},\,\,x = 0,\,\,x = 1\) thì \(g'\left( x \right)\) đổi dấu.
BBT:
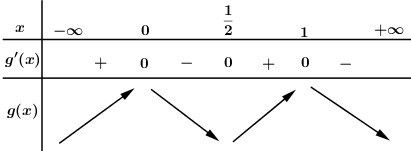
Dựa vào BBT ta thấy hàm số \(y = g\left( x \right)\) có 2 điểm cực đại \(x = 0,\,\,x = 1\).
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\), có đồ thị \(f\left( x \right)\) như hình vẽ. Hàm số \(g\left( x \right) = f\left( {{x^3} + x} \right)\) đạt cực tiểu tại điểm \({x_0}\). Giá trị \({x_0}\) thuộc khoảng nào sau đây?
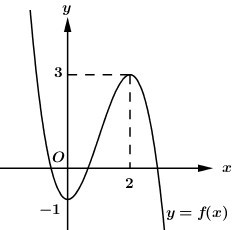
Ta có: \(g\left( x \right) = f\left( {{x^3} + x} \right)\) \( \Rightarrow g'\left( x \right) = \left( {3{x^2} + 1} \right)f'\left( {{x^3} + x} \right)\).
\(g'\left( x \right) = 0 \Leftrightarrow \left( {3{x^2} + 1} \right)f'\left( {{x^3} + x} \right) = 0\) \( \Leftrightarrow f'\left( {{x^3} + x} \right) = 0\).
Dựa vào đồ thị hàm số \(y = f\left( x \right)\) ta thấy hàm số có hai điểm cực trị \(x = 0,\,\,x = 2\).
Do đó \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x^3} + x = 0\\{x^3} + x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\).
Chọn \(x = 2\) ta có \(g'\left( 2 \right) = 13f'\left( {10} \right) < 0\), các nghiệm \(x = 0,\,\,\,x = 1\) là các nghiệm đơn nên qua các nghiệm này \(g'\left( x \right)\) đổi dấu.
BBT:
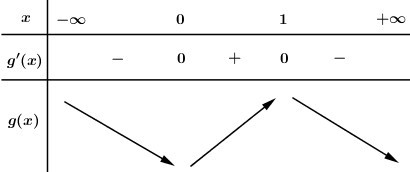
Dựa vào BBT ta thấy điểm cực tiểu của hàm số \(y = g\left( x \right)\) là \({x_0} = 0 \in \left( { - 1;1} \right)\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {{x^2} - 1} \right)\left( {{x^2} - 3x + 2} \right)\). Số điểm cực trị của hàm số đã cho là:
Ta có: \(f'\left( x \right) = \left( {{x^2} - 1} \right)\left( {{x^2} - 3x + 2} \right)\)
\(\begin{array}{l} \Rightarrow f'\left( x \right) = 0\\ \Leftrightarrow \left( {{x^2} - 1} \right)\left( {{x^2} - 3x + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{x^2} - 1 = 0\\{x^2} - 3x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\\x = 1\\x = 2\end{array} \right.\end{array}\)
Ta thấy \(x = 1\) là nghiệm bội 2 của phương trình \(f'\left( x \right) = 0 \Rightarrow x = 1\) không là cực trị của hàm số \(y = f\left( x \right)\)
Vậy hàm số \(y = f\left( x \right)\) có hai điểm cực trị là \(x = - 1\) và \(x = 2.\)
Cho hàm số \(f\left( x \right)\) có bảng biến thiên:

Giá trị cực đại của hàm số đã cho bằng:
Dựa vào BBT ta thấy hàm số có điểm cực đại là \(x = 0\) và giá trị cực đại là: \({y_{CD}} = y\left( 0 \right) = 2.\)
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau :
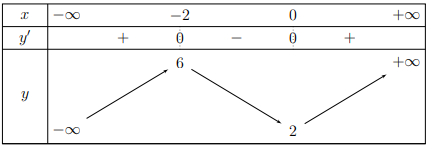
Hàm số \(y = f\left( x \right)\) đạt cực đại tại điểm
Dựa vào BBT ta thấy hàm số \(y = f\left( x \right)\) đạt cực đại tại điểm \(x = - 2\).
Số điểm cực trị của hàm số \(y = \dfrac{{5x - 1}}{{x + 2}}\) là
TXĐ: \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
Ta có \(y = \dfrac{{5x - 1}}{{x + 2}} \Rightarrow y' = \dfrac{{11}}{{{{\left( {x + 2} \right)}^2}}} > 0\,\,\forall x \in D\).
Do đó hàm số đồng biến trên khoảng xác định và không có điểm cực trị nào.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
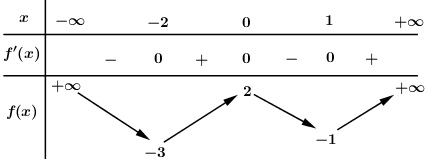
Số điểm cực tiểu của hàm số \(g\left( x \right) = {f^3}\left( x \right) - 3f\left( x \right)\) là:
Ta có:
\(\begin{array}{l}g'\left( x \right) = 3{f^2}\left( x \right).f'\left( x \right) - 3f'\left( x \right)\\g'\left( x \right) = 0\\ \Leftrightarrow 3{f^2}\left( x \right).f'\left( x \right) - 3f'\left( x \right) = 0\\ \Leftrightarrow 3f'\left( x \right).\left[ {{f^2}\left( x \right) - 1} \right] = 0\\ \Leftrightarrow \left[ \begin{array}{l}f'\left( x \right) = 0\\f\left( x \right) = 1\\f\left( x \right) = - 1\end{array} \right.\end{array}\)
Dựa vào BBT ta thấy:
\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 0\\x = 1\end{array} \right.\), qua các nghiệm này \(f'\left( x \right)\) đều đổi dấu.
\(f\left( x \right) = 1\) có 4 nghiệm phân biệt: \(\left[ \begin{array}{l}x = {x_1} \in \left( { - \infty ; - 2} \right)\\x = {x_2} \in \left( { - 2;0} \right)\\x = {x_3} \in \left( {0;1} \right)\\x = {x_4} \in \left( {1; + \infty } \right)\end{array} \right.\).
\(f\left( x \right) = - 1\) có 3 nghiệm phân biệt \(\left[ \begin{array}{l}x = {x_5} \in \left( { - \infty ; - 2} \right),\,\,{x_5} > {x_1}\\x = {x_6} \in \left( { - 2;0} \right),\,\,{x_6} < {x_2}\\x = 1\end{array} \right.\), trong đó
\(x = 1\) là nghiệm kép.
Suy hàm số \(g\left( x \right)\) có 3 + 4 + 2 = 9 điểm cực trị.
Ta có: \(\mathop {\lim }\limits_{x \to \pm \infty } g\left( x \right) = + \infty \) nên số cực tiểu nhiều hơn số cực đại 1 điểm.
Vậy hàm số đã cho có 5 điểm cực tiểu.
Gọi \(A\left( {{x_1};{y_1}} \right),\,B\left( {{x_2};{y_2}} \right)\) là hai điểm cực trị của đồ thị hàm số \(y = \dfrac{1}{3}{x^3} - 4{x^2} - x + 4\). Tính \(P = \dfrac{{{y_1} - {y_2}}}{{{x_1} - {x_2}}}\).
TXĐ: \(D = \mathbb{R}\).
Ta có: \(y' = {x^2} - 8x - 1\)
Lấy \(y\) chia cho \(y'\) ta có: \(y = \left( {\dfrac{1}{3}x - \dfrac{4}{3}} \right).y' - \dfrac{{34}}{3}x + \dfrac{8}{3}\)
Ta có: \(A\left( {{x_1};{y_1}} \right),\,B\left( {{x_2};{y_2}} \right)\) là hai điểm cực trị \(y'\left( {{x_1}} \right) = y'\left( {{x_2}} \right) = 0 \Rightarrow \left\{ \begin{array}{l}{y_1} = - \dfrac{{34}}{3}{x_1} + \dfrac{8}{3}\\{y_2} = - \dfrac{{34}}{3}{x_2} + \dfrac{8}{3}\end{array} \right.\)
Khi đó ta có: \(P = \dfrac{{{y_1} - {y_2}}}{{{x_1} - {x_2}}} = \dfrac{{ - \dfrac{{34}}{3}{x_1} + \dfrac{8}{3} + \dfrac{{34}}{3}{x_2} - \dfrac{8}{3}}}{{{x_1} - {x_2}}} \)\(= \dfrac{{ - \dfrac{{34}}{3}\left( {{x_1} - {x_2}} \right)}}{{{x_1} - {x_2}}} = - \dfrac{{34}}{3}\)
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\). Đồ thị hàm số \(y = f'\left( x \right)\) như hình bên. Hàm số \(y = f\left( {{x^2} + 4x} \right) - {x^2} - 4x\) có bao nhiêu điểm cực trị thuộc khoảng \(\left( { - 5;1} \right)\)?
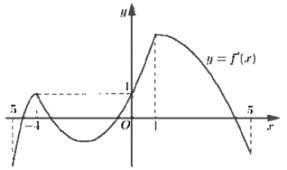
Ta có:
\(\begin{array}{l}y' = \left( {2x + 4} \right)f'\left( {{x^2} + 4x} \right) - 2x - 4\\ = \left( {2x + 4} \right)\left[ {f'\left( {{x^2} + 4x} \right) - 1} \right]\\y' = 0 \Leftrightarrow \left[ \begin{array}{l}2x + 4 = 0\\f'\left( {{x^2} + 4x} \right) - 1 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}2x + 4 = 0\\f'\left( {{x^2} + 4x} \right) = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x + 4 = 0\\{x^2} + 4x = - 4\\{x^2} + 4x = 0\\{x^2} + 4x = t \in \left( {1;5} \right)\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = - 2 \in \left( { - 5;1} \right)\,\,\left( {\text{bội }\,\,3} \right)\\x = 0 \in \left( { - 5;1} \right)\\x = - 4 \in \left( { - 5;1} \right)\\x = - 2 \pm \sqrt {4 + t} \end{array} \right.\end{array}\)
Xét \({x_1} = - 2 - \sqrt {4 + t} \), với \(1 < t < 5\) thì \( - 5 < - 2 - \sqrt {4 + t} < - 2 - \sqrt 5 < 1\) \( \Rightarrow - 5 < {x_1} < 1\)
Xét \({x_2} = - 2 + \sqrt {4 + t} \), với \(1 < t < 5\) thì \( - 5 < - 2 + \sqrt 5 < - 2 + \sqrt {4 + t} < 1\) \( \Rightarrow - 5 < {x_2} < 1\)
Do đó phương trình \(y' = 0\) có \(5\) nghiệm phân biệt thuộc \(\left( { - 5;1} \right)\) và các nghiệm này đều là nghiệm bội lẻ nên đạo hàm \(y'\) đổi dấu qua chúng.
Vậy hàm số có \(5\) điểm cực trị trong khoảng \(\left( { - 5;1} \right)\)

