Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu đạo hàm như hình bên. Số điểm cực trị của hàm số đã cho là:
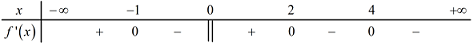
Dựa vào bảng xét dấu ta thấy \(f'\left( x \right)\) đổi dấu qua \(x = - 1,\,\,\,x = 0\) và \(x = 2\) nên hàm số có 3 điểm cực trị.
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên đoạn \(\left[ { - 2;2} \right]\) và có đồ thị là đường cong trong hình vẽ bên. Hàm số \(f\left( x \right)\) đạt cực tiểu tại điểm nào dưới đây?
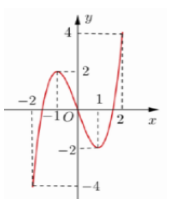
Hàm số \(f\left( x \right)\) đạt cực tiểu tại điểm \(x = 1\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ { - 3;3} \right]\) và có bảng xét dấu của đạo hàm như hình bên:

Mệnh đề nào sau đây sai?
Dựa vào BBT, ta thấy hàm số đạt cực đại tại \(x = - 1\) và \(x = 2.\)
Hàm số đạt cực tiểu tại \(x = 1.\)
Tại \(x = 0,\) \(f'\left( x \right)\) không đổi dấu nên \(x = 0\) không là cực trị của hàm số.
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có bảng xét dấu đạo hàm như sau:
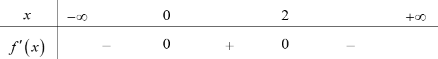
Tổng giá trị tất cả các điểm cực trị của hàm số \(y = f\left( {x - 2019} \right) + 2020\) là:
Dựa vào BBT ta thấy hàm số \(y = f\left( x \right)\) đồng biến trên \(\left( {0;\,2} \right)\) và nghịch biến trên \(\left( { - \infty ;\,\,0} \right),\,\,\left( {2; + \infty } \right).\)
Hàm số \(y = f\left( x \right)\) có hai điểm cực trị là: \(x = 0,\,\,x = 2.\)
Xét hàm số \(y = f\left( {x - 2019} \right) + 2020\) ta có:
\(\begin{array}{l}y' = f'\left( {x - 2019} \right) \Rightarrow y' = 0 \Leftrightarrow f'\left( {x - 2019} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 2019 = 0\\x - 2019 = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2019\\x = 2021\end{array} \right.\end{array}\)
Ta có bảng xét dấu:
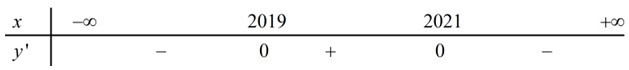
\( \Rightarrow \) Hàm số \(y = f\left( {x - 2019} \right) + 2020\) có hai điểm cực trị là \(x = 2019,\,\,\,x = 2020\)
\( \Rightarrow 2019 + 2021 = 4040.\)
Số điểm cực trị của hàm số \(y = \left| {\left( {x - 1} \right){{\left( {x - 2} \right)}^2}} \right|\) là:
Xét hàm số \(y = \left( {x - 1} \right){\left( {x - 2} \right)^2} = {x^3} - 5{x^2} + 8x - 4\).
TXĐ: \(D = \mathbb{R}\).
Ta có \(y' = 3{x^2} - 10x + 8\).
\(y' = 0 \Leftrightarrow 3{x^2} - 10x + 8 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = \dfrac{4}{3}\end{array} \right.\)
BBT:
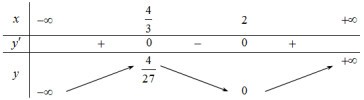
Từ BBT của đồ thị hàm số \(y = \left( {x - 1} \right){\left( {x - 2} \right)^2}\) ta suy ra BBT của đồ thị hàm số \(y = \left| {\left( {x - 1} \right){{\left( {x - 2} \right)}^2}} \right|\) như sau:
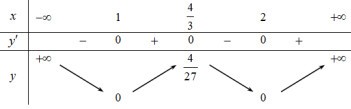
Từ BBT ta thấy hàm số \(y = \left| {\left( {x - 1} \right){{\left( {x - 2} \right)}^2}} \right|\) có 3 điểm cực trị.
Đề thi THPT QG 2020 – mã đề 104
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
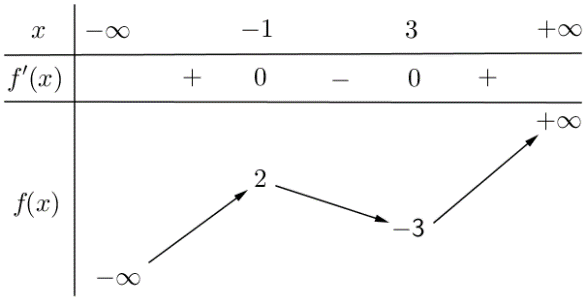
Giá trị cực đại của hàm số đã cho bằng
Dựa vào BBT ta thấy hàm số đã cho đạt cực đại tại \(x = - 1\) và giá trị cực đại là \({y_{CD}} = 2.\)
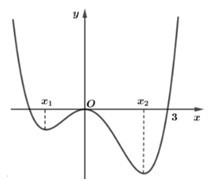
Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình dưới đây:
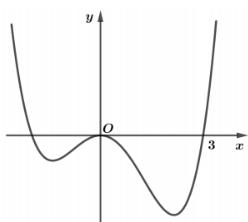
Số điểm cực trị của hàm số \(g\left( x \right) = f\left( {{x^3} - 3{x^2}} \right)\) là:
Ta có: \(g'\left( x \right) = \left( {3{x^2} - 6x} \right)f'\left( {{x^3} - 3{x^2}} \right)\).
Khi đó \(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\\f'\left( {{x^3} - 3{x^2}} \right) = 0\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\,\,\left( {\text{bội }\,\,3} \right)\\x = 2\\x = 3\\{x^3} - 3{x^2} = {x_1} \in \left( { - 3;0} \right)\,\,\,\left( 1 \right)\\{x^3} - 3{x^2} = {x_2} \in \left( {0;3} \right)\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\).
Xét hàm số \(h\left( x \right) = {x^3} - 3{x^2}\) ta có \(h'\left( x \right) = 3{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\).
BBT:
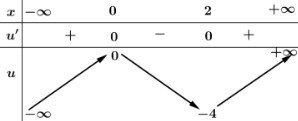
Dựa vào BBT ta thấy:
- Phương trình (1) có 3 nghiệm phân biệt.
- Phương trình (2) có 1 nghiệm.
Suy ra phương trình \(g'\left( x \right) = 0\) có tất cả 7 nghiệm bội lẻ.
Vậy hàm số \(g\left( x \right) = f\left( {{x^3} - 3{x^2}} \right)\) có 7 điểm cực trị.
Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình bên. Số điểm cực trị của hàm số \(g\left( x \right) = f\left( {{x^3} + 3{x^2}} \right)\) là:
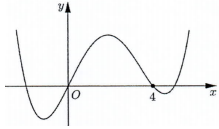
Ta có: \(g'\left( x \right) = \left( {3{x^2} + 6x} \right)f'\left( {{x^3} + 3{x^2}} \right)\).
Cho \(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}3{x^2} + 6x = 0\\f'\left( {{x^3} + 3{x^2}} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 2\\f'\left( {{x^3} + 3{x^2}} \right) = 0\,\,\,\left( * \right)\end{array} \right.\)
Dựa vào đồ thị hàm số ta thấy phương trình (*) tương đương với: \(\left[ \begin{array}{l}{x^3} + 3{x^2} = a < 0\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\{x^3} + 3{x^2} = b \in \left( {0;4} \right)\,\,\,\left( 2 \right)\\{x^3} + 3{x^2} = c < 0\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right)\end{array} \right.\)
Xét hàm số \(y = {x^3} + 3{x^2}\) ta có: \(y' = 3{x^2} + 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 2\end{array} \right.\).
BBT:
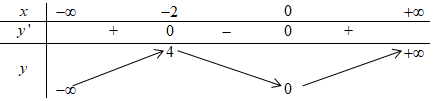
Dựa vào BBT ta thấy:
+ Phương trình (1) có 1 nghiệm khác \(0; - 2.\)
+ Phương trình (2) có 3 nghiệm phân biệt khác \(0; - 2.\)
+ Phương trình (3) có 1 nghiệm khác \(0; - 2.\)
Do đó phương trình \(f'\left( x \right) = 0\) có 7 nghiệm đơn phân biệt.
Vậy hàm số \(y = g\left( x \right)\) có 7 cực trị.
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ bên.

Hàm số \(y = f\left( {{x^2} - 1} \right)\) có bao nhiêu điểm cực trị?
Đặt \(y = g\left( x \right) = f\left( {{x^2} - 1} \right)\).
Ta có : \(g'\left( x \right) = \left( {{x^2} - 1} \right)'.f'\left( {{x^2} - 1} \right) = 2x.f'\left( {{x^2} - 1} \right)\)
Cho \(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\f'\left( {{x^2} - 1} \right) = 0\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} - 1 = - 1\\{x^2} - 1 = 1\\{x^2} - 1 = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt 2 \\x = \pm \sqrt 5 \end{array} \right.\)
(Tất cả các nghiệm trên đều là nghiệm bội lẻ).
Bảng xét dấu \(g'\left( x \right)\):

Vậy, hàm số \(y = f\left( {{x^2} - 1} \right)\) có tất cả 5 điểm cực trị.
Cho hàm số \(\left[ { - 1;3} \right]\) có bảng biến thiên như hình vẽ dưới đây. Hàm số đạt cực tiểu tại điểm nào trong các điểm sau?
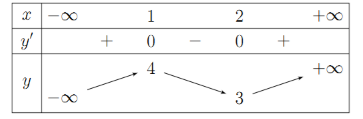
Hàm số đạt cực tiểu tại điểm \(x = 2\).
Đề thi THPT QG 2020 – mã đề 104
Cho hàm số \(f\left( x \right)\) liên tục trên R có bảng xét dấu \(f'\left( x \right)\)
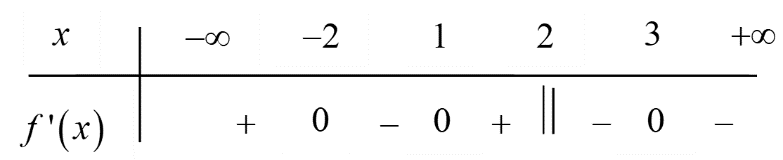
Số điểm cực đại của hàm số đã cho là:
Dựa vào BBT ta thấy, \(f'\left( x \right)\) đổi dấu từ dương sang âm hai lần
\( \Rightarrow \) Hàm số có hai điểm cực đại.
Hàm số nào sau đây không có điểm cực trị?
Xét đáp án A ta có \(y' = 3{x^2} + 3 > 0\,\,\forall x \in \mathbb{R} \Rightarrow \) Hàm số không có cực trị.
Nếu ${x_0}$ là điểm cực đại của hàm số thì $\left( {{x_0};f\left( {{x_0}} \right)} \right)$ là:
Nếu ${x_0}$ là điểm cực đại của hàm số thì $\left( {{x_0};f\left( {{x_0}} \right)} \right)$ là điểm cực đại của đồ thị hàm số.
Cho các phát biểu sau:
1. Hàm số $y = f\left( x \right)$ đạt cực đại tại ${x_0}$ khi và chỉ khi đạo hàm đổi dấu từ dương sang âm qua ${x_0}$.
2. Hàm số $y = f\left( x \right)$ đạt cực trị tại ${x_0}$ khi và chỉ khi ${x_0}$ là nghiệm của đạo hàm.
3. Nếu $f'\left( {{x_0}} \right) = 0$ và $f''\left( {{x_0}} \right) = 0$ thì ${x_0}$ không phải là cực trị của hàm số $y = f\left( x \right)$ đã cho.
4. Nếu $f'\left( {{x_0}} \right) = 0$ và $f''\left( {{x_o}} \right) > 0$ thì hàm số đạt cực đại tại ${x_0}$.
Các phát biểu đúng là:
+) Ta có định lí: Nếu $f'\left( x \right)$ đổi dấu từ dương sang âm khi $x$ qua điểm ${x_o}$ (theo chiều tăng) thì hàm số đạt cực đại tại điểm ${x_o}$ $ \Rightarrow $ 1 đúng.
+) Điều kiện cần để ${x_o}$ là điểm cực trị của hàm số là: ${x_o}$ là nghiệm của phương trình $f'\left( x \right) = 0$$ \Rightarrow $ 2 sai.
+) Nếu $f'\left( {{x_o}} \right) = 0$ và $f\left( x \right)$ có đạo hàm cấp hai khác 0 tại điểm ${x_o}$ thì:
-) Nếu $f''\left( {{x_o}} \right) < 0$ thì hàm số $f\left( x \right)$ đạt cực đại tại điểm ${x_o}$.
-) Nếu $f''\left( {{x_o}} \right) > 0$ thì hàm số $f\left( x \right)$ đạt cực tiểu tại điểm ${x_o}$.
+) Nếu $f'\left( {{x_o}} \right) = 0$ và $f''\left( {{x_o}} \right) = 0$ thì ta không kết luận gì chứ không phải hàm số không đạt cực trị tại ${x_0}$.
Khi \(\left\{ \begin{array}{l}f'\left( {{x_0}} \right) = 0\\f''\left( {{x_0}} \right) = 0\end{array} \right.\) thì ta không kết luận gì vì có thể xảy ra cả hai trường hợp là hàm số đạt cực trị hoặc không đạt cực trị tại \({x_0}\).
Ví dụ:
+) TH1: Xét hàm \(f\left( x \right) = {x^4}\) có \(f'\left( x \right) = 4{x^3} = 0 \Leftrightarrow x = 0\)
\(f''\left( x \right) = 12{x^2}\) và \(f''\left( 0 \right) = 0\).
Trong TH này hàm số có \(f''\left( 0 \right) = 0\) nhưng vẫn đạt cực tiểu tại \(x = 0\) vì đạo hàm \(f'\left( x \right)\) đổi dấu từ âm sang dương qua \(x = 0\).
+) TH2: Xét hàm \(g\left( x \right) = {x^3}\) có \(f'\left( x \right) = 3{x^2} = 0 \Leftrightarrow x = 0\)
\(f''\left( x \right) = 6x \Rightarrow f''\left( 0 \right) = 0\)
Trong TH này hàm số có \(f''\left( 0 \right) = 0\) nhưng không đạt cực trị tại \(x = 0\) vì đạo hàm \(f'\left( x \right) = 3{x^2}\) không đổi dấu của \(x = 0\).
$ \Rightarrow $ 3 và 4 sai.
Điều kiện để hàm số bậc ba không có cực trị là phương trình $y' = 0$ có:
Điều kiện để hàm số bậc ba không có cực trị là phương trình $y' = 0$ vô nghiệm hoặc có nghiệm kép.
Chọn phát biểu đúng:
Hàm số bậc ba chỉ có thể có $2$ cực trị hoặc không có cực trị nào nên nếu nó có cực đại thì chắc chắn sẽ có cực tiểu và ngược lại nên A, B sai.
Không phải lúc nào hàm bậc ba cũng có $2$ cực trị, vẫn có trường hợp không có cực trị nên D sai.
Số điểm cực trị của đồ thị hàm số $y = \dfrac{{x - 1}}{{2 - x}}$ là:
TXĐ: $D = R\backslash \left\{ 2 \right\}$
Dễ thấy $y' = \dfrac{1}{{{{\left( {2 - x} \right)}^2}}} > 0$ $\forall x \in D$
$ \Rightarrow $ Hàm số đồng biến trên các khoảng $\left( -\infty ;2 \right)$ và $\left( 2;+\infty \right)$
$ \Rightarrow $ Hàm số không có cực trị.
Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y = {x^3} - 3{x^2} + 1$ là:
Cách 1:
$y' = 3{x^2} - 6x$ ;
$y' = 0 \Leftrightarrow 3x\left( {x - 2} \right) = 0 \Leftrightarrow \left[ \begin{gathered}x = 0 \Rightarrow y = 1 \hfill \\x = 2 \Rightarrow y = - 3 \hfill \\ \end{gathered} \right.$
Từ đây suy ra hai điểm cực trị có tọa độ $A\left( {0,1} \right)$ và $B\left( {2, - 3} \right).$
Phương trình đường thẳng qua hai điểm $A, B$ là: $\dfrac{{x - 0}}{{2 - 0}} = \dfrac{{y - 1}}{{ - 3 - 1}}$ $\Leftrightarrow - 4x = 2\left( {y - 1} \right) \Leftrightarrow y = - 2x + 1.$
Cách 2:
Ta có $y' = 3{x^2} - 6x$
Khi đó ${x^3} - 3{x^2} + 1 $ $= \left( {3{x^2} - 6x} \right)\left( {\dfrac{1}{3}x - \dfrac{1}{3}} \right) - 2x + 1$
Vậy đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là $y = - 2x + 1$
Cách 3:
Bước 1:
$y'=3x^2-6x$; $y''=6x-6$
Bước 2:
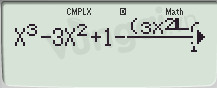
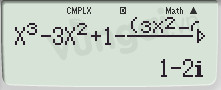
Bước 3: Ta được a=1 và b=-2
Vậy đường thẳng là: $y=-2x+1$
Hàm số nào sau đây không có cực trị?
Đáp án A: $y' = 3{x^2} \ge 0 $ với mọi \(x\) nên hàm số đồng biến trên \(R\). Do đó nó không có cực trị.
Vậy hàm số $y = {x^3}$ không có cực trị.
Đáp án B: $y' = 3{x^2} + 6x = 3x\left( {x + 2} \right) = 0 \Leftrightarrow \left[ \begin{gathered}x = 0 \hfill\\x = - 2 \hfill \\ \end{gathered} \right.$ $y'' = 6x + 6 \Rightarrow \left\{ \begin{gathered} y''\left( 0\right) = 6 > 0 \hfill \\ y''\left( { - 2} \right) = - 6 < 0 \hfill \\ \end{gathered} \right.$, do đó $x = 0$ là điểm cực tiểu của hàm số, $x = - 2$ là điểm cực đại của hàm số.
Đáp án C: $y' = 4{x^3} = 0 \Leftrightarrow x = 0 \Rightarrow \left\{ \begin{gathered} y' > 0,\forall x > 0\hfill \\ y' < 0,\forall x < 0 \hfill \\ \end{gathered} \right. \Rightarrow x = 0$ là điểm cực tiểu của hàm số.
Đáp án D: $y' = 4{x^3} = 0 \Leftrightarrow x = 0 \Rightarrow \left\{ \begin{gathered}y' > 0,\forall x > 0 \hfill \\ y' < 0,\forall x < 0 \hfill \\ \end{gathered} \right. \Rightarrow x = 0$ là điểm cực tiểu của hàm số.
Hàm số $f\left( x \right) = 2\sin 2x - 3$ đạt cực tiểu tại:
Ta có: $f\left( x \right) = 2\sin 2x - 3$
TXĐ: $D = R.$
$f'\left( x \right) = 4\cos 2x$, $f'\left( x \right) = 0 \Leftrightarrow \cos 2x = 0 \Leftrightarrow 2x =\dfrac{\pi }{2} + k\pi $ $\Leftrightarrow x = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}$, $k \in Z$
$f''\left( x \right) = - 8\sin 2x$
Ta có: $f''\left( {\dfrac{\pi }{4} + \dfrac{{k\pi }}{2}} \right) = - 8\sin \left( {\dfrac{\pi }{2} + k\pi } \right) $ , $k \in Z$
Khi $k=2n$ thì \(\sin \left( {\dfrac{\pi }{2} + 2n\pi } \right) = \sin \dfrac{\pi }{2} = 1\) nên \(f''\left( {\dfrac{\pi }{4} + \dfrac{{2n\pi }}{2}} \right) = - 8 < 0\)
Khi $k=2n+1$ thì \(\sin \left( {\dfrac{\pi }{2} + \left( {2n + 1} \right)\pi } \right) = \sin \dfrac{{3\pi }}{2} = - 1\) nên \(f''\left( {\dfrac{\pi }{4} + \dfrac{{\left( {2n + 1} \right)\pi }}{2}} \right) = 8 > 0\)
Vậy hàm số đạt cực tiểu tại $x = \dfrac{\pi }{4} + \dfrac{\left( {2k + 1}\right)\pi }{2} $

