Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như hình vẽ:
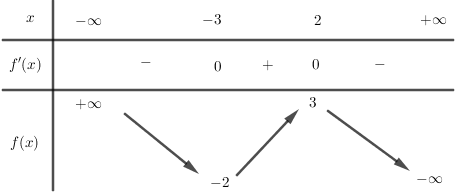
Trong các khẳng định sau, khẳng định nào đúng?
Nhận thấy hàm số nghịch biến trên các khoảng $\left( { - \infty ; - 3} \right)$ và $\left( {2; + \infty } \right)$
Hàm số có giá trị cực đại bằng 3 tại $x = 2$
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:
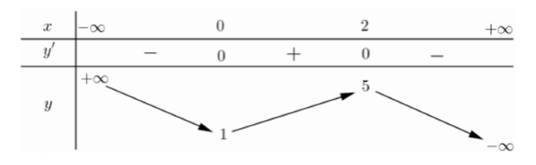
Hàm số đạt cực đại tại điểm
Quan sát bảng biến thiên ta thấy hàm số đạt tiểu tại điểm $x = 0$ và đạt cực đại tại điểm $x = 2$ .
Cho hàm số y = f (x) có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?
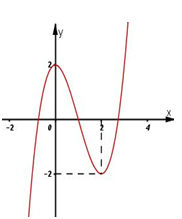
Dựa vào đồ thị hàm số ta thấy hàm số có 2 điểm cực trị suy ra Loại đáp án D.
Hàm số đạt cực tiểu tại x = 2 và đạt cực đại tại x = 0. Suy ra Đáp án B đúng.
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:
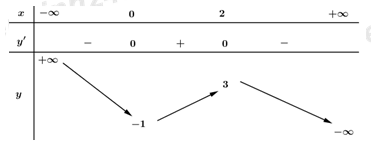
Hàm số đạt cực đại tại điểm:
Dựa vào đồ thị hàm số ta thấy hàm số đạt cực đại tại điểm $x = 2.$
Điểm cực tiểu của đồ thị hàm số $y = {x^3} - 3x + 5$ là điểm
Có $y' = 3{x^2} - 3 = 0 \Leftrightarrow x = {\rm{\;}} \pm 1$
Vì hệ số của ${x^3}$ là dương nên đồ thị hàm số có điểm cực tiểu $\left( {1;3} \right)$
Cho hàm số $y = \dfrac{{{x^2} - ax + b}}{{x - 1}}$. Đặt $A = a - b,B = a + 2b$. Để đồ thị hàm số có điểm cực đại $C\left( {0; - 1} \right)$ thì tổng giá trị của $A + 2B$ là:
Ta có:
$y' = f'\left( x \right) = \dfrac{{\left( {2x - a} \right)\left( {x - 1} \right) - \left( {{x^2} - ax + b} \right)}}{{{{\left( {x - 1} \right)}^2}}}$ $ = \dfrac{{{x^2} - 2x + a - b}}{{{{\left( {x - 1} \right)}^2}}}$
Vì $C\left( {0; - 1} \right)$ là điểm cực đại của đồ thị hàm số nên:$\left\{ {\begin{array}{*{20}{l}}{f'\left( 0 \right) = 0}\\{f\left( 0 \right) = - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a - b = 0}\\{ - b = - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = 1}\end{array}} \right.$
Thay $a = 1,b = 1$ vào hàm số ta thấy điểm $C\left( {0; - 1} \right)$ là điểm cực đại của đồ thị hàm số.
Vậy $a = b = 1 \Rightarrow A + 2B = 6$.
Cho hàm bậc bốn $y = f\left( x \right)$. Hàm số $y = f'\left( x \right)$ có đồ thị như hình bên. Số điểm cực đại của hàm số $f\left( {\sqrt {{x^2} + 2x + 2} } \right)$ là
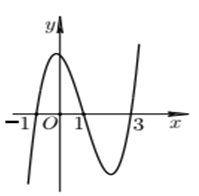
Quan sát đồ thị hàm số $y = f'\left( x \right)$ ta thấy $f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\\x = 3\end{array} \right.$
Đặt $g\left( x \right) = f\left( {\sqrt {{x^2} + 2x + 2} } \right) \Rightarrow g'\left( x \right) = \frac{{x + 1}}{{\sqrt {{x^2} + 2x + 2} }}f'\left( {\sqrt {{x^2} + 2x + 2} } \right)$
\(\begin{array}{*{20}{l}}{g'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x + 1 = 0}\\{f'\left( {\sqrt {{x^2} + 2x + 2} } \right) = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 1}\\{\sqrt {{x^2} + 2x + 2} = - 1{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {vn} \right)}\\{\sqrt {{x^2} + 2x + 2} = 1{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 1 \right)}\\{\sqrt {{x^2} + 2x + 2} = 3{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 2 \right)}\end{array}} \right.}\\{\left( 1 \right) \Leftrightarrow {x^2} + 2x + 2 = 1 \Leftrightarrow {x^2} + 2x + 1 = 0 \Leftrightarrow {{\left( {x + 1} \right)}^2} = 0 \Leftrightarrow x = - 1}\\{\left( 2 \right) \Leftrightarrow {x^2} + 2x + 2 = 9 \Leftrightarrow x = - 1 \pm 2\sqrt 2 }\end{array}\)
Nghiệm của phương trình (1) là nghiệm bội 2 nên không là cực trị của hàm số $y = g\left( x \right) = f\left( {\sqrt {{x^2} + 2x + 2} } \right)$. Lập BBT của hàm số $y = g\left( x \right)$:
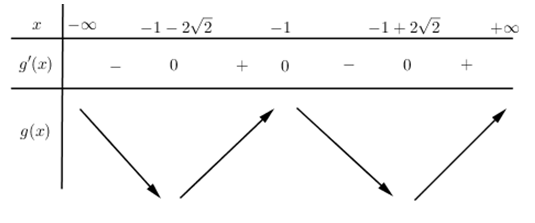
Dựa vào BBT ta thấy hàm số $y = g\left( x \right)$ đạt cực đại tại $x = - 1$.
Cho hàm số bậc ba $y = f\left( x \right)$ có đồ thị như hình vẽ
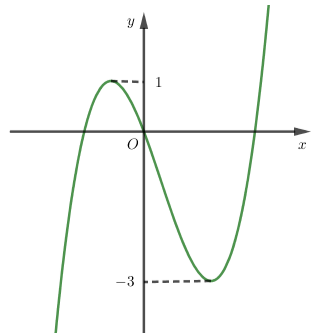
Tìm tất cả các giá trị của $m\;$ để hàm số $y = \left| {f\left( x \right) + m} \right|$ có ba điểm cực trị.
Đồ thị hàm số $y = f\left( x \right) + m$ có được bằng cách tịnh tiến đồ thị hàm số $y = f\left( x \right)$ theo phương của trục $Oy$ $m$ đơn vị (lên trên hay xuống dưới phụ thuộc vào \(m\) dương hay âm), do đó nó đồ thị hàm số $y = f\left( x \right) + m$ có ${y_{CD}} = 1 + m;{\mkern 1mu} {\mkern 1mu} {y_{CT}} = - 3 + m$
Lấy đối xứng phần dưới của đồ thị hàm số \(y = f\left( x \right) + m\) qua \(Ox\) ta được đồ thị hàm số \(y = \left| {f\left( x \right) + m} \right|\)
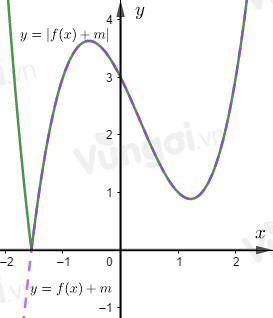
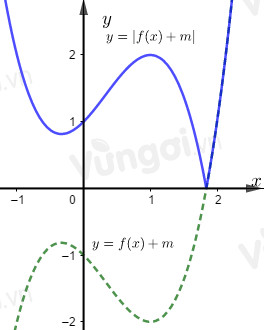
Để đồ thị hàm số $y = \left| {f\left( x \right) + m} \right|$ có ba điểm cực trị thì đồ thị hàm số \(y=f\left( x \right) + m\) cắt trục \(Ox\) tại đúng một điểm tức là điểm cực tiểu nằm trên trục \(Ox\) hoặc điểm cực đại nằm dưới trục \(Ox\), hay:
$\left[ {\begin{array}{*{20}{l}}{{y_{CT}} = {\rm{\;}} - 3 + m \ge 0}\\{{y_{CD}} = 1 + m \le 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m \ge 3}\\{m \le {\rm{\;}} - 1}\end{array}} \right.$
Đề thi THPT QG - 2021 - mã 103
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng:
Hàm số đạt cực đại tại \(x = 0\), giá trị cực đại bằng \(3\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
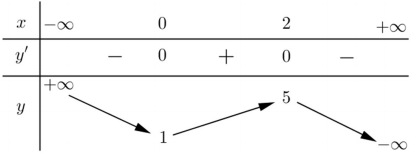
Giá trị cực đại của hàm số đã cho bằng:
Quan sát bảng biến thiên ta thấy hàm số đạt cực đại tại điểm \(x = 2\) và giá trị cực đại của hàm số yCĐ = 5.
Đề thi THPT QG 2019 – mã đề 104
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau :
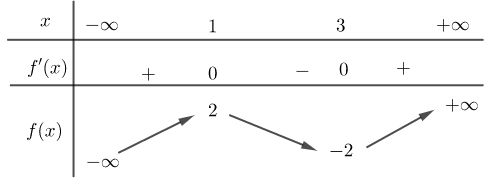
Hàm số đã cho đạt cực tiểu tại
Dựa vào đồ thị hàm số ta thấy hàm số đã cho đạt cực tiểu tại \(x = 3\).
Khoảng cách từ điểm cực tiểu của đồ thị hàm số \(y={{x}^{3}}-3{{x}^{2}}+2\) đến trục tung bằng
Ta có \(y={{x}^{3}}-3{{x}^{2}}+2\,\,\xrightarrow{{}}\,\,{y}'=3{{x}^{2}}-6x;\,\,{y}'=0\Leftrightarrow \left[\begin{align} x=0\,\,\Rightarrow y\left( 0 \right)=2 \\ x=2\,\,\Rightarrow \,\,y\left( 2 \right)=-\,2 \\\end{align} \right..\)
Suy ra điểm cực tiểu của đồ thị hàm số là \(M\left( 2;-\,2 \right).\)
Vậy \(d\left( M;\left( Oy \right) \right)=2.\)
Đề thi THPT QG 2019 – mã đề 104
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x{\left( {x + 1} \right)^2},\forall x \in \mathbb{R}.\) Số điểm cực trị của hàm số đã cho là
\(f'\left( x \right) = x{\left( {x + 1} \right)^2} \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\left( {boi\,\,1} \right)\\x = - 1\,\,\left( {boi\,\,2} \right)\end{array} \right..\)
Vậy hàm số đã cho có 1 điểm cực trị.
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
Ta có tại điểm cực tiểu \(x = 0\), hàm số có giá trị \(y = 1\)
Đề thi THPT QG - 2021 - mã 101
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
Do \(y'\) đổi dấu 4 lần nên hàm số có 4 điểm cực trị.
Đề thi THPT QG 2019 – mã đề 104
Cho hàm số \(f\left( x \right)\), bảng biến thiên của hàm số \(f'\left( x \right)\)như sau:
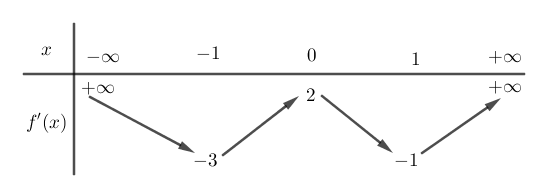
Số điểm cực trị của hàm số \(y = f\left( {4{x^2} + 4x} \right)\) là:
Ta có: \(y' = \left( {8x + 4} \right)f'\left( {4{x^2} + 4x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{1}{2}\\f'\left( {4{x^2} + 4x} \right) = 0\end{array} \right.\).
\(f'\left( {4{x^2} + 4x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}4{x^2} + 4x = {x_1}\,\,\left( {{x_1} < - 1} \right)\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\4{x^2} + 4x = {x_2}\,\,\left( { - 1 < {x_2} < 0} \right)\,\,\left( 2 \right)\\4{x^2} + 4x = {x_3}\,\,\left( {0 < {x_3} < 1} \right)\,\,\,\,\,\,\left( 3 \right)\\4{x^2} + 4x = {x_4}\,\,\left( {1 < {x_4}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 4 \right)\end{array} \right.\)
Xét phương trình \(4{x^2} + 4x = {x_i} \Leftrightarrow 4{x^2} + 4x - {x_i} = 0\,\,\left( * \right)\) ta có: \(\Delta ' = 4 + 4{x_i}\).
+) \(\Delta ' < 0 \Leftrightarrow 4 + 4{x_i} < 0 \Leftrightarrow {x_i} < - 1 \Rightarrow \) Phương trình vô nghiệm.
+) \(\Delta ' = 0 \Leftrightarrow {x_i} = - 1 \Rightarrow \) Phương trình có nghiệm kép \(x = - \dfrac{1}{2}\).
+) \(\Delta ' > 0 \Leftrightarrow {x_i} > - 1 \Rightarrow \) Phương trình có 2 nghiệm phân biệt \(x \ne - \dfrac{1}{2}\).
Do đó:
Phương trình (1) vô nghiệm.
Phương trình (2, (3), (4) có 2 nghiệm phân biệt \(x \ne - \dfrac{1}{2}\).
Vậy phương trình \(y' = 0\) có 7 nghiệm đơn phân biệt hay hàm số \(y = f\left( {4{x^2} + 4x} \right)\) có 7 cực trị.
Cho hàm số \(y = f(x)\) có bảng xét dấu của đạo hàm như sau:
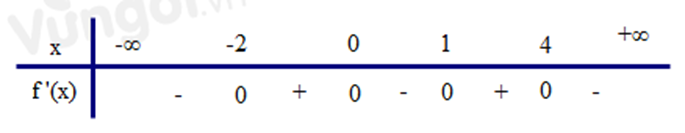
Số điểm cực trị của hàm số đã cho là
Từ bảng xét dấu, ta có: số điểm cực trị của hàm số đã cho là 4 .
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(f\left( x \right)\) có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
Ta có \(f'\left( x \right)\) đổi dấu qua \(x = - 2;\,\,x = - 1;\,\,x = 2;\,\,x = 4\) nên hàm số có \(4\) điểm cực trị.
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x\left( {x - 1} \right){\left( {x + 2} \right)^3};\,\forall x \in \mathbb{R}.\) Số điểm cực trị của hàm số đã cho là
Ta có \(f'\left( x \right) = 0 \Leftrightarrow x\left( {x - 1} \right){\left( {x + 2} \right)^3} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x = - 2\end{array} \right.\) và các nghiệm này đều là nghiệm bội bậc lẻ nên hàm số đã cho có ba điểm cực trị.
Cho hàm số \(f\left( x \right) = {x^2}\left( {x - 1} \right){e^{3x}}\) có một nguyên hàm là hàm số \(F\left( x \right).\) Số cực trị của hàm số \(F\left( x \right)\) là
Vì hàm số \(f\left( x \right) = {x^2}\left( {x - 1} \right){e^{3x}}\) có một nguyên hàm là hàm số \(F\left( x \right)\) nên \(F'\left( x \right) = f\left( x \right) = {x^2}\left( {x - 1} \right){e^{3x}}\)
Xét \(F'\left( x \right) = 0 \Leftrightarrow {x^2}\left( {x - 1} \right){e^{3x}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\)
Bảng biến thiên của hàm \(F\left( x \right).\)
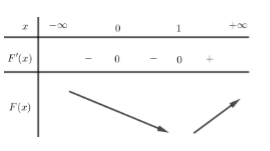
Vậy hàm số có 1 điểm cực trị.

