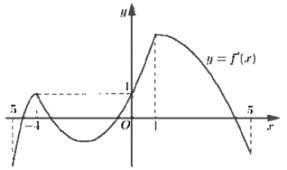
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\). Đồ thị hàm số \(y = f'\left( x \right)\) như hình bên. Hàm số \(y = f\left( {{x^2} + 4x} \right) - {x^2} - 4x\) có bao nhiêu điểm cực trị thuộc khoảng \(\left( { - 5;1} \right)\)?

Ta có:

\(\begin{array}{l}y' = \left( {2x + 4} \right)f'\left( {{x^2} + 4x} \right) - 2x - 4\\ = \left( {2x + 4} \right)\left[ {f'\left( {{x^2} + 4x} \right) - 1} \right]\\y' = 0 \Leftrightarrow \left[ \begin{array}{l}2x + 4 = 0\\f'\left( {{x^2} + 4x} \right) - 1 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}2x + 4 = 0\\f'\left( {{x^2} + 4x} \right) = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x + 4 = 0\\{x^2} + 4x =  - 4\\{x^2} + 4x = 0\\{x^2} + 4x = t \in \left( {1;5} \right)\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x =  - 2 \in \left( { - 5;1} \right)\,\,\left( {\text{bội }\,\,3} \right)\\x = 0 \in \left( { - 5;1} \right)\\x =  - 4 \in \left( { - 5;1} \right)\\x =  - 2 \pm \sqrt {4 + t} \end{array} \right.\end{array}\)

Xét \({x_1} =  - 2 - \sqrt {4 + t} \), với \(1 < t < 5\) thì \( - 5 <  - 2 - \sqrt {4 + t}  <  - 2 - \sqrt 5  < 1\) \( \Rightarrow  - 5 < {x_1} < 1\)

Xét \({x_2} =  - 2 + \sqrt {4 + t} \), với \(1 < t < 5\) thì \( - 5 <  - 2 + \sqrt 5  <  - 2 + \sqrt {4 + t}  < 1\) \( \Rightarrow  - 5 < {x_2} < 1\)

Do đó phương trình \(y' = 0\) có \(5\) nghiệm phân biệt thuộc \(\left( { - 5;1} \right)\) và các nghiệm này đều là nghiệm bội lẻ nên đạo hàm \(y'\) đổi dấu qua chúng.

Vậy hàm số có \(5\) điểm cực trị trong khoảng \(\left( { - 5;1} \right)\)