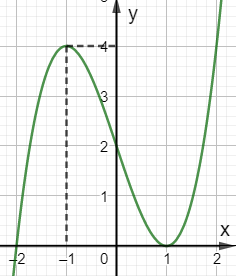
Cho hàm số \(y = f(x)\) có đồ thị hàm số \(y = {f^\prime }(x)\) như hình bên dưới. Tìm số điểm cực trị của hàm số \(g(x) = f\left( {{x^2} - 3} \right)\).
Trả lời bởi giáo viên
Bước 1: Tìm nghiệm của phương trình y’=0
Từ đồ thị hàm số ta có \(f'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 2}\\{x = 1}\end{array}} \right.\).
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{{x^2} - 3 = - 2}\\{{x^2} - 3 = 1{\text{ (nghiệm kép) }}}\end{array}} \right.\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = \pm 1}\\{x = \pm 2{\text{ (nghiệm kép) }}}\end{array}} \right.\)
Bước 2: Lập bảng biến thiên và tìm số cực trị
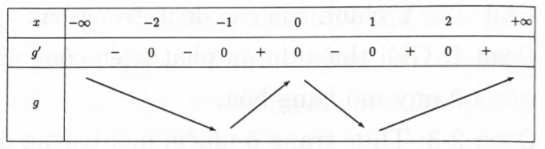
Dựa vào bảng biến thiên ta thấy hàm số có 3 điểm cực trị.
Hướng dẫn giải:
Bước 1: Tìm nghiệm của phương trình y’=0
Bước 2: Lập bảng biến thiên và tìm số cực trị

