Các dạng toán viết phương trình mặt phẳng

Mặt phẳng \(\left( P \right):2x - 3y + 4z - 5 = 0\) nhận véc tơ \(\overrightarrow n  = \left( {2; - 3;4} \right)\) làm véc tơ pháp tuyến.

Một vectơ pháp tuyến của \(\left( P \right)\) là \(\vec{n}=\left( 1;-\,2;3 \right).\)

\(\left( P \right):\,\,2x-5z+1=0\) có 1 VTPT là \(\overrightarrow{n}=\left( 2;0;-5 \right)\).

\(A,B,C\) lần lượt là hình chiếu của \(M\left( {1;2;3} \right)\) trên các trục \(Ox,Oy,Oz\) nên \(A\left( {1;0;0} \right),B\left( {0;2;0} \right),C\left( {0;0;3} \right)\)

Phương trình mặt phẳng \(\left( {ABC} \right)\) là \(\dfrac{x}{1} + \dfrac{y}{2} + \dfrac{z}{3} = 1 \Leftrightarrow 6x + 3y + 2z = 6 \Leftrightarrow 6x + 3y + 2z - 6 = 0\).

Bước 1: Giả sử \(A(a;0;0) \in Ox,B(0;b;0) \in Oy,C(0;0;c) \in Oz\) và \((a,b,c > 0)\). Lập phương trình mặt phẳng (P) theo a, b, c.

Giả sử \(A(a;0;0) \in Ox,B(0;b;0) \in Oy,C(0;0;c) \in Oz\) và \((a,b,c > 0)\).

Ta có \(OA + OB + OC = a + b + c\).

Phương trình mặt phẳng \((P)\) có dạng: \(\dfrac{x}{a} + \dfrac{y}{b} + \dfrac{z}{c} = 1\).

Bước 2: Tìm giá trị nhỏ nhất của a+b+c

Ta có \(M(1;4;9) \in (P) \Rightarrow \dfrac{1}{a} + \dfrac{4}{b} + \dfrac{9}{c} = 1\). Do đó

\(\left( {\dfrac{1}{a} + \dfrac{4}{b} + \dfrac{9}{c}} \right)(a + b + c)\)\( = \left( {{{\left( {\sqrt {\dfrac{1}{a}} } \right)}^2} + {{\left( {\sqrt {\dfrac{4}{b}} } \right)}^2} + {{\left( {\sqrt {\dfrac{9}{c}} } \right)}^2}} \right)\left( {{{(\sqrt a )}^2} + {{(\sqrt b )}^2} + {{(\sqrt c )}^2}} \right)\)\( \ge {(1 + 2 + 3)^2}\)

\( \Rightarrow a + b + c \ge {(1 + 2 + 3)^2}\)

Dấu "=" xảy ra khi và chỉ khi

\(\left\{ {\begin{array}{*{20}{l}}{\dfrac{1}{a} + \dfrac{4}{b} + \dfrac{9}{c} = 1}\\{\dfrac{1}{a} = \dfrac{2}{b} = \dfrac{3}{c}}\\{a + b + c = {{(1 + 2 + 3)}^2}}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 6}\\{b = 12}\\{c = 18}\end{array}} \right.\)

Bước 3: Tìm điểm (P) đi qua.

\( \Rightarrow (P):\dfrac{x}{6} + \dfrac{y}{{12}} + \dfrac{z}{{18}} = 1\)

Vậy mặt phẳng \((P)\) đi qua điểm \((6;0;0)\).

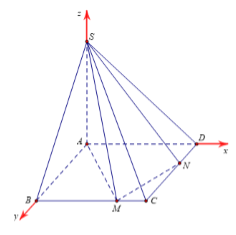
Chọn hệ trục tọa độ Axyz như hình vẽ.

Ta có: $A\left( {0;0;0} \right),{\mkern 1mu} S\left( {0;0;b} \right),{\mkern 1mu} M\left( {x;a;0} \right),{\mkern 1mu} N\left( {a;y;0} \right)$

$ \Rightarrow \overrightarrow {AM} \left( {x;a;0} \right),{\mkern 1mu} \overrightarrow {AS} \left( {0;0;b} \right)$

$ \Rightarrow $ Vtpt của $\left( {SAM} \right)$ là: $\overrightarrow {{n_1}}  = \left( {\overrightarrow {AM} ;{\mkern 1mu} \overrightarrow {AS} } \right) = \left( {ab; - bx;0} \right) = b\left( {a; - x;0} \right)$

$\overrightarrow {MS} \left( { - x; - a;b} \right),{\mkern 1mu} \overrightarrow {NS} \left( { - a; - y;b} \right)$

$ \Rightarrow $ vtpt của $\left( {SMN} \right)$ là: $\overrightarrow {{n_2}}  = \left( {\overrightarrow {MS} ;\overrightarrow {NS} } \right) = \left( {by - ab;bx - ab;xy - {a^2}} \right)$

Để hai mặt phẳng $(SAM)$ và $(SMN)$ vuông góc với nhau thì $\overrightarrow {{n_1}} .\overrightarrow {{n_2}}  = 0$

$ \Leftrightarrow a\left( {by - ab} \right) - x\left( {bx - ab} \right) + 0\left( {xy - {a^2}} \right) = 0$$ \Leftrightarrow {x^2} + {a^2} = a\left( {x + y} \right).$

Ta có: .$d\left( {O;\left( P \right)} \right) \le OM$

Dấu bằng xảy ra $ \Leftrightarrow OM \bot \left( P \right) \Rightarrow \left( P \right)$ nhận $\overrightarrow {OM}  = \left( {1;2;3} \right)$ là 1 VTPT. Do đó phương trình mặt phẳng (P) là: $1\left( {x - 1} \right) + 2\left( {y - 2} \right) + 3\left( {z - 3} \right) = 0\left( P \right):x + 2y + 3z - 14 = 0$

$ \Rightarrow A\left( {14;0;0} \right);B\left( {0;7;0} \right);C\left( {0;0;\dfrac{{14}}{3}} \right) \Rightarrow {V_{O.ABC}} = \dfrac{1}{6}OA.OB.OC = \dfrac{{686}}{9}.$

Gọi M(x;y;0) ∈ Oxy. Ta có$M{A^2} - 2M{B^2} = {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + 1 - 2{\left( {x - 2} \right)^2} - 2{\left( {y + 1} \right)^2} - 2.9$

Thử lần lượt 4 đáp án thì ta thấy với M(3;–4;0) thì $M{A^2} - 2M{B^2} = 3$ là lớn nhất

$M\left( {a;b;c} \right) \in \left( {Oxy} \right) \Rightarrow c = 0 \Rightarrow M\left( {a;b;0} \right)$

\(\begin{array}{*{20}{l}}{ \Rightarrow 3M{A^2} + 2M{B^2} = 3\left[ {{{\left( {a - 1} \right)}^2} + {b^2} + 9} \right] + 2\left[ {{{\left( {a - 11} \right)}^2} + {{\left( {b + 5} \right)}^2} + {{12}^2}} \right]}\\{ = 3\left( {{a^2} - 2a + {b^2} + 10} \right) + 2\left( {{a^2} - 22a + {b^2} + 10b + 290} \right)}\\{ = 3{a^2} - 6a + 3{b^2} + 30 + 2{a^2} - 44a + 2{b^2} + 20b + 580}\\{ = 5{a^2} - 50a + 5{b^2} + 20b + 610}\\{ = 5\left( {{a^2} - 10a + {b^2} + 4b + 122} \right)}\\{ = 5\left[ {{{\left( {a - 5} \right)}^2} + {{\left( {b + 2} \right)}^2} + 93} \right] \ge 465}\end{array}\)

Dấu bằng xảy ra $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 5}\\{b = {\rm{\;}} - 2}\end{array}} \right. \Rightarrow P = a + b + c = 5 - 2 + 0 = 3$

Bước 1:

Mặt phẳng \(\left( P \right)\) song song với mặt phẳng \(\left( Q \right):x + 2y - 3z + 2 = 0\) nên phương trình mặt phẳng \(\left( P \right)\) có dạng \(x + 2y - 3z + a = 0\,\,\left( {a \ne 2} \right)\)

Bước 2:

Vì \(A\left( {2; - 1;3} \right) \in \left( P \right)\) \( \Rightarrow 2 + 2.\left( { - 1} \right) - 3.3 + a = 0 \Leftrightarrow a = 9\).

Vậy phương trình mặt phẳng \(\left( P \right)\) cần tìm là: \(x + 2y - 3z + 9 = 0\).

Mặt phẳng trung trực \(\left( \alpha  \right)\)  của đoạn thẳng \(AB\) nhận \(\overrightarrow {AB} \) làm một VTPT.

Ta có: \(\overrightarrow {AB}  = \left( {2;\,\,4;\,\, - 2} \right) = 2\left( {1;\,2; - 1} \right)//\,\,\left( {1;\,\,2; - 1} \right)\)

\( \Rightarrow \left( \alpha  \right)\) nhận vecto \(\left( {1;\,2; - 1} \right)\) làm 1 VTPT.

Ta có : \(A\left( {1;3;2} \right),B\left( {2;4;\dfrac{1}{2}} \right)\) \( \Rightarrow I\left( {\dfrac{3}{2};\dfrac{7}{2};\dfrac{5}{4}} \right)\) là trung điểm của \(AB\).

\(\overrightarrow {AB}  = \left( {1;1; - \dfrac{3}{2}} \right)\) nên mặt phẳng trung trực của \(AB\) có phương trình :

\(1\left( {x - \dfrac{3}{2}} \right) + 1\left( {y - \dfrac{7}{2}} \right) - \dfrac{3}{2}\left( {z - \dfrac{5}{4}} \right) = 0\) \( \Leftrightarrow 8x + 8y - 12z - 25 = 0\).

Vectơ \(\overrightarrow {{n_3}}  = \left( {1;0; - 3} \right)\) là một vectơ pháp tuyến của mặt phẳng \((P):x - 3z + 2 = 0\).

Gọi M(x ;y ; z) ta có :

\(\begin{array}{l}AM = \sqrt {{{\left( {x - 2} \right)}^2} + {{\left( {y - 1} \right)}^2} + {{\left( {z + 1} \right)}^2}} \\BM = \sqrt {{x^2} + {{\left( {y - 3} \right)}^2} + {{\left( {z - 1} \right)}^2}} \\ \Rightarrow 2A{M^2} - B{M^2} = 4\\ \Leftrightarrow 2\left[ {{{\left( {x - 2} \right)}^2} + {{\left( {y - 1} \right)}^2} + {{\left( {z + 1} \right)}^2}} \right] - \left[ {{x^2} + {{\left( {y - 3} \right)}^2} + {{\left( {z - 1} \right)}^2}} \right] = 4\\ \Leftrightarrow 2\left( {{x^2} - 4x + 4 + {y^2} - 2y + 1 + {z^2} + 2z + 1} \right)\\\,\,\, - \left( {{x^2} + {y^2} - 6y + 9 + {z^2} - 2z + 1} \right) = 4\\ \Leftrightarrow {x^2} + {y^2} + {z^2} - 8x + 2y + 6z - 2 = 0\\ \Rightarrow M \in \left( S \right):{x^2} + {y^2} + {z^2} - 8x + 2y + 6z - 2 = 0\end{array}\)

Mà \(M \in \left( \alpha  \right):x + y + z + 3 = 0\) nên M thuộc đường tròn giao tuyến của mặt cầu (S) với mặt phẳng \(\left( \alpha  \right)\)

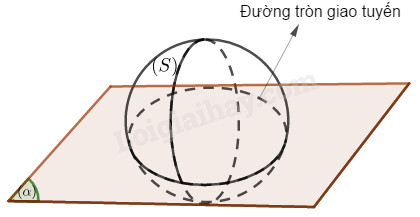
(S) có tâm I(4 ;-1 ;-3) bán kính \(R = \sqrt {{4^2} + {{\left( { - 1} \right)}^2} + {{\left( { - 3} \right)}^2} + 2}  = \sqrt {28} \)

\(\begin{array}{l}d = d\left( {I,\left( \alpha  \right)} \right) = \dfrac{{\left| {4 - 1 - 3 + 3} \right|}}{{\sqrt {{1^2} + {1^2} + {1^2}} }} = \sqrt 3 \\ \Rightarrow r = \sqrt {{R^2} - {d^2}}  = \sqrt {28 - 3}  = 5\end{array}\)

Ta có : \(\overrightarrow {BC}  = \left( {1; - 2; - 5} \right)\).

Mặt phẳng đi qua \(A\) và vuông góc với \(BC\) nên nhận \(\overrightarrow {BC} \) làm VTPT.

Vậy phương trình mặt phẳng là: \(1\left( {x - 2} \right) - 2\left( {y - 1} \right) - 5\left( {z + 1} \right) = 0\)\( \Leftrightarrow x - 2y - 5z - 5 = 0\).

Ta có: \(\overrightarrow {BC}  = \left( { - 4;4; - 2} \right)\) là 1 VTPT của mặt phẳng qua A và vuông góc với đường thẳng BC.

Mặt phẳng đi qua A và vuông góc với đường thẳng BC nhận \(\overrightarrow {BC}  = \left( { - 4;4; - 2} \right)\) là VTPT, có phương trình là:

\( - 4\left( {x - 1} \right) + 4\left( {y - 1} \right) - 2\left( {z + 2} \right) = 0\)\( \Leftrightarrow  - 4x + 4y - 2z - 4 = 0\) \( \Leftrightarrow 2x - 2y + z + 2 = 0\)

Ta có phương trình mặt phẳng đi qua ba điểm \(A\left( {2;\,0;\,0} \right)\), \(B\left( {0; - 1;\,\,0} \right)\) và \(C\left( {0;\,\,0;\,\,3} \right)\) là: \(\dfrac{x}{2} + \dfrac{y}{{ - 1}} + \dfrac{z}{3} = 1.\)

Gọi vecto pháp tuyến của mặt phẳng \(\left( Q \right)\) là \(\overrightarrow u \)

Ta có mặt phẳng \(\left( Q \right)\) đi qua \(A\left( {2;4;1} \right);B\left( { - 1;1;3} \right)\) và vuông góc với mặt phẳng \(\left( P \right)\):\(x - 3y + 2z - 5 = 0\)

Nên \(\left\{ \begin{array}{l}\overrightarrow u  \bot \overrightarrow {AB}  = \left( { - 3; - 3;2} \right)\\\overrightarrow u  \bot \overrightarrow n  = \left( {1; - 3;2} \right)\end{array} \right.\)\( \Rightarrow \overrightarrow u  = \left[ {\overrightarrow {AB} ;\overrightarrow n } \right] = \left( {0;8;12} \right)\) hay \(\left( {0;2;3} \right)\)

Mặt phẳng \(\left( Q \right)\) có vecto pháp tuyến \(\overrightarrow u  = \left( {0;2;3} \right)\) và đi qua điểm \(A\left( {2;4;1} \right)\) nên có phương trình là \(2y + 3z - 11 = 0\).

Cách dùng MTCT tìm tích có hướng:

Bước 1: Ấn SHIFT + 8 + 1 + 1 thì được màn hình:

Bước 2: Điền vecto $\overrightarrow {AB}$

Bước 3: SHIFT + 5 + 2 + 2, điền vecto \(\overrightarrow n \) vào thì được màn hình

Bước 4: Ấn AC => Ấn "SHIFT 3" + "SHIFT 4" rồi ấn dấu "=" thì được tích có hướng:

\(A\left( { - 3;0;0} \right),\,B\left( {0;0;3} \right),C\left( {0; - 3;0} \right)\)

+) Xác định điểm \(I\) thỏa mãn \(\overrightarrow {IA}  + \overrightarrow {IB}  - \overrightarrow {IC}  = \overrightarrow 0 \):

\(\overrightarrow {IA}  + \overrightarrow {IB}  - \overrightarrow {IC}  = \overrightarrow 0  \Leftrightarrow \overrightarrow {IA}  = \overrightarrow {BC}  \Leftrightarrow \left\{ \begin{array}{l} - 3 - {x_I} = 0 - 0\\0 - {y_I} =  - 3 - 0\\0 - {z_I} = 0 - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_I} =  - 3\\{y_I} = 3\\{z_I} = 3\end{array} \right. \Rightarrow I\left( { - 3;3;3} \right)\)

+) Khi đó, \(M{A^2} + M{B^2} - M{C^2} = {\overrightarrow {MA} ^2} + {\overrightarrow {MB} ^2} - {\overrightarrow {MC} ^2} = {\left( {\overrightarrow {MI}  + \overrightarrow {IA} } \right)^2} + {\left( {\overrightarrow {MI}  + \overrightarrow {IB} } \right)^2} - {\left( {\overrightarrow {MI}  + \overrightarrow {IC} } \right)^2}\)

\( = M{I^2} + 2\overrightarrow {MI} .\left( {\overrightarrow {IA}  + \overrightarrow {IB}  - \overrightarrow {IC} } \right) + I{A^2} + I{B^2} - I{C^2} = M{I^2} + I{A^2} + I{B^2} - I{C^2}\)

\(M{A^2} + M{B^2} - M{C^2}\) nhỏ nhất khi và chỉ khi \(MI\) ngắn nhất\( \Leftrightarrow M\) là hình chiếu vuông góc của I lên \(\left( {Oxy} \right)\).

\( \Leftrightarrow M\left( { - 3;3;0} \right)\)\( \Rightarrow {a^2} + {b^2} - {c^2} = {\left( { - 3} \right)^2} + {3^2} - 0 = 18\).

Nhận thấy \((P):x - y + 3 = 0\) nhận \(\overrightarrow n  = \left( {1; - 1;0} \right)\) làm véc tơ pháp tuyến nên các véc tơ \(\overrightarrow a  = \left( {3; - 3;0} \right),\overrightarrow a  = \left( { - 1;1;0} \right)\) cũng là các véc tơ pháp tuyến của \(\left( P \right)\).