Hai vật m1=5kg,m2=10kg được nối với nhau bằng một dây nhẹ, đặt trên mặt phẳng nằm ngang không ma sát. Tác dụng nằm ngang F=18N lên vật m1.
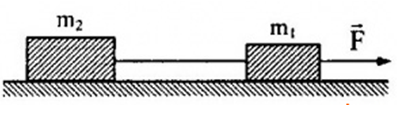
Biết dây chịu lực căng tối đa là 15N. Vậy khi hai vật chuyển động dây có lực căng là bao nhiêu và có bị đứt không?
Thay a=1,2m/s vào phương trình (b) ở câu trên, ta được: T2=10.1,2=12N
Nhận thấy: T2=T1=T=12N<Tmax=15N
=> Dây không bị đứt
Hai vật m1=5kg,m2=10kg được nối với nhau bằng một dây nhẹ, đặt trên mặt phẳng nằm ngang không ma sát. Tác dụng nằm ngang F=18N lên vật m1.

Độ lớn lực kéo bằng bao nhiêu để dây bị đứt?
Ta có:
+ Gia tốc: a=Fm1+m2 ta tính được ở câu 3
thay a vào phương trình (b), ta được: T2=T=m2Fm1+m2
+ Để dây bị đứt thì:
T≥Tmax=15N↔m2Fm1+m2≥Tmax→F≥Tmaxm1+m2m2=155+1010=22,5N
=> Để dây bị đứt thì lực kéo F≥22,5N

Vật (1) được nối với vật (2) bằng dây không dãn. m1=m2=2kg. Kéo vật m1 bằng lực 10N theo phương ngang là hệ vật chuyển động với gia tốc 2m/s2. Lấy g=10m/s2
Hệ số ma sát của mặt sàn là:
- Lực ma sát: Fms=μN=μ(m1+m2)g
Áp dụng định luật II - Niutơn cho cơ hệ, ta có:
FK−Fms=(m1+m2)a→Fms=FK−(m1+m2)a↔μ(m1+m2)g=FK−(m1+m2)a→μ=FK−(m1+m2)a(m1+m2)g=10−4.24.10=0,05

Vật (1) được nối với vật (2) bằng dây không dãn. m1=m2=2kg. Kéo vật m1 bằng lực 10N theo phương ngang là hệ vật chuyển động với gia tốc 2m/s2. Lấy g=10m/s2
Lực căng của dây có giá trị là:
Áp dụng định luật II - Niutơn cho vật thứ 2 ta được:
T−μm2g=m2a→T=μm2g+m2a=0,05.2.10+2.2=5N
Cho cơ hệ như hình vẽ
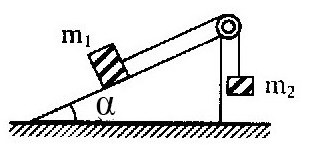
Biết m1=5kg, α=300, m2=2kg, μ=0,1. Cho g=10m/s2
Tìm gia tốc chuyển động.
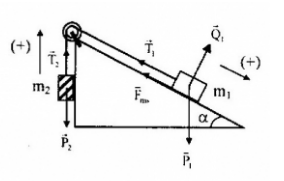
Chọn chiều dương hướng dọc theo sợi dây
Các ngoại lực tác dụng vào hệ hai vật :Trọng lực →p1, →p2 ; phản lực →Q1 của mặt phẳng nghiêng lên m1; lực ma sát giữa mặt phẳng nghiêng và vật m1 là →Fms1
-Gia tốc của hệ là: →a=→Fngmhe=→P1+→P2+→Q1+→Fms1m1+m2(1)
-Chiếu (1) lên chiều dương đã chọn, ta được:
a=psinα−p2−Fms1m1+m2=m1gsinα−m2g−μm1gcosαm1+m2
→a=g[(sinα−μcosα)m1−m2]m1+m2
=10[(sin30−0,1.cos30).5−2]5+2≈0,1m/s
Cho cơ hệ như hình vẽ

Biết m1=5kg, α=300, m2=2kg, μ=0,1. Cho g=10m/s2
Lực căng của dây có giá trị?
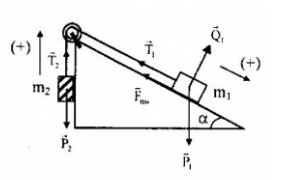
Chọn chiều dương hướng dọc theo sợi dây
Các ngoại lực tác dụng vào hệ hai vật :Trọng lực →p1, →p2 ; phản lực →Q1 của mặt phẳng nghiêng lên m1; lực ma sát giữa mặt phẳng nghiêng và vật m1 là →Fms1
-Gia tốc của hệ là: →a=→Fngmhe=→P1+→P2+→Q1+→Fms1m1+m2(1)
-Chiếu (1) lên chiều dương đã chọn, ta được:
a=psinα−p2−Fms1m1+m2=m1gsinα−m2g−μm1gcosαm1+m2
→a=g[(sinα−μcosα)m1−m2]m1+m2
=10[(sin30−0,1.cos30).5−2]5+2≈0,1m/s
- Xét riêng vật m2, ta có:
→T2+→P2=m2→a2
→T−m2g=m2a(T2=T;a1=a2=a)→T=m2(a+g)=2.(0,1+10)=20,2N
Cho cơ hệ như hình vẽ:
Biết α=300, m1=1kg;m2=2kg. Tính công của của trọng lực tác dụng lên hệ thống khi m1 đi lên không ma sát trên mặt phẳng nghiêng được quãng đường 1m
Khi m1 đi lên quãng đường s=1m trên mặt phẳng nghiêng thì m2đi xuống thẳng đứng một quãng đường cũng băng s (hình vẽ)
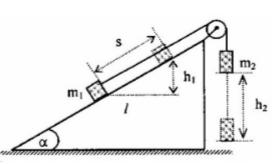
Ta có: h1=s.sinα=1.0,5=0,5m;h2=s=1m
Công của trọng lực của hệ thống:
A=A1+A2
↔A=−m1gh1+m2gh2=−1.10.0,5+2.10.1=15J
Hai vật A và B có thể trượt trên mặt bàn nằm ngang và được nối với nhau bằng dây không dãn, khối lượng không đáng kể. Khối lượng 2 vật là mA = 2kg, mB = 1kg, ta tác dụng vào vật A một lực F = 9N theo phương song song với mặt bàn. Hệ số ma sát giữa hai vật với mặt bàn là µ = 0,2. Lấy g = 10m/s2. Hãy tính gia tốc chuyển động.
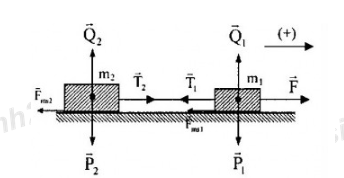
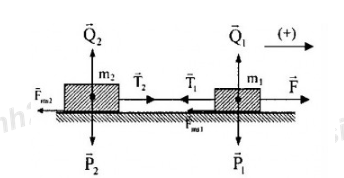
* Đối với vật A ta có: →P1+→Q1+→F+→T1+→Fms1=m1→a1
Chiếu theo phương chuyển động và phương vuông góc với phương chuyển động (chiều dương hướng lên) ta có:
{F−T1−F1ms=m1a1−m1g+Q1=0⇒{F−T1−F1ms=m1a1Q1=m1g⇒N1=Q1=m1g
Với F1ms=μN1=μm1g⇒F−T1−μm1g=m1a1(1)
* Đối với vật B: →P2+→Q2+→T2+→Fms2=m2→a2
Chiếu theo phương chuyển động và phương vuông góc với phương chuyển động (chiều dương hướng lên) ta có:
{T2−F2ms=m2a2−m2g+Q2=0⇒{T2−F2ms=m2a2Q2=m2g⇒N2=Q2=m2g
Với F2ms=μN2=μm2g⇒T2−μm2g=m2a2(2)
Vì dây không dãn nên:
{T1=T2=Ta1=a2=a⇒{F−T−μm1g=m1a(3)T−μm2g=m2a(4)
Cộng (3) và (4) ta được : F−μ(m1+m2)g=(m1+m2)a
⇒a=F−μ(m1+m2).gm1+m2=9−0,2(2+1).102+1=1m/s2

