Câu hỏi:
2 năm trước
Cho cơ hệ như hình vẽ
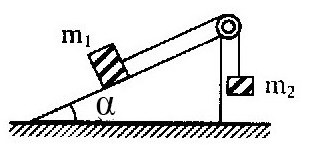
Biết \({m_1} = 5kg\), \(\alpha = {30^0}\), \({m_2} = 2kg\), \(\mu = 0,1\). Cho \(g = 10m/{s^2}\)
Tìm gia tốc chuyển động.
Trả lời bởi giáo viên
Đáp án đúng: a
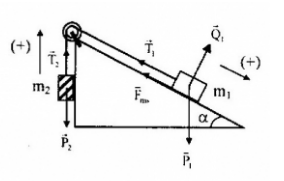
Chọn chiều dương hướng dọc theo sợi dây
Các ngoại lực tác dụng vào hệ hai vật :Trọng lực \(\overrightarrow {{p_1}} \), \(\overrightarrow {{p_2}} \) ; phản lực \(\overrightarrow {{Q_1}} \) của mặt phẳng nghiêng lên \({m_1}\); lực ma sát giữa mặt phẳng nghiêng và vật \({m_1}\) là \(\overrightarrow {{F_{m{\rm{s}}1}}} \)
-Gia tốc của hệ là: \(\overrightarrow a = \dfrac{{\overrightarrow {{F_{ng}}} }}{{{m_{he}}}} = \dfrac{{\overrightarrow {{P_1}} + \overrightarrow {{P_2}} + \overrightarrow {{Q_1}} + \overrightarrow {{F_{m{\rm{s1}}}}} }}{{{m_1} + {m_2}}}(1)\)
-Chiếu (1) lên chiều dương đã chọn, ta được:
\(a = \dfrac{{p\sin \alpha - {p_2} - {F_{m{\rm{s}}1}}}}{{{m_1} + {m_2}}} = \dfrac{{{m_1}g\sin \alpha - {m_2}g - \mu {m_1}gc{\rm{os}}\alpha }}{{{m_1} + {m_2}}}\)
\( \to a = \dfrac{{{\rm{g[(}}\sin \alpha - \mu c{\rm{os}}\alpha ){m_1} - {m_2}{\rm{]}}}}{{{m_1} + {m_2}}}\)
\( = \dfrac{{{\rm{10[(}}\sin 30 - 0,1.c{\rm{os30}}).5 - 2{\rm{]}}}}{{5 + 2}} \approx 0,1m/s\)
Hướng dẫn giải:
- Chọn chiều dương của chuyển động
- Xác định các lực tác dụng lên hệ
- Sử dụng công thức tính gia tốc của hệ: \(\overrightarrow a = \dfrac{{\overrightarrow {{F_{ng}}} }}{{{m_{he}}}}\)
- Chiếu trên chiều dương đã chọn
