Một lượng không khí nóng được chứa trong một xilanh đặt nằm ngang có pit-tông có thể dịch chuyển được. Không khí nóng dãn nở đẩy pit-tông dịch chuyển. Nếu không khí nóng thực hiện một công có độ lớn là 5000J, thì nội năng của nó biến thiên một lượng bằng bao nhiêu? Biết Xilanh cách nhiệt.
Khí thực hiện công và xi lanh cách nhiệt nên: {A=−5000JQ=0
→ Độ biến thiên nội năng: ΔU=A+Q=−5000+0=−5000J
Người ta truyền cho khí trong xi lanh nhiệt lượng 250J. Khí nở ra thực hiện công 70J đẩy pittong lên. Độ biến thiên nội năng của khí là:
Theo nguyên lí I NĐLH: ΔU=A+Q
Khí trong xilanh nhận nhiệt lượng và thực hiện công nên:
{Q>0A<0⇒{Q=250JA=−70J
Độ biến thiên nội năng của khí:
ΔU=A+Q=−70+250=180J
Người ta cung cấp nhiệt lượng 1,5J cho chất khí đựng trong một xilanh đặt nằm ngang. Chất khí nở ra, đẩy pittong đi một đoạn 5cm. Tính độ biến thiên nội năng của chất khí. Biết lực ma sát giữa pittong và xilanh có độ lớn 20N:
Công do chất khí thực hiện để thắng lực ma sát có độ lớn là: |A|=F.l=20.0,05=1J
Chất khí nhận nhiệt lượng và thực hiện công nên: {Q>0A<0⇒{Q=1,5JA=−1J
Độ biến thiên nội năng là: ΔU=A+Q=−1+1,5=0,5J
Biểu thức nào sau đây là biểu thức của nguyên lí I của nhiệt động lực học?
Nguyên lí I của nhiệt động lực học: Độ biến thiên nội năng của hệ bằng tổng công và nhiệt lượng mà hệ nhận được: ΔU=A+Q
Trường hợp nội năng của vật bị biến đổi không phải do truyền nhiệt là
A, B, C - nội năng bị biến đổi do truyền nhiệt
D - cọ xát đồng xu vào mặt bàn ta thấy đồng xu nóng lên thì nội năng bị biến đổi do thực hiện công
Phát biểu đúng với nguyên lí I nhiệt động lực học là:
A – sai vì: Độ biến thiên nội năng của hệ bằng tổng đại số nhiệt lượng và công mà hệ nhận được.
B – sai vì: Với A > 0, vật thực nhận công
C - đúng
D - sai vì Q=ΔU−A
Biểu thức diễn tả đúng quá trình chất khí vừa truyền nhiệt vừa thực hiện công là:
ΔU=A+Q
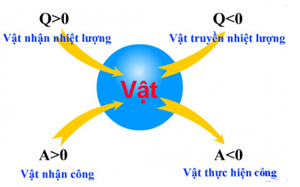
=> Chất khí vừa nhận nhiệt vừa nhận công => ΔU=Q+A;Q<0;A<0
Công A và nhiệt lượng Q cùng dấu với nhau trong trường hợp hệ:
Ta có:
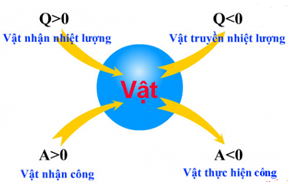
=> Công A và nhiệt lượng Q cùng dấu với nhau trong trường hợp các trường hợp:
+ Vật nhận nhiệt lượng và nhận công
+ Vật truyền nhiệt lượng và thực hiện công.
Độ biến thiên nội năng trong quá trình đẳng nhiệt có giá trị là:
Ta có, trong quá trình đẳng nhiệt
T=0→ΔU=0 nên Q=−A
Trong quá trình đẳng tích, độ biến thiên nội năng
Ta có, trong quá trình đẳng tích ΔV=0→A=0 nên ΔU=Q
Công thức mô tả đúng nguyên lí I của nhiệt động lực học là
Nguyên lí I của nhiệt động lực học: Độ biến thiên nội năng của hệ bằng tổng công và nhiệt lượng mà hệ nhận được: ΔU=A+Q
Trường hợp nội năng của vật bị biến đổi không phải do truyền nhiệt là
A, B, D - nội năng bị biến đổi do truyền nhiệt
C - ta xoa hai bàn tay vào nhau cho ấm lên thì nội năng bị biến đổi do thực hiện công
Phát biểu không đúng với nguyên lí I nhiệt động lực học là:
A, B, C - đúng
D - sai
Biểu thức diễn tả đúng quá trình chất khí vừa nhận nhiệt vừa nhận công là:
ΔU=A+Q
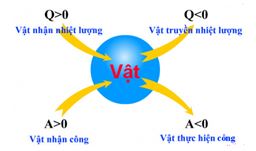
=> Chất khí vừa nhận nhiệt vừa nhận công => ΔU=Q+A;Q>0;A>0
Công A và nhiệt lượng Q trái dấu với nhau trong trường hợp hệ:
Ta có:
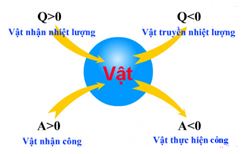
=> Công A và nhiệt lượng Q trái dấu với nhau trong trường hợp: Vật nhận nhiệt và thực hiện công hoặc vật truyền nhiệt lượng và nhận công.
ΔU=0 trong trường hợp hệ:
ΔU=0 trong trường hợp hệ biến đổi theo chu trình.
ΔU=Q là hệ thức của nguyên lí I áp dụng cho:
ΔU=Q là hệ thức của nguyên lí I áp dụng cho quá trình đẳng tích
Một viên đạn bằng chì khối lượng m, bay với vận tốc v=195m/s, va chạm mềm vào một quả cầu bằng chì cùng khối lượng m đang đứng yên. Nhiệt dung riêng của chì là c=130J/kg.K. Nhiệt độ ban đầu của viên đạn và quả cầu bằng nhau. Coi nhiệt lượng truyền ra môi trường là không đáng kể. Độ tăng nhiệt độ của viên đạn và quả cầu là:
Theo định luật bảo toàn động lượng: mv = (m + m)v’ ⇒ v’ = v/2
Độ hao hụt cơ năng:
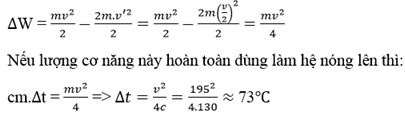
Một lượng khí lí tưởng thực hiện quá trình đẳng áp 1 – 2 rồi đẳng nhiệt 2 – 3. Trong mỗi đoạn, khí nhận công hay sinh công?
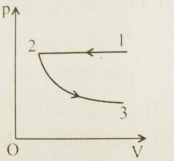
Từ đồ thị, ta có:
+ Quá trình 1→2: Quá trình đẳng áp, trong quá trình này:
- Áp suất không đổi
- Thể tích giảm V2<V1
- Lại có V1T1=V2T2⇒V1V2=T1T2>1⇒T1>T2
=> Nhiệt độ giảm
=> Vật nhận công
+ Quá trình 2→3: Quá trình đẳng nhiệt, trong quá trình này:
- Nhiệt độ không đổi
- Thể tích khí tăng nên vật thực hiện công
Một khí lí tưởng thực hiện quá trình đẳng tích 1 – 2 rồi đẳng áp 2 – 3. Trong mỗi đoạn, khí nhận nhiệt hay tỏa nhiệt?
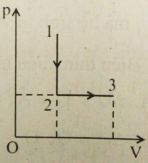
Từ đồ thị, ta có:
+ Quá trình 1→2: Quá trình đẳng tích, trong quá trình này
- Thể tích không đổi
- Lại có: p1T1=p2T2 và p1>p2
Ta suy ra T2>T1 => Nhiệt độ tăng nên nội năng tăng
=> Khí tỏa nhiệt
+ Quá trình 2→3: Quá trình đẳng áp, trong quá trình này:
- Áp suất không đổi
- Thể tích khí tăng (V3>V2)
=> Nhiệt độ khí tăng => Nội năng tăng
=> Khí sinh công => Khí nhận nhiệt

