Nguyên hàm

Trên khoảng \(\left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\) ta có:

 \(\begin{array}{l}f\left( x \right) = \int\limits_{}^{} {f'\left( x \right)dx}  = \int\limits_{}^{} {\frac{1}{{{x^2} - 1}}dx}  = \frac{1}{2}\int\limits_{}^{} {\left( {\frac{1}{{x - 1}} - \frac{1}{{x + 1}}} \right)dx}  = \frac{1}{2}\ln \left| {\frac{{x - 1}}{{x + 1}}} \right| + {C_1} = \frac{1}{2}\ln \frac{{x - 1}}{{x + 1}} + {C_1}\\f\left( { - 3} \right) + f\left( 3 \right) = \frac{1}{2}\ln 2 + \frac{1}{2}\ln \frac{1}{2} + {C_1} = 0 \Leftrightarrow {C_1} = 0\end{array}\)

Trên khoảng \(\left( { - 1;1} \right)\) ta có:

\(\begin{array}{l}f\left( x \right) = \int\limits_{}^{} {f'\left( x \right)dx}  = \int\limits_{}^{} {\frac{1}{{{x^2} - 1}}dx}  = \frac{1}{2}\ln \left| {\frac{{x - 1}}{{x + 1}}} \right| + {C_2} = \frac{1}{2}\ln \frac{{ - x + 1}}{{x + 1}} + {C_2}\\f\left( { - \frac{1}{2}} \right) + f\left( {\frac{1}{2}} \right) = \frac{1}{2}\ln 3 + \frac{1}{2}\ln \frac{1}{3} + {C_2} = 2 \Leftrightarrow {C_2} = 2\\ \Rightarrow f\left( x \right) = \left\{ \begin{array}{l}\frac{1}{2}\ln \frac{{x - 1}}{{x + 1}}\,\,khi\,\,x \in \left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\\\frac{1}{2}\ln \frac{{ - x + 1}}{{x + 1}} + 2\,\,khi\,\,x \in \left( { - 1;1} \right)\end{array} \right.\\\Rightarrow T = f\left( { - 2} \right) + f\left( 0 \right) + f\left( 5 \right) = \frac{1}{2}\ln 3 + \frac{1}{2}\ln 1 + 2 + \frac{1}{2}\ln \frac{2}{3} = \ln \sqrt 2  + 2\end{array}\)

Ta có \(f\left( x \right) = \left| {1 + x} \right| - \left| {1 - x} \right| = \left\{ \begin{array}{l}
2\,\,\,\,\,\,\,\,\,\,khi\,\,\,\,x \ge 1\\
2x\,\,\,\,\,\,\,\,khi\,\,\,\, - \,1 \le x < 1\\
- \,2\,\,\,\,\,\,\,khi\,\,\,\,\,x < - \,1
\end{array} \right. \Rightarrow F\left( x \right) = \left\{ \begin{array}{l}
2x + {C_1}\,\,\,\,\,\,\,\,khi\,\,\,\,x \ge 1\\
{x^2} + {C_2}\,\,\,\,\,\,\,\,khi\,\,\,\, - \,1 \le x < 1\\
- \,2x + {C_3}\,\,\,\,khi\,\,\,\,\,x < - \,1
\end{array} \right.\)

Theo đề bài ta có \(\left\{ \begin{array}{l}
F\left( 1 \right) = 3\\
F\left( { - 1} \right) = 2\\
F\left( { - 2} \right) = 4
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
2 + {C_1} = 3\\
1 + {C_2} = 2\\
4 + {C_3} = 4
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{C_1} = 1\\
{C_2} = 1\\
{C_3} = 0
\end{array} \right.\)

\(\begin{array}{l}
\Rightarrow F\left( x \right) = \left\{ \begin{array}{l}
2x + 1\,\,\,\,\,\,\,\,khi\,\,\,\,x \ge 1\\
{x^2} + 1\,\,\,\,\,\,\,\,khi\,\,\,\, - \,1 \le x < 1\\
- \,2x\,\,\,\,khi\,\,\,\,\,x < - \,1
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
F\left( 2 \right) = 2.2 + 1 = 5\\
F\left( 0 \right) = 1\\
F\left( { - 3} \right) = - 2.\left( { - 3} \right) = 6.
\end{array} \right.\\
\Rightarrow T = 5 + 1 + 6 = 12.
\end{array}\)

\(\begin{array}{l}f'(x) = \frac{1}{{{x^2} - 1}} \Rightarrow \int {f'(x)dx}  = \int {\frac{1}{{{x^2} - 1}}dx}  \Rightarrow f(x) = \int {\frac{1}{{(x - 1)(x + 1)}}dx}  = \frac{1}{2}\int {\frac{1}{{x - 1}}dx + } \frac{1}{2}\int {\frac{1}{{x + 1}}dx = \frac{1}{2}\ln \left| {\frac{{x - 1}}{{x + 1}}} \right| + C} \\ \Rightarrow f(x) = \left\{ \begin{array}{l}\frac{1}{2}\ln \left| {\frac{{x - 1}}{{x + 1}}} \right| + {C_1},\left[ \begin{array}{l}x <  - 1\\x > 1\end{array} \right.\\\frac{1}{2}\ln \left| {\frac{{x - 1}}{{x + 1}}} \right| + {C_2}, - 1 < x < 1\end{array} \right.\end{array}\)

Ta có:

\(f(-3)+f(3)=0\Leftrightarrow \frac{1}{2}\ln 2+{{C}_{1}}+\frac{1}{2}\ln \frac{1}{2}+{{C}_{1}}=0\Leftrightarrow 2{{C}_{1}}=0\Leftrightarrow {{C}_{1}}=0\)

\(f\left( -\frac{1}{2} \right)+f\left( \frac{1}{2} \right)=2\Leftrightarrow \frac{1}{2}\ln 3+{{C}_{2}}+\frac{1}{2}\ln \frac{1}{3}+{{C}_{2}}=2\Leftrightarrow {{C}_{2}}=1\)

\(P=f(0)+f(4)=\left( \frac{1}{2}\ln \left| \frac{0-1}{0+1} \right|+1 \right)+\left( \frac{1}{2}\ln \left| \frac{4-1}{4+1} \right| \right)=\frac{1}{2}\ln \frac{3}{5}+1\)

Ta có \(f\left( x \right)=\int{{f}'\left( x \right)\,\text{d}x}=\int{\frac{\text{d}x}{{{x}^{2}}-1}}=\frac{1}{2}\ln \left| \frac{x-1}{x+1} \right|+C=\left\{ \begin{align} & \frac{1}{2}\ln \frac{x-1}{x+1}+{{C}_{1}}\,\,\,\,\,khi\,\,\,x>1 \\ & \frac{1}{2}\ln \frac{1-x}{x+1}+{{C}_{2}}\,\,\,\,\,khi\,\,\,-\,1<x<1 \\ & \frac{1}{2}\ln \frac{x-1}{x+1}+{{C}_{3}}\,\,\,\,\,khi\,\,\,x<-\,1 \\ \end{align} \right..\)

Suy ra \(f\left( -\,3 \right)+f\left( 3 \right)=0\Leftrightarrow \,\,\frac{1}{2}\ln 2+{{C}_{1}}+\frac{1}{2}\ln \frac{1}{2}+{{C}_{3}}=0\Leftrightarrow \,\,{{C}_{1}}+{{C}_{3}}=0.\) Và \(f\left( -\frac{1}{2} \right)+f\left( \frac{1}{2} \right)=2\Leftrightarrow \,\,\frac{1}{2}\ln 3+{{C}_{2}}+\frac{1}{2}\ln \frac{1}{3}+{{C}_{2}}=2\Leftrightarrow \,\,{{C}_{2}}=1.\)

Vậy \(T=f\left( -\,2 \right)+f\left( 0 \right)+f\left( 5 \right)=\frac{1}{2}\ln 3+{{C}_{3}}+{{C}_{2}}+\frac{1}{2}\ln \frac{2}{3}+{{C}_{1}}=\frac{1}{2}\ln 2+1.\)

\(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\) nên ta có \(F'\left( x \right) = f\left( x \right)\)

Ta có:

\(\begin{array}{l}F'\left( x \right) = \left( {3a{x^2} + 2bx + c} \right){e^x} + \left( {a{x^3} + b{x^2} + cx + d} \right){e^x}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {a{x^3} + \left( {3a + b} \right){x^2} + \left( {2b + c} \right)x + c + d} \right){e^x}\end{array}\)

Do đó \(\left( {a{x^3} + \left( {3a + b} \right){x^2} + \left( {2b + c} \right)x + c + d} \right){e^x} = \left( {2{x^3} + 9{x^2} - 2x + 5} \right){e^x}\)

Đồng nhất hệ số ta có: \(\left\{ \begin{array}{l}a = 2\\3a + b = 9\\2b + c =  - 2\\c + d = 5\end{array} \right.\left\{ \begin{array}{l}a = 2\\b = 3\\c =  - 8\\d = 13\end{array} \right. \Rightarrow {a^2} + {b^2} + {c^2} + {d^2} = 246\)

Ta có  \(\left[ f\left( x \right).f'\left( x \right) \right]'={{\left[ f'\left( x \right) \right]}^{2}}+f\left( x \right).f''\left( x \right)=15{{x}^{4}}+12x\)

Nguyên hàm 2 vế ta được \(f\left( x \right).f'\left( x \right)=3{{x}^{5}}+6{{x}^{2}}+C\)

Do \(f\left( 0 \right)=f'\left( 0 \right)=1\Rightarrow C=1\)

Tiếp tục nguyên hàm 2 vế ta được: \(\int{f\left( x \right)df\left( x \right)}=\int{\left( 3{{x}^{5}}+6{{x}^{2}}+1 \right)dx}\)

\(\Rightarrow \frac{{{f}^{2}}\left( x \right)}{2}=\frac{3{{x}^{6}}}{6}+\frac{6{{x}^{3}}}{3}+x+D=\frac{1}{2}{{x}^{6}}+2{{x}^{3}}+x+D\)

Do \(f\left( 0 \right)=1\Rightarrow D=\frac{1}{2}\Rightarrow \frac{{{f}^{2}}\left( x \right)}{2}=\frac{1}{2}{{x}^{6}}+2{{x}^{3}}+x+\frac{1}{2}\Rightarrow {{f}^{2}}\left( 1 \right)=8\)

\(f'(x)\sqrt{{{x}^{2}}+1}=2x\sqrt{f(x)+1}\Leftrightarrow \frac{f'(x)}{\sqrt{f(x)+1}}=\frac{2x}{\sqrt{{{x}^{2}}+1}}\Rightarrow \int{\frac{f'(x)}{\sqrt{f(x)+1}}}dx=\int{\frac{2x}{\sqrt{{{x}^{2}}+1}}}dx\Leftrightarrow \int{\frac{d\left( f(x)+1 \right)}{\sqrt{f(x)+1}}}=\int{\frac{d({{x}^{2}}+1)}{\sqrt{{{x}^{2}}+1}}}\)

\(\Leftrightarrow 2\sqrt{f(x)+1}=2\sqrt{{{x}^{2}}+1}+C\)

Mà \(f(0)=0\Rightarrow 2\sqrt{0+1}=2\sqrt{{{0}^{2}}+1}+C\Rightarrow C=0\)

\(\Rightarrow \sqrt{f(x)+1}=\sqrt{{{x}^{2}}+1}\Leftrightarrow f(x)={{x}^{2}}\)

\(\Rightarrow f\left( \sqrt{3} \right)={{\left( \sqrt{3} \right)}^{2}}=3\)

\(f\left( x \right) = f'\left( x \right)\sqrt {3x + 1}  \Leftrightarrow \frac{{f'\left( x \right)}}{{f\left( x \right)}} = \frac{1}{{\sqrt {3x + 1} }}\)

Lấy nguyên hàm hai vế ta có \(\int\limits_{}^{} {\frac{{f'\left( x \right)}}{{f\left( x \right)}}dx}  = \int\limits_{}^{} {\frac{{dx}}{{\sqrt {3x + 1} }} \Leftrightarrow \ln \left| {f\left( x \right)} \right|}  = \frac{2}{3}\sqrt {3x + 1}  + C = \ln f\left( x \right)\,\,\,\left( {f\left( x \right) > 0} \right)\)

\(\begin{array}{l} \Rightarrow \ln \left| {f\left( 1 \right)} \right| = \frac{2}{3}.\sqrt 4  + C \Leftrightarrow C =  - \frac{4}{3} \Rightarrow \ln f\left( x \right) = \frac{2}{3}\sqrt {3x + 1}  - \frac{4}{3} \Leftrightarrow f\left( x \right) = {e^{\frac{2}{3}\sqrt {3x + 1}  - \frac{4}{3}}}\\ \Rightarrow f\left( 5 \right) = {e^{\frac{4}{3}}} \approx 3,79\end{array}\)

Chuyển vế và nhân cả hai vế với \({e^{ - x}}\) ta có:

\(\begin{array}{l}f'\left( x \right) = f\left( x \right) + {x^2}{e^x} + 1\,\,\forall x \in R\\ \Leftrightarrow f'\left( x \right){e^{ - x}} - {e^{ - x}}f\left( x \right) = {x^2} + {e^{ - x}}\end{array}\)

Ta có \(\left[ {f\left( x \right){e^{ - x}}} \right]' = f'\left( x \right){e^{ - x}} - {e^{ - x}}f\left( x \right)\)

\( \Rightarrow \left[ {f\left( x \right){e^{ - x}}} \right]' = {x^2} + {e^{ - x}}\)

Lấy nguyên hàm hai vế ta được \(f\left( x \right){e^{ - x}} = \frac{{{x^3}}}{3} - {e^{ - x}} + C \Rightarrow f\left( x \right) = \frac{{{x^3}{e^x}}}{3} - 1 + C{e^x}\)

Ta có \(f\left( 0 \right) =  - 1 \Leftrightarrow  - 1 + C =  - 1 \Leftrightarrow C = 0 \Rightarrow f\left( x \right) = \frac{{{x^3}{e^x}}}{3} - 1\)

\( \Rightarrow f\left( 3 \right) = \frac{{{3^3}.{e^3}}}{3} - 1 = 9{e^3} - 1\)

Ta có: \(\int {\left( {{e^x} + 1} \right)dx = {e^x} + x + C} \)

\(\int {f\left( x \right)dx}  = \int {\left( {3{x^2} + \sin x} \right)dx}  = {x^3} - \cos x + C\)

\(\int {\left( {3{x^2} + \dfrac{1}{{{{\cos }^2}x}}} \right)} dx = {x^3} + \tan x + C\).

Ta có: \(\int {{x^5}dx}  = \dfrac{{{x^6}}}{6} + C.\)

Ta có \(f\left( x \right) = \int {f'\left( x \right) = \int {\frac{2}{{2x - 1}}dx} } \)

\( \Rightarrow f\left( x \right) = \ln \left| {2x - 1} \right| + C\)

+) \(f\left( x \right) = \ln \left( {2x - 1} \right) + C\)\(\left( {x \ge \frac{1}{2}} \right)\)

Mà \(f\left( 1 \right) = 2 \Rightarrow f\left( x \right) = \ln \left( {2x - 1} \right) + 2\)

\( + )f\left( x \right) = \ln \left( {1 - 2x} \right) + C\)\(\left( {x < \frac{1}{2}} \right)\)

Mà \(f\left( 0 \right) = 1 \Rightarrow f\left( x \right) = \ln \left( {1 - 2x} \right) + 1\)

Với \(x =  - 1 \Rightarrow f\left( { - 1} \right) = \ln \left( {1 - 2x} \right) + 1 = \ln 3 + 1\)

Với \(x = 3 \Rightarrow f\left( 3 \right) = \ln \left( {2x - 1} \right) + 2 = \ln 5 + 2\)

\( \Rightarrow f\left( { - 1} \right) + f\left( 3 \right) = \ln 15 + 3\)

Lấy nguyên hàm hai vế biểu thức \(\dfrac{{f'\left( x \right)}}{{f\left( x \right)}} = 2 - 2x\) ta có:

\(\begin{array}{l}\int {\dfrac{{f'\left( x \right)}}{{f\left( x \right)}}dx}  = \int {\left( {2 - 2x} \right)dx} \\ \Leftrightarrow \ln \left| {f\left( x \right)} \right| =  - {x^2} + 2x + C\end{array}\)

Theo bài ra ta có \(f\left( 0 \right) = 1\) \( \Leftrightarrow \ln \left| {f\left( 0 \right)} \right| = C \Leftrightarrow \ln 1 = C \Leftrightarrow C = 0\).

\(\begin{array}{l} \Leftrightarrow \ln \left| {f\left( x \right)} \right| =  - {x^2} + 2x\\ \Leftrightarrow \left| {f\left( x \right)} \right| = {e^{ - {x^2} + 2x}}\\ \Leftrightarrow f\left( x \right) = {e^{ - {x^2} + 2x}}\,\,\left( {Do\,\,f\left( x \right) > 0\,\,\forall x \in \mathbb{R}} \right)\end{array}\)

Ta có : \(f'\left( x \right) = \left( { - 2x + 2} \right){e^{ - {x^2} + 2x}} = 0 \Leftrightarrow x = 1\).

BBT:

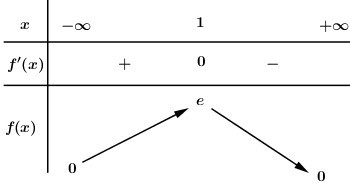
Phương trình \(f\left( x \right) = m\) có hai nghiệm thực phân biệt khi và chỉ khi đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại hai điểm phân biệt, dựa vào BBT ta suy ra \(0 < m < e\).

Ta có \(\int {f\left( x \right)dx}  = \int {\cos 5xdx}  = \dfrac{1}{5}\sin 5x + C.\)

\(\int {f\left( x \right)dx}  = \int {\sin 2xdx}  =  - \dfrac{1}{2}\cos 2x + C\).

Ta có: \(F\left( x \right) = \int {\sin 2xdx}  =  - \frac{1}{2}\cos 2x + C\) \( \Rightarrow \) đáp án C đúng.

Lại có: \( - \frac{1}{2}\cos 2x + C =  - \frac{1}{2}\left( {2{{\cos }^2}x - 1} \right) + C\)\( =  - {\cos ^2}x + C'\)\( \Rightarrow \) đáp án A đúng.

\( - \frac{1}{2}\cos 2x + C =  - \frac{1}{2}\left( {1 - 2{{\sin }^2}x} \right) + C\)\( = {\sin ^2}x + C'\) \( \Rightarrow \) đáp án B đúng.

Ta có

\(\begin{array}{l}f\left( x \right) = 3{x^2} + 8\sin x\\ \Rightarrow \int {f\left( x \right)dx = \int {3{x^2}dx + \int {8\sin xdx} } } \\ \Rightarrow \int {f\left( x \right)dx}  = {x^3} - 8\cos x + C.\end{array}\)

Ta có: \(\int {\dfrac{{dx}}{x}}  = \ln \left| x \right| + C = \ln x + C\,\,\left( {do\,\,x > 0} \right)\).

Dựa vào các đáp án ta thấy:

Đáp án A: \(\dfrac{1}{2}\ln {x^2} = \ln \left| x \right| = \ln x\) là 1 nguyên hàm của hàm số \(f\left( x \right) = \dfrac{1}{x}\) khi \(C = 0\).

Đáp án B: \(\ln x\) là một nguyên hàm của hàm số \(f\left( x \right) = \dfrac{1}{x}\) khi \(C = 0\).

Đáp án C: \(\ln 2x = \ln 2 + \ln x\) là một nguyên hàm của hàm số \(f\left( x \right) = \dfrac{1}{x}\) khi \(C = \ln 2\).