Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và thỏa mãn \(f\left( x \right) > 0,\)\(\forall x \in \mathbb{R}.\) Cho biết \(f\left( 0 \right) = 1\) và \(\dfrac{{f'\left( x \right)}}{{f\left( x \right)}} = 2 - 2x.\) Tất cả các giá trị thực của tham số \(m\) để phương trình \(f\left( x \right) = m\) có hai nghiệm thực phân biệt là:

Lấy nguyên hàm hai vế biểu thức \(\dfrac{{f'\left( x \right)}}{{f\left( x \right)}} = 2 - 2x\) ta có:

\(\begin{array}{l}\int {\dfrac{{f'\left( x \right)}}{{f\left( x \right)}}dx}  = \int {\left( {2 - 2x} \right)dx} \\ \Leftrightarrow \ln \left| {f\left( x \right)} \right| =  - {x^2} + 2x + C\end{array}\)

Theo bài ra ta có \(f\left( 0 \right) = 1\) \( \Leftrightarrow \ln \left| {f\left( 0 \right)} \right| = C \Leftrightarrow \ln 1 = C \Leftrightarrow C = 0\).

\(\begin{array}{l} \Leftrightarrow \ln \left| {f\left( x \right)} \right| =  - {x^2} + 2x\\ \Leftrightarrow \left| {f\left( x \right)} \right| = {e^{ - {x^2} + 2x}}\\ \Leftrightarrow f\left( x \right) = {e^{ - {x^2} + 2x}}\,\,\left( {Do\,\,f\left( x \right) > 0\,\,\forall x \in \mathbb{R}} \right)\end{array}\)

Ta có : \(f'\left( x \right) = \left( { - 2x + 2} \right){e^{ - {x^2} + 2x}} = 0 \Leftrightarrow x = 1\).

BBT:

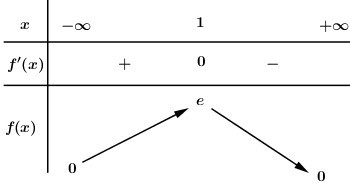
Phương trình \(f\left( x \right) = m\) có hai nghiệm thực phân biệt khi và chỉ khi đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại hai điểm phân biệt, dựa vào BBT ta suy ra \(0 < m < e\).