Lực đàn hồi

Trong giới hạn đàn hồi, độ lớn của lực đàn hồi của lò xo tỉ lệ thuận với độ biến dạng.

+ Áp dụng định luật Húc ta có:

\(F = k.\left| {\Delta l} \right| \Leftrightarrow \left| {\Delta l} \right| = \dfrac{F}{k} = \dfrac{3}{{200}} = 0,015m = 1,5cm\)

+ Chiều dài của lò xo lúc này:

\(l = {l_0} - \Delta l = 21 - 1,5 = 19,5cm\)

Theo định luật Húc ta có: \(\dfrac{{{F_{dh1}}}}{{{F_{dh2}}}} = \dfrac{{\Delta {l_1}}}{{\Delta {l_2}}}\)

Khi \(\left\{ \begin{array}{l}{F_{dh1}} = 5N \Rightarrow \Delta {l_1} = \left| {{l_1} - {l_0}} \right| = \left| {24 - 30} \right| = 6cm\\{F_{dh2}} = 10N \Rightarrow \Delta {l_2} = \left| {{l_2} - {l_0}} \right|\end{array} \right.\)

\(\begin{array}{l}\dfrac{{{F_{dh1}}}}{{{F_{dh2}}}} = \dfrac{{\Delta {l_1}}}{{\Delta {l_2}}} \Rightarrow \Delta {l_2} = \dfrac{{{F_{dh2}}.\Delta {l_1}}}{{{F_{dh1}}}} = \dfrac{{10.6}}{5} = 12cm\\ \Rightarrow {l_2} = {l_0} + \Delta {l_2} = 30 + 12 = 42cm\end{array}\)

A, B, C - đúng

D - sai vì mỗi vật có một giới hạn đàn hồi nhất định, khi lực tác dụng vượt quá giới hạn đàn hồi thì vật đó không lấy lại được hình dạng ban đầu khi thôi tác dụng

Trong giới hạn đàn hồi, lực đàn hồi của lò xo tỉ lệ thuận với độ biến dạng của lò xo

$F = k\left| {\Delta l} \right|$

A, B, C - đúng

D - sai vì: Lực đàn hồi tỉ lệ thuận với độ biến dạng của vật biến dạng

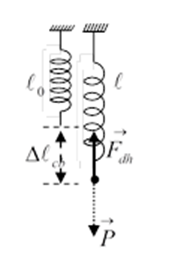
Khi cân bằng:

\(\begin{array}{l}\overrightarrow P  + \overrightarrow {{F_{dh}}}  = \overrightarrow 0 \\ \to {F_{dh}} = P\\ \leftrightarrow k\Delta l = mg\\ \to \Delta l = \frac{{mg}}{k}\end{array}\)

A, C, D - đúng

B - sai vì lực đàn hồi có khi là lực kéo, lực nén

Định luật Húc: Trong giới hạn đàn hồi, lực đàn hồi của lò xo tỉ lệ thuận với độ biến dạng của lò xo

$F = k\left| {\Delta l} \right|$

Lực đẩy của lò xo dưới yên xe đạp là lực đàn hồi

Lực mà lò xo bút bi tác dụng vào ruột bút bi là lực đàn hồi

Số chỉ trên mỗi lực kế: \(\frac{{100}}{2} = 50N\)

Ta có, tại vị trí cân bằng, lực đàn hồi của lò xo cân bằng với trọng lực của vật:

\(\begin{array}{l}{F_{dh}} = P \leftrightarrow k\left| {\Delta l} \right| = mg\\ \to k = \frac{{mg}}{{\Delta l}} = \frac{{0,2.10}}{{\left( {20 - 18} \right).{{10}^{ - 2}}}} = 100N/m\end{array}\)

Ta có:

Khi treo thêm vật  thì lò xo có độ biến dạng thêm:

\(\begin{array}{l} \to \Delta P = k\left| {\Delta l'} \right|\\ \to k = \frac{{\Delta P}}{{\left| {\Delta l'} \right|}} = \frac{1}{{0,02}} = 50N/m\end{array}\)

Ban đầu, ta có: \(\left| {\Delta l} \right| = \frac{{mg}}{k} = \frac{{0,2.10}}{{50}} = 0,04m = 4cm\)

=> Chiều dài tự nhiên của lò xo là: \(34cm - 4cm = 30cm\)

Ta có:

k - không đổi

\(\left\{ \begin{array}{l}{m_1} = 0,8kg,{l_1} = 0,24m\\{m_2} = 0,6kg,{l_2} = 0,23m\\{m_3} = 1,5kg,{l_3} = ?\end{array} \right.\)

Khi cân bằng, ta có lực đàn hồi cân bằng với trọng lực, ta có:

\(\left\{ \begin{array}{l}k\left( {{l_1} - {l_0}} \right) = {m_1}g{\rm{          }}\left( 1 \right)\\k\left( {{l_2} - {l_0}} \right) = {m_2}g{\rm{         }}\left( 2 \right)\\k\left( {{l_3} - {l_0}} \right) = {m_3}g{\rm{          }}\left( 3 \right)\end{array} \right.\)

Từ \(\left( 1 \right),\left( 2 \right)\) ta suy ra: \({l_0} = 0,2m\) thế vào \(\left( 1 \right) \to k = 200N/m\)

Thế vào \(\left( 3 \right)\), ta suy ra: \({l_3} = 0,275m = 27,5cm\)

- Khi cân bằng, ta có lực đàn hồi cân bằng với trọng lực, ta có:

\(\begin{array}{l}k\left( {{l_1} - {l_0}} \right) = {m_1}g\\ \to k = \frac{{{m_1}g}}{{{l_1} - {l_0}}} = \frac{{0,5.9,8}}{{\left( {7 - 5} \right){{.10}^{ - 2}}}} = 245N/m\end{array}\)

- Để lò xo có chiều dài \(6,5cm\) cần treo vật có khối lượng \({m_2}\) sao cho:

\(\begin{array}{l}k\left( {{l_2} - {l_0}} \right) = {m_2}g\\ \to {m_2} = \frac{{k\left( {{l_2} - {l_0}} \right)}}{g} = \frac{{245.\left( {6,5 - 5} \right){{.10}^{ - 2}}}}{{9,8}} = 0,375kg\end{array}\)

Khi có giá đỡ: \({\overrightarrow F _{đh}} + \overrightarrow P  + \overrightarrow N  = m\overrightarrow a \)

Khi giá đỡ đứng yên: Lò xo dãn một đoạn $1 cm$

Khi rời giá đỡ: \({\overrightarrow F _{đh}} + \overrightarrow P  = m\overrightarrow a  \Rightarrow P - {F_{đh}} = ma \Rightarrow mg - k\Delta {l_2} = ma \Rightarrow \Delta {l_2} = \frac{{m\left( {g - a} \right)}}{k} = \frac{{1\left( {10 - 1} \right)}}{{100}} = 0,09m = 9cm\)

Khi rời giá đỡ, lò xo giãn $9 cm$

=> Quãng đường giá đỡ đi được là $s = 8cm$

Vận tốc của vật khi rời giá đỡ là: \(v = \sqrt {2as}  = 40\,cm/s\)

Khi vật cân bằng: \({F_{dh}} = {F_K}\)

\(\begin{array}{l}
\leftrightarrow K|\Delta l| = {F_K}\\
\leftrightarrow K.0,08 = 5\\
\to K = 62,5N/m
\end{array}\)

 Đáp án C

Khi nén 1 lực 1N vào lò xo ta có \(F = k\Delta l =  > \Delta l = \frac{F}{k} = \frac{1}{{40}} = 0,025m = 2,5cm\)

Chiều dài của lò xo khi bị nén là \(l = {l_0} - \Delta l = 10 - 2,5 = 7,5cm\)

Khi treo vật cân bằng trên lò xo, vật chịu tác dụng của hai lực cân bằng: lực đàn hồi và trọng lực, nên F = P

Từ hai lần treo ta có hệ:

\(\left\{ \begin{array}{l}
k.({l_1} - {l_0}) = {P_1}\\
k.({l_2} - {l_0}) = {P_2}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
k.(0,26 - {l_0}) = 0,6.10\\
k.(0,24 - {l_0}) = 0,4.10
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{l_0} = 20cm\\
k = 100N/m
\end{array} \right.\)