Cho khối trụ có hai đáy là \(\left( O \right)\) và \(\left( {O'} \right)\). \(AB,\,\,CD\) lần lượt là hai đường kính của \(\left( O \right)\) và \(\left( {O'} \right)\), góc giữa \(AB\) và \(CD\) bằng \({30^0}\), \(AB = 6\) và thể tích khối tứ diện \(ABCD\) bằng 30. Thể tích khối trụ đã cho bằng:
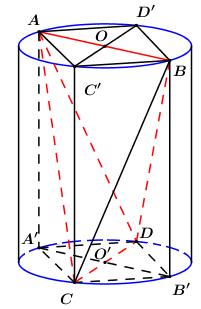
Gọi \(A',\,\,B'\) lần lượt là hình chiếu của \(A,\,\,B\) lên đường tròn \(\left( O \right)\).
\(C',\,\,D'\) lần lượt là hình chiếu của \(C,\,\,D\) lên đường tròn \(\left( {O'} \right)\).
\( \Rightarrow AC'BD'\) là hình bình hành, lại có \(AB = CD = C'D'\) nên \(AC'BD'\) là hình chữ nhật.
Khi đó \(AC'BD'.A'CB'D\) là hình hộp chữ nhật.
Ta có: \({V_{AC'BD'.A'CB'D}} = {V_{ABCD}} + {V_{A.A'CD}} + {V_{B.B'CD}} + {V_{C.C'AB}} + {V_{D.D'AB}}\).
Ta có: \({V_{A.A'CD}} = \dfrac{1}{3}AA'.{S_{A'CD}} = \dfrac{1}{3}AA'.\dfrac{1}{2}{S_{A'CB'D}} = \dfrac{1}{6}{V_{AC'BD'.A'CB'D}}\).
CMTT ta có: \({V_{B.B'CD}} = {V_{C.C'AB}} = {V_{D.D'AB}} = \dfrac{1}{6}{V_{AC'BD'.A'CB'D}}\).
\(\begin{array}{l} \Rightarrow {V_{AC'BD'.A'CB'D}} = {V_{ABCD}} + 4.\dfrac{1}{6}{V_{AC'BD'.A'CB'D}}\\ \Rightarrow {V_{ABCD}} = \dfrac{1}{3}{V_{AC'BD'.A'CB'D}} = 30\\ \Rightarrow {V_{AC'BD'.A'CB'D}} = 90\end{array}\)
Theo bài ra ta có: \(\angle \left( {AB;CD} \right) = {30^0} \Rightarrow \angle \left( {AB;C'D'} \right) = {30^0}\), giả sử \(\angle \left( {AB;C'D'} \right) = \angle AOC' = {30^0}\).
Lại có \(OA = OC' = \dfrac{1}{2}AB = 3\) \( \Rightarrow {S_{OAC'}} = \dfrac{1}{2}OA.OC'.\sin \angle AOC' = \dfrac{1}{2}.3.3.\sin {30^0} = \dfrac{9}{4}\).
\( \Rightarrow {S_{AC'BD'}} = 4{S_{OAC'}} = 9\).
Ta có: \({V_{AC'BD'.A'CB'D}} = AA'.{S_{AC'BD'}}\)\( \Rightarrow 90 = AA'.9 \Leftrightarrow AA' = 10\).
Vậy thể tích khối trụ là \(V = \pi {r^2}h = \pi .O{A^2}.AA' = \pi {.3^2}.10 = 90\pi \).
Cho hình trụ có \(O,\,\,O'\) là tâm hai đáy. Xét hình chữ nhật \(ABCD\) có \(A,\,\,B\) cùng thuộc \(\left( O \right)\) và \(C,\,\,D\) cùng thuộc \(\left( {O'} \right)\) sao cho \(AB = a\sqrt 3 \), \(BC = 2a\) đồng thời \(\left( {ABCD} \right)\) tạo với mặt phẳng đáy hình trụ góc \({60^0}\). Thể tích khối trụ bằng:
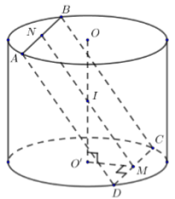
Gọi \(M,\,\,N\) lần lượt là trung điểm của \(CD,\,\,AB\) và \(I\) là trung điểm của \(OO'\).
Ta có:
\(\left\{ \begin{array}{l}\left( {ABCD} \right) \cap \left( {O'CD} \right) = CD\\IM \subset \left( {ABCD} \right),\,\,IM \bot CD\\O'M \subset \left( {O'CD} \right),\,\,O'M \bot CD\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {ABCD} \right);\left( {O'BC} \right)} \right) = \angle \left( {IM;O'M} \right) = \angle IMO' = {60^0}\).
Ta có: \(MN = BC = 2a\) \( \Rightarrow IM = \dfrac{1}{2}MN = a\).
Xét tam giác vuông \(O'IM\) có: \(O'M = IM.\cos {60^0} = \dfrac{a}{2}\), \(O'I = IM.\sin {60^0} = \dfrac{{a\sqrt 3 }}{2}\).
\( \Rightarrow \) Chiều cao của khối trụ là \(h = OO' = 2O'I = a\sqrt 3 \).
Áp dụng định lí Pytago trong tam giác vuông \(O'CM\) có: \(O'C = \sqrt {O'{M^2} + C{M^2}} = \sqrt {\dfrac{{{a^2}}}{4} + \dfrac{{3{a^2}}}{4}} = a\).
\( \Rightarrow \) Bán kính đáy của khối trụ là \(r = O'C = a\).
Vậy thể tích của khối trụ là: \(V = \pi {r^2}h = \pi .{a^2}.a\sqrt 3 = \pi {a^3}\sqrt 3 \).
Thiết diện qua trục của hình trụ là một hình chữ nhật có diện tích bằng 10. Diện tích xung quanh của hình trụ đó bằng:
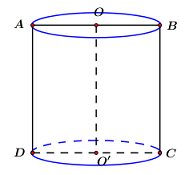
Ta có: \({S_{ABCD}} = AB.AD = 2rh = 10.\)
\( \Rightarrow {S_{xq}} = 2\pi rh = 10\pi .\)
Một cái nồi có dạng hình trụ có chiều cao 60cm và diện tích đáy là \(900\pi \,\,c{m^2}\). Hỏi cần miếng kim loại hình chữ nhật có kích thước bao nhiêu để làm thân nồi?
Ta có hình trụ có diện tích đáy là \(S = \pi {R^2} = 900\pi \Leftrightarrow R = 30\,\,cm\).
Diện tích xung quanh hình trụ là \(S = 2\pi Rh = 2\pi .30.60 = 60\pi .60\,\,\left( {c{m^2}} \right).\)
Vậy cần miếng kim loại hình chữ nhật chiều dài \(60\pi cm\) và chiều rộng \(60\, cm\)
Một sợi dây (không co giãn) được quấn đối xứng đúng 10 vòng quanh một ống trụ tròn đều có bán kính \(R = \dfrac{2}{\pi }\,\,cm\) (như hình vẽ).
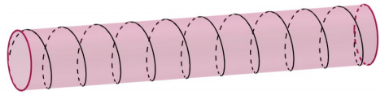
Biết rằng sợi dây có chiều dài 50 cm. Hãy tính diện tích xung quanh của ống trụ đó.
Gọi độ dài đường cao của ống trụ là \(10x\,\,\left( {cm} \right)\,\,\left( {x > 0} \right)\).
Chia ống trụ thành 10 phần bằng nhau, mỗi phần có độ dài đường sinh là \(x\,\,\left( {cm} \right)\).
Trải phẳng mỗi ống trụ nhỏ ta được 1 hình chữ nhật có hai kích thước là \(x\) và \(2\pi .R = 2\pi .\dfrac{2}{\pi } = 4\,\,\left( {cm} \right)\).
Khi đó độ dài đường chéo của hình chữ nhật là \(\sqrt {{x^2} + {4^2}} = \sqrt {{x^2} + 16} \), và độ dài đường chéo chính bằng độ dài của 1 vòng.
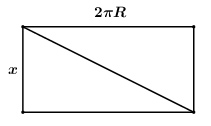
Do đó ta có phương trình: \(10\sqrt {{x^2} + 16} = 50 \Leftrightarrow \sqrt {{x^2} + 16} = 5\) \( \Rightarrow {x^2} + 16 = 25 \Leftrightarrow {x^2} = 9 \Leftrightarrow x = 3\,\,\left( {cm} \right)\,\,\left( {tm} \right)\).
\( \Rightarrow \) Độ dài đường cao của ống trụ là \(h = 10x = 30\,\,\left( {cm} \right)\).
Vậy diện tích xung quanh của ống trụ là \({S_{xq}} = 2\pi Rh = 2\pi .\dfrac{2}{\pi }.30 = 120\,\,\left( {c{m^2}} \right)\).
Cho tứ diện đều ABCD có cạnh bằng 4. Hình trụ \(\left( T \right)\) có một đường tròn đáy là đường tròn nội tiếp tam giác BCD và chiều cao bằng chiều cao của tứ diện ABCD. Diện tích xung quanh của \(\left( T \right)\) bằng:
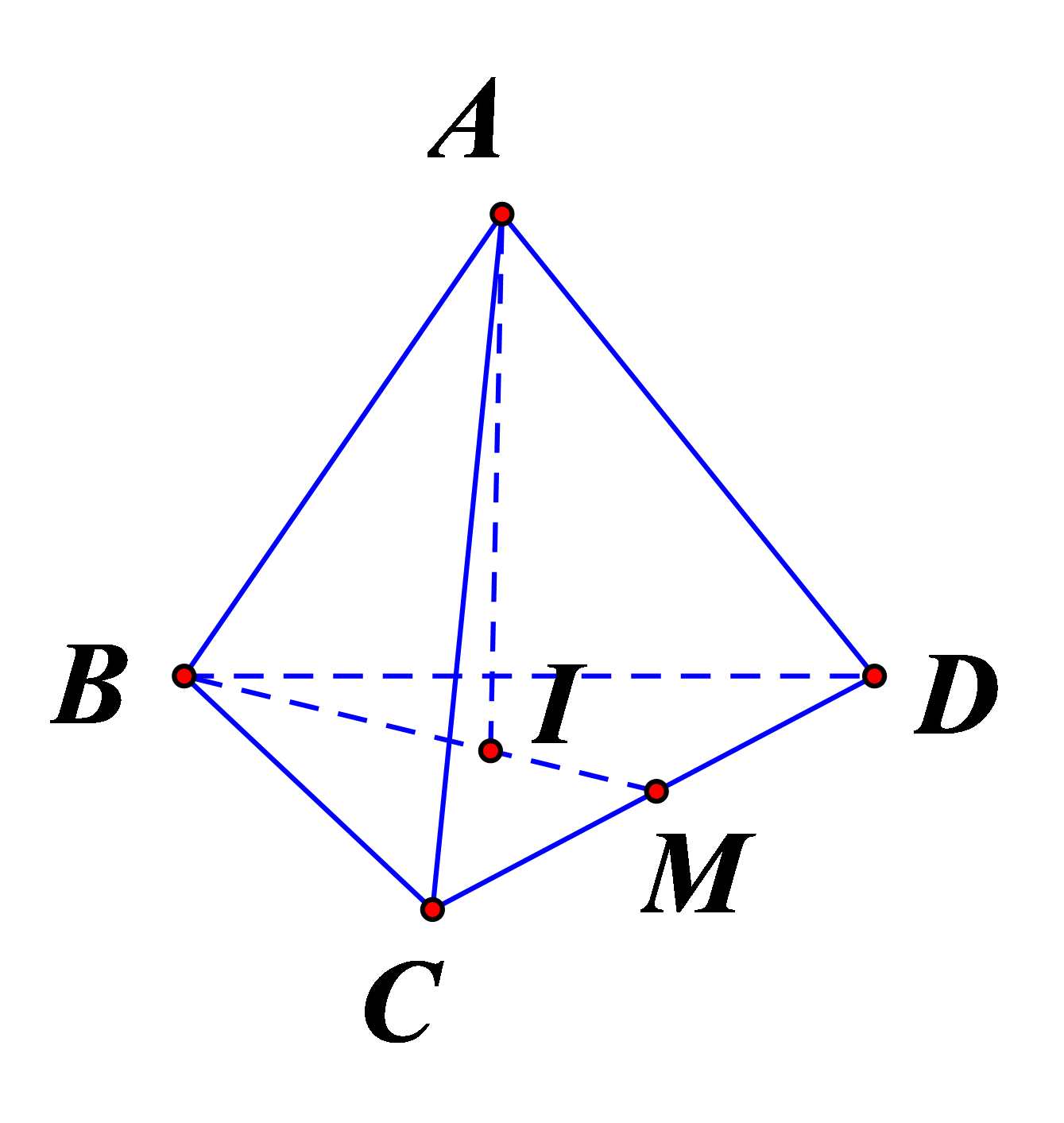
Tam giác BCD là tam giác đều cạnh 4\( \Rightarrow \left\{ \begin{array}{l}{S_{BCD}} = 4\sqrt 3 \\p = 12\end{array} \right.\)
Áp dụng công thức tính bán kính đường tròn nội tiếp ta có:\(R = \dfrac{{2S}}{p} = \dfrac{{2\sqrt 3 }}{3}\)
Gọi O là tâm của tam giác đều BCD
\( \Rightarrow AO \bot \left( {BCD} \right) \Rightarrow \Delta ABO\) vuông tại O có \(BO = \dfrac{{4\sqrt 3 }}{3};AB = 4 \Rightarrow AO = h = \dfrac{{4\sqrt 6 }}{3}\)
Khi đó diện tích xung quanh hình trụ có \(h = \dfrac{{4\sqrt 6 }}{3};R = \dfrac{{2\sqrt 3 }}{3}\) là \(S = 2\pi Rh = \dfrac{{16\sqrt 2 \pi }}{3}\)
Thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình chữ nhật có chu vi bằng 12. Giá trị lớn nhất của thể tích khối trụ bằng
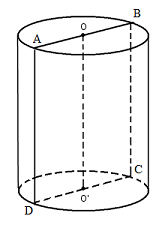
Gọi \(R,\,\,h\) lần lượt là bán kính đáy và chiều cao của hình trụ.
Giả sử thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình chữ nhật \(ABCD\) như hình vẽ, ta có \(AB = 2R\) và \(AD = h\).
Chu vi thiết diện chứa trục bằng 12 \( \Rightarrow 2R + h = 6 \Rightarrow h = 6 - 2R\).
Khi đó thể tích khối trụ:
\(\begin{array}{l}V = \pi {R^2}h = \pi {R^2}\left( {6 - 2R} \right) = \pi .R.R\left( {6 - 2R} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \le \pi .{\left( {\dfrac{{R + R + 6 - 2R}}{3}} \right)^3} = 8\pi \end{array}\)
Dấu “=” xảy ra khi và chỉ khi \(R = 6 - 2R \Leftrightarrow R = 2.\)
Vậy thể tích khối trụ lớn nhất là \(8\pi \) khi \(R = 2\).
Cho hình trụ có chiều cao bằng bán kính đáy và bằng \(5cm.\) Mặt phẳng \(\left( \alpha \right)\) song song với trục, cắt hình trụ theo một thiết diện có chu vi bằng \(26\,cm.\) Khoảng cách từ \(\left( \alpha \right)\) đến trục của hình trụ bằng:
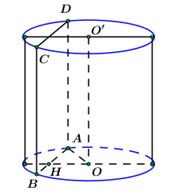
Mặt phẳng \(\left( \alpha \right)\) song song với trục, cắt hình trụ theo thiết diện là một hình chữ nhật \(ABCD\) với \(AD = BC = h = 5.\)
\( \Rightarrow 2\left( {AB + BC} \right) = 2\left( {AB + 5} \right) = 26 \Leftrightarrow AB = 8\,\,cm.\)
Gọi \(H\) là trung điểm của \(AB \Rightarrow OH \bot AB \Rightarrow OH \bot \left( {ABCD} \right)\) hay \(OH \bot \left( \alpha \right).\)
\( \Rightarrow d\left( {OO';\,\,\left( \alpha \right)} \right) = d\left( {O;\,\,\left( \alpha \right)} \right) = OH.\)
\( \Rightarrow AH = \frac{{AB}}{2} = 4\,\,cm.\)
Áp dụng định lý Pitago cho \(\Delta AOH\) vuông tại \(H\) ta có:
\(\begin{array}{l}OH = \sqrt {O{A^2} - A{H^2}} = \sqrt {{5^2} - {4^2}} = 3cm.\\ \Rightarrow d\left( {OO';\,\,\left( \alpha \right)} \right) = 3\,cm.\end{array}\)
Cho hình thang ABCD vuông tại A và D, có AB=3, DC=AD=1. Thể tích của khối tròn xoay nhận được khi quay hình thang ABCD quang trục AB là
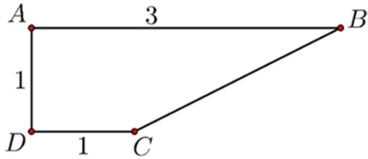
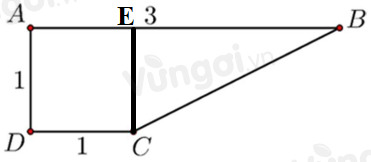
Kẻ CE vuông góc vưới AB (E thuộc AB).
Thể tích khối tròn xoay cần tìm bằng tổng thể tích hai khối tròn xoay khi quay hình vuông ADCE và tam giác vuông ECB quanh trục AB.
Quay hình vuông ADCE ta được khối trụ tròn xoay có chiều cao h=AE=1, bán kính đáy r=AD=1
=> \({V_{TR}} = \pi {r^2}.h = \pi \)(đvtt)
Quay tam giác vuông ECB quanh AB được khối nón có chiều cao h’=EB=3-1=2, bán kính đáy r’=EC=1.
=> \({V_N} = \dfrac{1}{3}.\pi r{'^2}h' = \dfrac{2}{3}\pi \)(đvtt).
Vậy thể tích của khối tròn xoay là \(V = {V_{TR}} + {V_N} = \pi + \dfrac{2}{3}\pi = \dfrac{5}{3}\pi \)(đvtt).
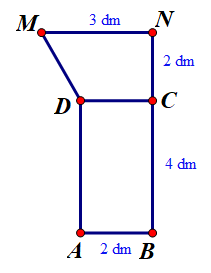
Hình dưới bao gồm hình chữ nhật $ABCD$ và hình thang vuông $CDMN$. Các điểm $B, C, N$ thẳng hàng, $A B=C N=2 \mathrm{dm} ; $$ B C=4 \mathrm{dm}; $$ M N=3 \mathrm{dm}$. Quay hình bên xung quanh cạnh $B N$ ta được khối tròn xoay có thể tích bằng
$\dfrac{86 \pi}{3} \mathrm{dm}^{3}$
$\dfrac{86 \pi}{3} \mathrm{dm}^{3}$
$\dfrac{86 \pi}{3} \mathrm{dm}^{3}$
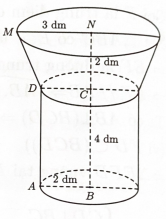
Bước 1: Xác định các hình khối khi quay hình quanh cạnh BN
Khi quay hình trên quanh cạnh $B N$ ta được một khối tròn xoay gồm một khối trụ có bán kính đáy bằng $2 \mathrm{dm}$, chiều cao bằng $4 \mathrm{dm}$ và một khối nón cụt có bán kính hai đáy lần lượt là $2 \mathrm{dm}$ và $3 \mathrm{dm}$, chiều cao bằng $2 \mathrm{dm}$.
Bước 2: Tính thể tích của từng hình (trụ+nón cụt) rồi tính tổng.
Thể tích khối trụ là $V_{T} =4 \pi .4$
Thể tích khối nón cụt là: $V_{N}=\dfrac{2}{3}(4 \pi+9 \pi+\sqrt{4 \pi .9 \pi}$
Do đó thể tích của khối tròn xoay là
$V=4 \pi .4+\dfrac{2}{3}(4 \pi+9 \pi+\sqrt{4 \pi .9 \pi})=\dfrac{86 \pi}{3}\left(\mathrm{dm}^{3}\right)$
Một sợi dây được quấn đối xứng đúng 10 vòng quanh một ống trụ tròn đều có bán kính \(R = \dfrac{2}{\pi }{\rm{cm}}\) (như hình bên dưới)
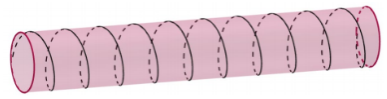
Biết rằng sợi dây dài \(50\;{\rm{cm}}\). Hãy tính diện tích xung quanh của ống trụ đó.
\(120\;{\rm{c}}{{\rm{m}}^2}\)
\(120\;{\rm{c}}{{\rm{m}}^2}\)
\(120\;{\rm{c}}{{\rm{m}}^2}\)

Bước 1: Gọi chiều cao của hình trụ là \(x(\;{\rm{cm}})\). Khi trải phẳng ống trụ và nhận xét kích thước.
Gọi chiều cao của hình trụ là \(x(\;{\rm{cm}})\)
Khi trải phẳng ống trụ tròn đều ta được một hình chữ nhật có chiều rộng là chu vi của mặt đáy còn chiều dài là chiều dài của trụ, mỗi vòng quấn của dây dài \(5\;{\rm{cm}}\) là đường chéo của hình chữ nhật có kích thước lần lượt bằng chu vi đáy trụ (5cm) và \(\dfrac{1}{{10}}\) chiều dài trụ.
Bước 2: Tính diện tích xung quanh ống trụ
Theo định lý Pitago ta có:
\(\sqrt {{5^2} - {{\left( {2 \cdot \dfrac{2}{\pi }\pi } \right)}^2}} = \dfrac{x}{{10}} \Leftrightarrow x = 30(\;{\rm{cm}})\)
Vậy diện tích xung quanh của trụ là: \({S_{xq}} = 2 \cdot \dfrac{2}{\pi } \cdot \pi \cdot 30 = 120\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\).
Cho hình trụ có đường kính đáy bằng 2a. Thiết diện qua trục của hình trụ là hình chữ nhật có đường chéo là 3a. Diện tích toàn phần của hình trụ là
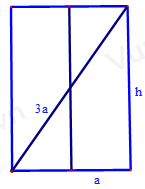
R=a
\(h = \sqrt {{{\left( {3a} \right)}^2} - {{\left( {2a} \right)}^2}} = a\sqrt 5 \)
Diện tích toàn phần là:
\({S_{tp}} = 2\pi {R^2} + 2\pi Rh = 2\pi {a^2} + 2\pi a.a\sqrt 5 = \left( {2 + 2\sqrt 5 } \right)\pi {a^2}\)
Cho lăng trụ tam giác đều ABC.A’B’C’ có thể tích bằng 1. Gọi (T) là hình trụ nội tiếp lăng trụ và M là tâm của mặt bên BCC’B’. Mặt phẳng (P) chứa AM cắt hình trụ (T) như hình vẽ.
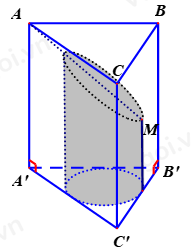
Thể tích khối hình còn lại (phần tô đậm) của khối trụ (T) là
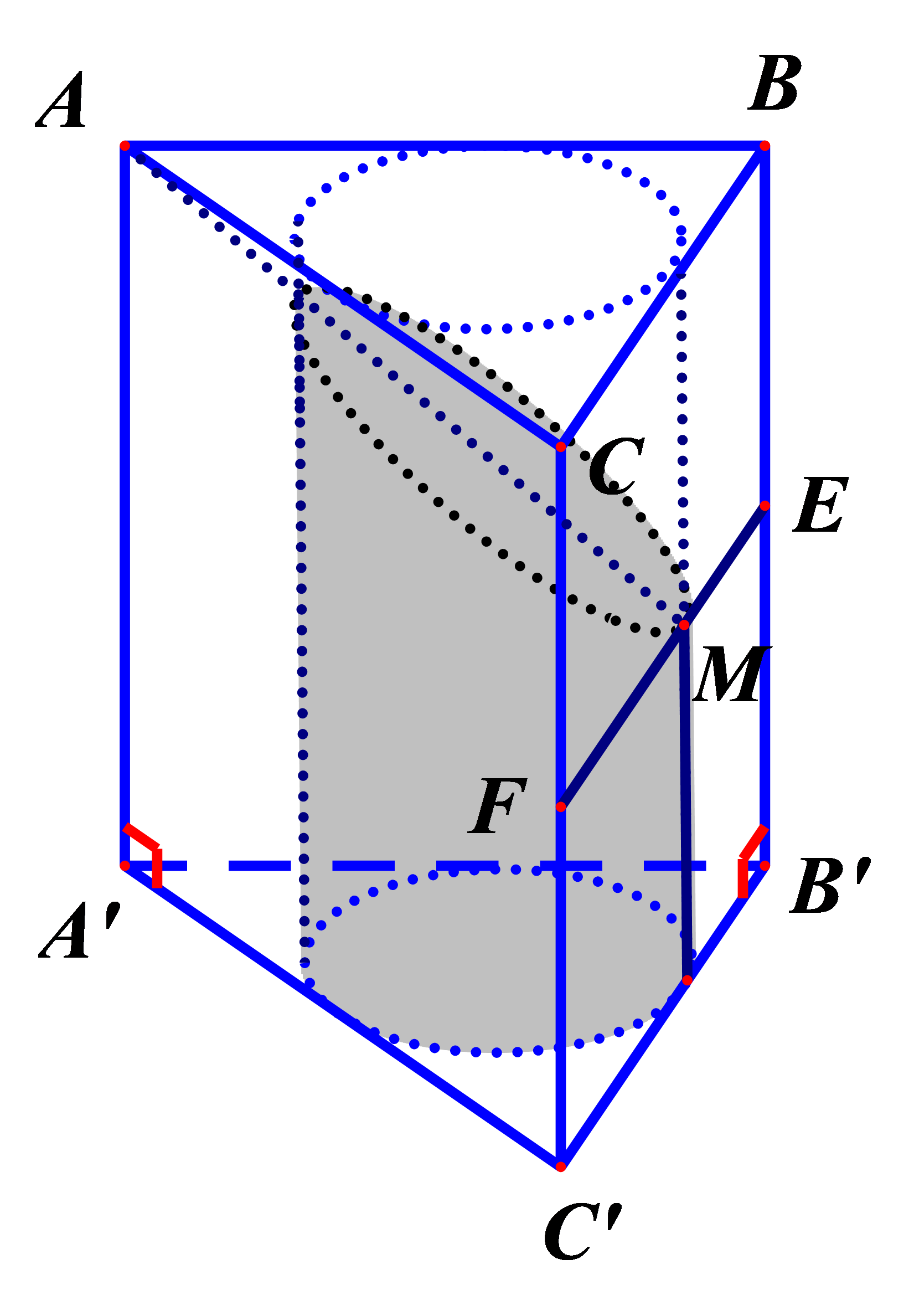
Giả sử h=S=1
Cạnh AB=a, bán kính đường tròn nội tiếp tam giác A’B’C’ là r và p là nửa chu vi của tam giác ABC.
Khi đó ta có: S=p.r=1
Mà
\(\begin{array}{l}p = \dfrac{{3a}}{2};S = \sqrt {p{{\left( {p - a} \right)}^3}} = 1\\ \Rightarrow p{\left( {p - a} \right)^3} = 1 \Leftrightarrow \dfrac{{3a}}{2}{\left( {\dfrac{a}{2}} \right)^3} = 1\\ \Leftrightarrow a = \dfrac{2}{{\sqrt[4]{3}}} \Rightarrow p = \sqrt[4]{{27}} \Rightarrow r = \dfrac{1}{{\sqrt[4]{{27}}}}\\\dfrac{{{V_{tru}}}}{{{V_{ltru}}}} = \dfrac{{{S_{tron}}}}{{{S_{A'B'C'}}}} = \dfrac{{\pi {r^2}}}{{pr}} = \dfrac{{\pi r}}{p} = \dfrac{{\pi .1}}{{\sqrt {27} }}\\ \Rightarrow {V_{tru}} = \dfrac{\pi }{{\sqrt {27} }}\end{array}\)
Gọi thể tích của khối trụ bị cắt bỏ là \({V_1}\) và phần tô đậm của (T) là \({V_2}\)
Mà thiết diện khi lăng trụ bị cắt là tam giác AEF với E và F lần lượt là trung điểm của BB’ và CC’
Khi đó \(\dfrac{{{V_{ABCFE}}}}{{V _{ABC.A'B'C'}}} = \dfrac{{{V_1}}}{{{V_1} + {V_2}}}\)
Ta có:
\(\begin{array}{l}\dfrac{{{V_{ABCFE}}}}{{V _{ABC.A'B'C'}}} = \dfrac{{0 + \dfrac{1}{2} + \dfrac{1}{2}}}{3} = \dfrac{1}{3}\\ \Rightarrow \dfrac{{{V_1}}}{{{V_1} + {V_2}}} = \dfrac{1}{3} \Rightarrow \dfrac{{{V_2}}}{{{V_1} + {V_2}}} = \dfrac{2}{3}\\ \Rightarrow {V_2} = \dfrac{2}{3}.{V_{tru}} = \dfrac{2}{3}.\dfrac{\pi }{{\sqrt {27} }} = \dfrac{{2\pi \sqrt 3 }}{{27}}\end{array}\)
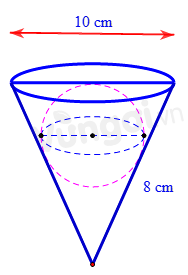
Bạn An có một cốc hình nón có đường kính đáy là 10cm và độ dài đường sinh là 8cm. Bạn dự định đựng một viên bị hình cầu sao cho toàn bộ viên bi nằm trong cốc (không phân nào của viên bị cao hơn miệng cốc). Hỏi bạn An có thể đựng được viên bị có đường kính lớn nhất bằng bao nhiêu?
Bước 1: Xét thiết diện qua trục.
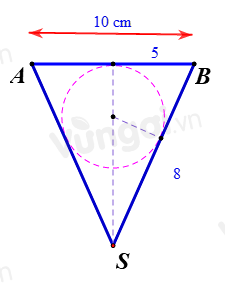
Thiết diện qua trục là một tam giác cân có cạnh bên là 8cm và cạnh đáy là 10 cm (tam giác SAB)
Bước 2: Xác định vị trí của viên bi thỏa mãn bài toán
Viên bi bị cắt theo chính thiết diện đó thì sẽ tiếp xúc với hai cạnh bên.
Viên bi càng tiến gần đáy thì càng lớn.
Để viên bị có đường kính lớn nhất thì viên bi phải tiếp xúc với mặt trên của cốc nước (miễn là viên bi không cao hơn miệng cốc)
Bước 3: Tính đường kính viên bi
\(p = \dfrac{{8 + 8 + 10}}{2} = 13\)
\(\begin{array}{l}r = \dfrac{S}{p} = \dfrac{{5\sqrt {{8^2} - {5^2}} }}{{13}} = \dfrac{{5\sqrt {39} }}{{13}}\\d = 2r = \dfrac{{10\sqrt {39} }}{{13}}\left( {cm} \right)\end{array}\)

