Cho hai véc tơ \(\overrightarrow {OA} = \left( { - 1;2; - 3} \right),\overrightarrow {OB} = \left( {2; - 1;0} \right)\), khi đó tổng hai véc tơ \(\overrightarrow {OA} ,\overrightarrow {OB} \) là:
Ta có: \(\overrightarrow {OA} = \left( { - 1;2; - 3} \right),\overrightarrow {OB} = \left( {2; - 1;0} \right) \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} = \left( {1;1; - 3} \right)\).
Cho véc tơ \(\overrightarrow u = \left( {x;y;z} \right)\) và số thực \(k\). Khi đó:
Ta có: \(k\overrightarrow u = \left( {kx;ky;kz} \right)\)
Trong không gian với hệ tọa độ $Oxyz$, cho vectơ \(\vec c = - 9\vec k\). Tọa độ của vectơ \(\vec c\) là:
Ta có: \(\vec k = \left( {0;0;1} \right) \Rightarrow \vec c = - 9\vec k = \left( {0;0; - 9} \right)\)
Cho các véc tơ \(\overrightarrow {{u_1}} = \left( {{x_1};{y_1};{z_1}} \right),\overrightarrow {{u_2}} = \left( {{x_2};{y_2};{z_2}} \right)\). Khi đó:
Ta có: \(\overrightarrow {{u_1}} .\overrightarrow {{u_2}} = {x_1}{x_2} + {y_1}{y_2} + {z_1}{z_2}\).
Cho hai véc tơ \(\overrightarrow u = \left( { - 2;3;1} \right)\) và \(\overrightarrow v = \left( {1;1;1} \right)\). Khi đó số thực \(m = \overrightarrow u .\overrightarrow v \) thỏa mãn:
Ta có: \(m = \overrightarrow u .\overrightarrow v = - 2.1 + 3.1 + 1.1 = 2 \Rightarrow m \in \left( {1;3} \right)\).
Công thức tính độ dài véc tơ \(\overrightarrow u = \left( {a;b;c} \right)\) là:
Ta có: \(\left| {\overrightarrow u } \right| = \sqrt {{{\overrightarrow u }^2}} = \sqrt {{a^2} + {b^2} + {c^2}} \)
Trong không gian với hệ tọa độ Oxyz, cho ba vector $\vec a = \left( {2;3; - 5} \right);{\mkern 1mu} {\mkern 1mu} \vec b = \left( {0; - 3;4} \right);{\mkern 1mu} {\mkern 1mu} \vec c = \left( {1; - 2;3} \right)$. Tọa độ vector $\vec n = 3\vec a + 2\vec b - \vec c$ là:
$\vec n = 3\left( {2;3; - 5} \right) + 2\left( {0; - 3;4} \right) - \left( {1; - 2;3} \right) = \left( {5;5; - 10} \right)$
Cho hai véc tơ \(\overrightarrow {{u_1}} \left( {{x_1};{y_1};{z_1}} \right),\overrightarrow {{u_2}} \left( {{x_2};{y_2};{z_2}} \right)\). Hai véc tơ vuông góc với nhau thì điều gì sau đây không xảy ra?
\(\overrightarrow {{u_1}} \bot \overrightarrow {{u_2}} \Leftrightarrow \cos \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right) = 0 \Leftrightarrow \overrightarrow {{u_1}} .\overrightarrow {{u_2}} = 0 \Leftrightarrow {x_1}{x_2} + {y_1}{y_2} + {z_1}{z_2} = 0\)
Cho hai véc tơ \(\overrightarrow u = \left( {2;1; - 3} \right),\overrightarrow v = \left( {0;b;1} \right)\), nếu \(\overrightarrow u \bot \overrightarrow v \) thì:
Ta có: \(\overrightarrow u \bot \overrightarrow v \Leftrightarrow \overrightarrow u .\overrightarrow v = 2.0 + 1.b + \left( { - 3} \right).1 = 0 \Leftrightarrow b = 3\).
Cho các véc tơ \(\overrightarrow {{u_1}} \left( {{x_1};{y_1};{z_1}} \right)\) và $\overrightarrow {{u_2}} \left( {{x_2};{y_2};{z_2}} \right),$ khi đó cô sin góc hợp bởi hai véc tơ \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) là:
Cô sin của góc hợp bởi hai véc tơ \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) là: \(\cos \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right) = \dfrac{{\overrightarrow {{u_1}} .\overrightarrow {{u_2}} }}{{\left| {\overrightarrow {{u_1}} } \right|.\left| {\overrightarrow {{u_2}} } \right|}} = \dfrac{{{x_1}{x_2} + {y_1}{y_2} + {z_1}{z_2}}}{{\sqrt {x_1^2 + y_1^2 + z_1^2} .\sqrt {x_2^2 + y_2^2 + z_2^2} }}\)
Cho hai véc tơ \(\overrightarrow u = \left( { - 1; - 1; - 1} \right),\overrightarrow v = \left( {2;1;0} \right)\), khi đó cô sin của góc hợp bởi hai véc tơ đó là:
Ta có:
\(\cos \left( {\overrightarrow u ,\overrightarrow v } \right) = \dfrac{{ - 1.2 - 1.1 - 1.0}}{{\sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 1} \right)}^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{2^2} + {1^2} + {0^2}} }} \)
$= - \dfrac{3}{{\sqrt {15} }} = - \dfrac{{3\sqrt {15} }}{{15}} = - \dfrac{{\sqrt {15} }}{5}$
Cho hai điểm \(A\left( {{x_A};{y_A};{z_A}} \right),B\left( {{x_B};{y_B};{z_B}} \right)\), khi đó véc tơ \(\overrightarrow {AB} \) có tọa độ:
Điểm \(A\left( {{x_A};{y_A};{z_A}} \right),B\left( {{x_B};{y_B};{z_B}} \right)\) có \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}} \right)\).
Cho hai điểm \(A\left( {5;3;1} \right),B\left( {1;3;5} \right)\). Độ dài véc tơ \(\overrightarrow {AB} \) là:
Ta có: \(\overrightarrow {AB} = \left( { - 4;0;4} \right) \Rightarrow \left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( { - 4} \right)}^2} + {0^2} + {4^2}} = 4\sqrt 2 \)
Cho hai điểm \(A\left( {{x_A};{y_A};{z_A}} \right),B\left( {{x_B};{y_B};{z_B}} \right)\), khi đó độ dài đoạn thẳng \(AB\) được tính theo công thức:
Cho hai điểm \(A\left( {{x_A};{y_A};{z_A}} \right),B\left( {{x_B};{y_B};{z_B}} \right)\), khi đó độ dài đoạn thẳng \(AB\) được tính theo công thức: \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \)
Độ dài đoạn thẳng \(AB\) với \(A\left( {2;1;0} \right),B\left( {4; - 1;1} \right)\) là một số:
Ta có: \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \)
$= \sqrt {{{\left( {4 - 2} \right)}^2} + {{\left( { - 1 - 1} \right)}^2} + {{\left( {1 - 0} \right)}^2}} = \sqrt 9 = 3$
Do đó độ dài đoạn thẳng là một số nguyên dương.
Cho hai vectơ \(\overrightarrow a = \left( {1;1; - 2} \right),\,\,\overrightarrow b = \left( {1;0;m} \right)\). Góc giữa chúng bằng \({45^0}\) khi:
Góc giữa $\overrightarrow u ;\overrightarrow v$ bằng \({45^0}\) khi \(\cos \left( {\overrightarrow u ;\overrightarrow v } \right) =\cos 45^0\)
Mà \(\cos \left( {\overrightarrow u ;\overrightarrow v } \right) = \dfrac{{\overrightarrow u .\overrightarrow v }}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|}}\)
\(\begin{array}{l} \Rightarrow \cos {45^0} = \dfrac{{1.1 + 1.0 - 2.m}}{{\sqrt {{1^2} + {1^2} + {{\left( { - 2} \right)}^2}} .\sqrt {{1^2} + {0^2} + {m^2}} }}\\ \Leftrightarrow \dfrac{1}{{\sqrt 2 }} = \dfrac{{1 - 2m}}{{\sqrt 6 .\sqrt {1 + {m^2}} }} \Leftrightarrow \sqrt {6\left( {1 + {m^2}} \right)} = \sqrt 2 \left( {1 - 2m} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}6\left( {1 + {m^2}} \right) = 2{\left( {1 - 2m} \right)^2}\\1 - 2m \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}6 + 6{m^2} = 2\left( {1 - 4m + 4{m^2}} \right)\\m \le \dfrac{1}{2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}6 + 6{m^2} = 2 - 8m + 8{m^2}\\m \le \dfrac{1}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2{m^2} - 8m - 4 = 0\\m \le \dfrac{1}{2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m = 2 \pm \sqrt 6 \\m \le \dfrac{1}{2}\end{array} \right. \Leftrightarrow m = 2 - \sqrt 6 \end{array}\)
Trong không gian Oxyz, cho hình hộp ABCD.A’B’C’D’ có A(0;0;1), B’(1;0;0), C’(1;1;0). Tìm tọa độ điểm D.
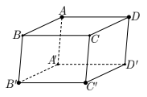
Ta có AD // B’C’, AD = B’C’ nên AB’C’D là hình bình hành, do đó AB’ // DC’ và AB’ = DC’.
\(\begin{array}{l} \Rightarrow \overrightarrow {AB'} = \overrightarrow {DC'} \\ \Rightarrow \left\{ \begin{array}{l}1 - 0 = 1 - {x_D}\\0 - 0 = 1 - {y_D}\\0 - 1 = 0 - {z_D}\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}{x_D} = 0\\{y_D} = 1\\{z_D} = 1\end{array} \right.\end{array}\)
Vậy \(D\left( {0;1;1} \right)\).
Cho 3 điểm A(0;0;1), B(1;0;0); C(1;1;0). Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Bước 1: Tính độ dài cạnh AB, BC, CA.
Ta có:
\(\begin{array}{l}AB = \sqrt {{1^2} + {0^2} + {{\left( { - 1} \right)}^2}} = \sqrt 2 \\BC = \sqrt {{0^2} + {1^2} + {0^2}} = 1\\CA = \sqrt {{1^2} + {1^2} + {{\left( { - 1} \right)}^2}} = \sqrt 3 \end{array}\)
\( \Rightarrow \Delta ABC\) là tam giác vuông tại B.
Bước 2: Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Ta có \(R = \dfrac{{AC}}{2} = \dfrac{{\sqrt 3 }}{2}\)
