Phát biểu nào sau đây là đúng nhất khi nói về khái niệm gia tốc?
Cả A, B, C đều đúng
Trong công thức liên hệ giữa quãng đường đi được, vận tốc và gia tốc của chuyển động nhanh dần đều \({v^2} - v_0^2 = 2{\rm{as}}\), ta có các điều kiện nào sau đây?
Công thức \({v^2} - v_0^2 = 2{\rm{as}}\) chỉ đúng khi chuyển động là không đổi chiều. Với v > v0 => vật chuyển động theo chiều dương, chuyển động là nhanh dần nên a và v cùng chiều do vậy a > 0, quãng đường s là một đại lượng không âm
Chọn câu đúng?
Từ các phương trình vận tốc cho biết tính chất các chuyển động sau
A - sai vì chuyển động thẳng đều có vận tốc không đổi
B - sai vì: \(a = 3,{v_0} = 0\) => vật chuyển động nhanh dần
C - sai vì \(a = - 2;{v_0} = 9\) => vật chuyển động chậm dần
D- đúng
Đặc điểm nào sau đây sai với chuyển động thẳng nhanh dần đều?
A, C, D - đúng
B - sai vì: Vận tốc của vật âm hay dương phụ thuộc vào chiều chuyển động của vật so với chiều dương của trục tọa độ mà ta chọn.
Chọn đáp án sai? Chất điểm chuyển động thẳng theo một chiều với gia tốc \(a = 4m/{s^2}\) có nghĩa là:
Ta có: Vận tốc được xác định bằng biểu thức \(v = {v_0} + at\)
A, B, D - đúng
C -sai vì: \(v = {v_0} + at \to v = 2 + 4.2 = 10m/s\left( {{v_0} = 2,t = 2} \right)\)
Phương trình chuyển động của một vật trên một đường thẳng có dạng \(x = 2{t^2} + 10t + 100(m;s)\).Thông tin nào sau đây là đúng?
Từ phương trình chuyển động ta có: \(\left\{ \begin{array}{l}{x_0} = 100m\\{v_0} = 10m/s\\a = 4m/{s^2}\end{array} \right.\)
=> Vật chuyển động nhanh dần đều với gia tốc \(a = 4{\rm{ }}m/{s^2}\)
Tọa độ lúc ban đầu của vật là \({x_0} = 100m\)
Vận tốc của vật tại thời điểm ban đầu: \({v_0} = 10m/s\)
Phương trình chuyển động của một vật trên một đường thẳng có dạng \(x = 4{t^2} - 3t + 7(m;s)\). Điều nào sau đây là sai?
Ta có: Gia tốc của vật là: a = 8m/s2
=> A - sai
Đồ thị tọa độ theo thời gian của chất điểm chuyển động thẳng biến đổi đều có dạng
Ta có phương trình tọa độ theo thời gian của chất điểm trong chuyển đông thẳng biến đổi đều có dạng: \(x = {x_0} + {v_0}t + \dfrac{1}{2}a{t^2}\)
=> Đồ thị của tọa độ theo thời gian của chất điểm chuyển động thẳng biến đổi đều là một nhánh parabol (dạng đồ thị giống hàm \(y = ax^2+bx+c\) nhưng ở đây ta có t>0 lên đồ thị chỉ là một nhánh parabol)
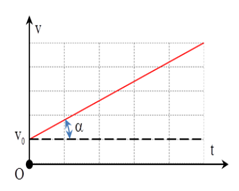
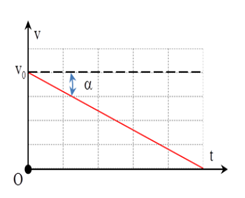
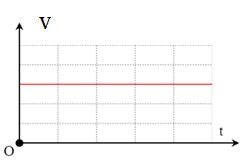
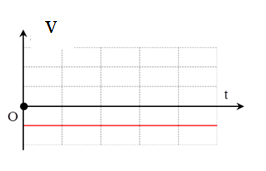
Đồ thị v - t nào sau đây là đồ thị trong đó a > 0
Đồ thị v - t trong đó a > 0 là đồ thị A
Đồ thị a - t của chuyển động thẳng biến đổi đều có dạng:
Đồ thị a - t của chất điểm chuyển động thẳng biến đổi đều có dạng là đường thẳng song song với trục Ot
Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc \({v_1}\left( t \right) = 7t\,\,\left( {m/s} \right)\). Đi được 5s, người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc \(a = - 70\,\,\left( {m/{s^2}} \right)\). Tính quãng đường S đi được của ô tô lúc bắt đầu chuyển bánh cho đến khi dừng hẳn.
Quãng đường ô tô đi được 5s đầu là: \({S_1} = \int\limits_0^5 {{v_1}\left( t \right)\,dt} = \int\limits_0^5 {7t\,dt} = \left. {\dfrac{1}{2}.7{t^2}} \right|_0^5 = 87,5\,\left( m \right)\)
Vận tốc khi xe đi được 5s là: \({v_1}\left( 5 \right) = 7.5 = 35\left( {m/s} \right)\)
Phương trình vận tốc của xe khi xe gặp chướng ngại vật là: \({v_2}\left( t \right) = 35 - 70t\,\left( {m/s} \right)\)
Thời gian ô tô di chuyển tiếp đến khi dừng hẳn: \(35 - 70t = 0 \Leftrightarrow t = \dfrac{1}{2}\left( s \right)\)
Quãng đường ô tô đi tiếp cho đến khi dừng hẳn là: \({S_2} = \int\limits_0^{\dfrac{1}{2}} {{v_2}\left( t \right)\,dt} = \int\limits_0^{\dfrac{1}{2}} {\left( {35 - 70t} \right)dt} \)\( = \left. {\left( {35t - 35{t^2}} \right)} \right|_0^2 = 8,75\,\left( m \right).\)
Tổng quãng đường cần tìm là: \(87,5 + 8,75 = 96,25\left( m \right)\).