Các bài toán về mặt cầu và mặt phẳng

$(S)$ có tâm $I(–1;2;1)$ và $R = 1$.

Gọi $\overrightarrow v \left( {t;0;t} \right)$là vectơ cùng phương với vectơ $\overrightarrow u \left( {1;0;1} \right)$ sao cho phép tịnh tiến vectơ đó biến $(S)$ thành $(S’)$ tiếp xúc với $(P)$

Phép tịnh tiến vectơ $\overrightarrow v \left( {t;0;t} \right)$ biến $I$ thành $I’ (–1 + t; 2; 1 + t)$

Suy ra $(S’)$ có tâm $I’$ và bán kính $R’ = R = 1$.

$(S’)$ tiếp xúc $(P)$ $ ⇔ d(I; (P)) = 1 \Leftrightarrow \dfrac{{\left| { - 1 + t - 2.2 + 2\left( {1 + t} \right) - 3} \right|}}{{\sqrt {1 + 4 + 4} }} = 1 \Leftrightarrow \left| {3t - 6} \right| = 3 \Leftrightarrow \left[ \begin{array}{l}t = 3\\t = 1\end{array} \right.$

Với $t = 3 \Rightarrow \overrightarrow v \left( {3;0;3} \right) \Rightarrow \left| {\overrightarrow v } \right| = 3\sqrt 2 $

Với $t = 1 ⇒ \overrightarrow v \left( {1;0;1} \right) \Rightarrow \left| {\overrightarrow v } \right| = \sqrt 2 $

Vậy giá trị lớn nhất của $MN $ là $3\sqrt 2 $

Mặt cầu $\left( S \right)$ có tâm $I\left( { - 1;2; - 3} \right)$ và bán kính $R = 3$

Ta có : $M( - 1;2;0) \in \left( S \right)$

Gọi $\left( \alpha  \right)$  là mặt phẳng tiếp diện của $\left( S \right)$  tại $M$.

Khi đó $\left( \alpha  \right)$  đi qua $M$ và nhận $\overrightarrow {IM} \left( {0;0;3} \right)$ làm véctơ pháp tuyến

Vậy $\left( \alpha  \right):0(x + 1) + 0(y - 2) + 3(z - 0) = 0 \Leftrightarrow z = 0$

Giả sử $M(a;b;c)$ là điểm cần tìm.

Mặt cầu $(S)$ có tâm $I(1;2;3)$ bán kính $R=3 $.
Gọi $Δ$ là đường thẳng qua $I$ và vuông góc với $mp(P)$.

\( \Rightarrow \)\(\Delta :\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 - 2t\\z = 3 + t\end{array} \right.\)
Đường thẳng $Δ$ cắt mặt cầu tại 2 điểm $A, B$. Toạ độ $A, B$ là nghiệm của hệ:

\(\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 - 2t\\z = 3 + t\\{(x - 1)^2} + {(y - 2)^2} + {(z - 3)^2} = 9\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = 1\\t =  - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}A\left( {3;0;4} \right)\\B\left( { - 1;4;2} \right)\;\end{array} \right.\)

Ta có:  $d\left( {A;\left( P \right)} \right) = \dfrac{{\left| {2.3 - 2.0 + 4 + 3} \right|}}{{\sqrt {{2^2} + {2^2} + 1} }} = \dfrac{{13}}{3}$ và  $d\left( {B;\left( P \right)} \right) = \dfrac{{\left| {2.( - 1) - 2.4 + 2 + 3} \right|}}{{\sqrt {{2^2} + {2^2} + 1} }} = \dfrac{5}{3}$

Do đó điểm cần tìm là điểm $A≡M \Rightarrow a+b+c= 3+0+4= 7$.

$(S)$ có tâm $I(5;-3;7)$ và bán kính $R= 6\sqrt 2 $

Theo đề bài ta có phương trình $(P)$ có dạng $x+m(y-8)+n(z-2)=0$

Vì $(P)$ tiếp xúc với $(S) $ nên ${\rm{d}}(I,(P)) = \dfrac{{\left| {5 + m( - 3 - 8) + n(7 - 2)} \right|}}{{\sqrt {1 + {m^2} + {n^2}} }} = \dfrac{{\left| {5 - 11m + 5n} \right|}}{{\sqrt {1 + {m^2} + {n^2}} }} = 6\sqrt 2 $

                                                      $\begin{array}{l} \Leftrightarrow \left| {5 - 11m + 5n} \right| = 6\sqrt 2 .\sqrt {1 + {m^2} + {n^2}} \\ \Leftrightarrow 25 + 121{m^2} + 25{n^2} - 110m + 50n - 110mn = 72(1 + {m^2} + {n^2})\\ \Leftrightarrow 49{m^2} - 110m + 50n - 110mn - 47{n^2} - 47 = 0\\ \Leftrightarrow 49{m^2} - 110m(n + 1) - 47{n^2} + 50n - 47 = 0(1)\\\Delta ' = 3025{(n + 1)^2} - 49( - 47{n^2} + 50n - 47) = 5328{n^2} + 3600n + 5328 > 0\end{array}$

Phương trình (*) luôn có  nghiệm

$\begin{array}{l}{\rm{d}}(B,(P)) = \dfrac{{\left| {1 + m(1 - 8) + n( - 9 - 2)} \right|}}{{\sqrt {1 + {m^2} + {n^2}} }} = \dfrac{{\left| {1 - 7m - 11n} \right|}}{{\sqrt {1 + {m^2} + {n^2}} }}\\ =  > d(B,(P))\max  = AB \Leftrightarrow \dfrac{{\left| {1 - 7m - 11n} \right|}}{{\sqrt {1 + {m^2} + {n^2}} }} = 3\sqrt {19}  \Leftrightarrow \sqrt {1 + {m^2} + {n^2}}  = \dfrac{{\left| {1 - 7m - 11n} \right|}}{{3\sqrt {19} }}\end{array}$

Mặt khác $\dfrac{{\left| {5 - 11m + 5n} \right|}}{{6\sqrt 2 }} = \sqrt {1 + {m^2} + {n^2}} $

$\dfrac{{\left| {1 - 7m - 11n} \right|}}{{3\sqrt {19} }}$=$\dfrac{{\left| {5 - 11m + 5n} \right|}}{{6\sqrt 2 }}$

      $\begin{array}{l}72(1 + 49{m^2} + 121{n^2} - 14m - 22n + 154mn) = 171(25 + 121{m^2} + 25{n^2} - 110m + 50n - 110mn)\\ \Leftrightarrow 8(1 + 49{m^2} + 121{n^2} - 14m - 22n + 154mn) = 19(25 + 121{m^2} + 25{n^2} - 110m + 50n - 110mn)\\ \Leftrightarrow  - 1907{m^2} + 493{n^2} + 1978m - 1126n + 3322mn - 467 = 0(2)\end{array}$

Từ (1) và (2) $\Rightarrow m.n= \dfrac{{276}}{{49}}$

Mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} + 6x - 4z + 9 - {m^2} = 0\) có tâm \(I\left( { - 3;0;2} \right)\) và bán kính \(R = \sqrt {{m^2} + 4} \)

Mặt phẳng \(\left( {Oyz} \right)\) có phương trình là \(x = 0 \Rightarrow d\left( {I;\left( {Oyz} \right)} \right) = \frac{{\left| { - 3} \right|}}{1} = 3\)

\( \Rightarrow R = \sqrt {{m^2} + 4}  = 3 \Leftrightarrow m =  \pm \sqrt 5 \)

Tích các giá trị của m là \(\sqrt 5 .\left( { - \sqrt 5 } \right) =  - 5\).

Vì \(I \in \Delta :\,\,\dfrac{{x - 1}}{{ - 2}} = \dfrac{y}{2} = \dfrac{{z - 2}}{1}\) nên ta gọi \(I\left( {1 - 2t;\,\,2t;\,\,2 + t} \right)\).

Vì \(\left( S \right)\) tiếp xúc với \(\left( P \right):\,\,2x - y + z - 3 = 0\) tại điểm \(H\left( {1; - 1;0} \right)\) nên ta có: \(d\left( {I;\left( P \right)} \right) = IH = R\).

\(\begin{array}{l} \Leftrightarrow \dfrac{{\left| {2.\left( {1 - 2t} \right) - 2t + 2 + t - 3} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {1^2}} }} = \sqrt {{{\left( {2t} \right)}^2} + {{\left( { - 1 - 2t} \right)}^2} + {{\left( { - 2 - t} \right)}^2}} \\ \Leftrightarrow \dfrac{{\left| { - 5t + 1} \right|}}{{\sqrt 6 }} = \sqrt {9{t^2} + 8t + 5} \\ \Leftrightarrow 25{t^2} - 10t + 1 = 54{t^2} + 48t + 30\\ \Leftrightarrow 29{t^2} + 58t + 29 = 0\\ \Leftrightarrow {t^2} + 2t + 1 = 0\\ \Leftrightarrow {\left( {t + 1} \right)^2} = 0\\ \Leftrightarrow t =  - 1\end{array}\)

\( \Rightarrow I\left( {3; - 2;1} \right)\) và \(R = IH = \sqrt 6 \).

Vậy phương trình mặt cầu \(\left( S \right)\) là: \({\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 1} \right)^2} = 6\).

Đường thẳng \(\Delta :\,\,\dfrac{{x - 1}}{3} = \dfrac{y}{{ - 2}} = \dfrac{{z + 2}}{{ - 1}}\) có 1 VTCP là \(\overrightarrow u  = \left( {3; - 2; - 1} \right)\).

Vì \(\left( \alpha  \right) \bot \Delta \) nên mặt phẳng \(\left( \alpha  \right)\) có 1 VTPT là \(\overrightarrow n  = \overrightarrow u  = \left( {3; - 2; - 1} \right)\). Khi đó phương trình mặt phẳng \(\left( \alpha  \right)\) có dạng \(3x - 2y - z + d = 0\).

Mặt cầu \(\left( S \right):\,\,{x^2} + {y^2} + {z^2} - 8x + 2y + 2z - 3 = 0\) có tâm \(I\left( {4; - 1; - 1} \right)\), bán kính \(R = \sqrt {16 + 1 + 1 + 3}  = \sqrt {21} \).

Gọi \(r\) là bán kính đường tròn \(\left( C \right)\), \(d = d\left( {I;\left( \alpha  \right)} \right)\).

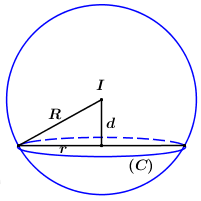
Áp dụng định lí Pytago ta có: \({R^2} = {r^2} + {d^2}\), do đó để \(r\) đạt GTLN thì \(d\) phải đạt GTNN (vì \(R = \sqrt {21} \) không đổi).

Ta có: \(d = \dfrac{{\left| {3.4 - 2.\left( { - 1} \right) - 1.\left( { - 1} \right) + d} \right|}}{{\sqrt {{3^2} + {{\left( { - 2} \right)}^2} + {{\left( { - 1} \right)}^2}} }} = \dfrac{{\left| {15 + d} \right|}}{{\sqrt {14} }} \ge 0\), suy ra \({d_{\min }} = 0 \Leftrightarrow d =  - 15\).

Vậy phương trình mặt phẳng \(\left( \alpha  \right)\) cần tìm là: \(3x - 2y - z - 15 = 0\).

Bước 1:

Dễ dàng nhận thấy \(O,\,\,A,\,\,B\) đều nằm ngoài mặt cầu \(\left( C \right)\) nên \(\left( {OAB} \right)\) không cắt mặt cầu \(\left( C \right)\).

Mặt cầu \(\left( C \right)\) ta có tâm \(I\left( { - 1;3;2} \right)\), bán kính \(R = 1\).

Ta có \(\overrightarrow {OA}  = \left( {2;1;0} \right),\,\,\overrightarrow {OB}  = \left( {0;2;0} \right) \Rightarrow \left[ {\overrightarrow {OA} ;\overrightarrow {OB} } \right] = \left( {0;0;4} \right)\)

\( \Rightarrow {S_{\Delta OAB}} = \dfrac{1}{2}\left| {\left[ {\overrightarrow {OA} ;\overrightarrow {OB} } \right]} \right| = 2\)

Bước 2:

\( \Rightarrow {V_{S.OAB}} = \dfrac{1}{3}d\left( {S;\left( {OAB} \right)} \right).{S_{\Delta OAB}}\).

Vì \({S_{\Delta OAB}}\) không đổi nên \({V_{S.OAB}}\) đạt giá trị lớn nhất khi và chỉ khi \(d\left( {S;\left( {OAB} \right)} \right)\) lớn nhất, khi đó \(d\left( {S;\left( {OAB} \right)} \right) = R + d\left( {I;\left( {OAB} \right)} \right)\).

Bước 3:

Mặt phẳng \(\left( {OAB} \right)\) nhận \(\overrightarrow n  = \dfrac{1}{4}\left[ {\overrightarrow {OA} ;\overrightarrow {OB} } \right] = \left( {0;0;1} \right)\) là 1 VTPT nên có phương trình: \(z = 0\).

\( \Rightarrow d\left( {I;\left( {OAB} \right)} \right) = \left| {{z_I}} \right| = 2\) \( \Rightarrow d{\left( {S;\left( {OAB} \right)} \right)_{\max }} = 1 + 2 = 3\).

Vậy \(\max {V_{S.OAB}} = \dfrac{1}{3}.3.2 = 2\).

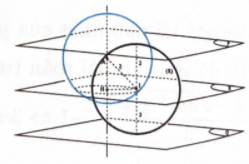
Bước 1: Tính $d((P),(Q))$

Ta thấy $M(1 ; 0 ; 0)$ là một điểm thuộc $(P)$

Vì \((P)//(Q)\) nên \(d((P),(Q)) = d(M,(Q)) \)\(= \dfrac{{|2 + 10|}}{{\sqrt {{2^2} + {{( - 1)}^2} + {{( - 2)}^2}} }} = 4\)

Bước 2: Giả sử $I(a ; b ; c)$ là tâm của $(S)$. Chứng minh $I$ luôn thuộc mặt phẳng $(R)$

Giả sử $I(a ; b ; c)$ là tâm của $(S)$. Vì $(S)$ tiếp xúc với cả $(P)$ và $(Q)$ nên bán kính mặt cầu $(S)$ là $R=\dfrac{d((P),(Q))}{2}=\dfrac{4}{2}=2$

Do đó $I A=2$ nên $I$ luôn thuộc mặt cầu $(T)$ tâm $A$, bán kính 2

Ngoài ra, $d(I,(P))=d(I,(Q)) \Leftrightarrow \dfrac{|2 a-b-2 c-2|}{\sqrt{2^{2}+(-1)^{2}+(-2)^{2}}}=\dfrac{|2 a-b-2 c+10|}{\sqrt{2^{2}+(-1)^{2}+(-2)^{2}}}$

$\Leftrightarrow|2 a-b-2 c-2|=|2 a-b-2 c+10| $

$\Leftrightarrow 2 a-b-2 c+4=0 .$

Do đó, $I$ luôn thuộc mặt phẳng $(R): 2 x-y-2 z+4$

Bước 3: Gọi $H$ là hình chiếu vuông góc của $A$ lên $(R)$.Tính HI và tính bán kính $r$

Gọi $H$ là hình chiếu vuông góc của $A$ lên $(R)$. Vì $A$,

Ta có $A H=d(A,(R))=\dfrac{|2.1-2-2.1+4|}{\sqrt{2^{2}+(-1)^{2}+(-2)^{2}}}=\dfrac{2}{3}$

Mà $A H \perp(R) \Rightarrow A H \perp H I$, do đó $\Delta A H I$ vuông tại $H$ nên

$H I=\sqrt{A I^{2}-A H^{2}}=\sqrt{2^{2}-\left(\dfrac{2}{3}\right)^{2}}=\dfrac{4 \sqrt{2}}{3}$

Vậy $I$ luôn thuộc đường tròn tâm $H$, nằm trên mặt phẳng $(R)$, bán kính $r=\dfrac{4 \sqrt{2}}{3}$

Bước 1: Tìm phương trình mặt phẳng \((AMN)\) và \((BCD)\)

Ta thấy \(M(2;1; - 3);N(4;3; - 6) \in \Delta \)

\( \Rightarrow \overrightarrow {AM} (1;2; - 2);\overrightarrow {AN} (3;4; - 5)\)\( \Rightarrow [\overrightarrow {AM} ;\overrightarrow {AN} ] = \overrightarrow {{n_1}}  = ( - 2; - 1; - 2)\)

\( \Rightarrow \) Mặt phẳng \((AMN)\) (hay \((ACD)\) ) đi qua điểm \(A(1; - 1; - 1)\) và nhận \(\overrightarrow {{n_1}} ( - 2; - 1;2)\) làm vectơ pháp tuyến có phương trình: \(2x + y + 2z + 1 = 0\).

Tương tự, ta có phương trình \((BCD):x + 2y + 2z + 2 = 0\).

Bước 2: Gọi tâm mặt cầu là \(I(m;0;0)(m > 0)\). Tính \(d(I;(BCD))\)

Gọi tâm mặt cầu là \(I(m;0;0)(m > 0)\).

Vì mặt cầu tiếp xúc với các mặt của tứ diện ABCD nên

\(d(I;(ACD)) = d(I;(BCD))\)\( \Leftrightarrow \dfrac{{|2m + 1|}}{3} = \dfrac{{|m + 2|}}{3}\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 1}\\{m =  - 1(L)}\end{array}} \right.\).

\( \Rightarrow I(1;0;0)\) và \(d(I;(BCD)) = 1.\)

Bước 3: Gọi \(C(2t + 2;2t + 1; - 3t - 3) \in \Delta \). Tìm phương trình mặt phẳng \((ABC)\)

Gọi \(C(2t + 2;2t + 1; - 3t - 3) \in \Delta \)

Ta có \(\overrightarrow {AB} ( - 3;0;2);\)\(\overrightarrow {AC} (2t + 1;2t + 2; - 3t - 2)\)

\( \Rightarrow [\overrightarrow {AB} ;\overrightarrow {AC} ] = \overrightarrow {{n_2}} \)\( = ( - 4t - 4; - 5t - 4; - 6t - 6)\)

\( \Rightarrow \) Mặt phẳng \((ABC)\) đi qua điểm \(A(1; - 1; - 1)\) và nhận \(\overrightarrow {{n_2}} ( - 4t - 4; - 5t - 4; - 6t - 6)\)

làm vectơ pháp tuyến có phương trình:

\((4t + 4)x + (5t + 4)y + (6t + 6)z\)\( + 7t + 6 = 0\).

Bước 4: Tính CD.

Vì mặt cầu tiếp xúc với các mặt của tứ diện ABCD nên

\(d(I;(ABC)) = d(I;(BCD)) = 1\)\( \Rightarrow \left[ {\begin{array}{*{20}{l}}{t =  - 1}\\{t =  - \dfrac{8}{{11}}}\end{array} \Rightarrow CD = \dfrac{{3\sqrt {17} }}{{11}}} \right.\)

Bước 1: Viết phương trình mặt phẳng trung trực của AB, BC, CD.

Ta có: \(\overrightarrow {AB}  = \left( { - 4; - 4;0} \right)\); \(\overrightarrow {BC}  = \left( {8;3; - 3} \right)\); \(\overrightarrow {CD}  = \left( { - 7; - 3; - 4} \right)\)

Trung điểm của AB là: M(-1;3;4)

Trung điểm của BC là: \(N\left( {1;\dfrac{5}{2};\dfrac{5}{2}} \right)\)

Trung điểm của AB là: \(P\left( {\dfrac{3}{2};\dfrac{5}{2}; - 1} \right)\)

Phương trình mặt phẳng trung trực của AB:

\(\left( {x + 1} \right) + \left( {y - 3} \right) = 0\) \( \Leftrightarrow x + y - 2 = 0\)

Phương trình mặt phẳng trung trực của BC:

\(\begin{array}{l}8\left( {x - 1} \right) + 3\left( {y - \dfrac{5}{2}} \right) - 3\left( {z - \dfrac{5}{2}} \right) = 0\\ \Leftrightarrow 8x + 3y - 3z - 8 = 0\end{array}\)

Phương trình mặt phẳng trung trực của CD:

\(\begin{array}{l}7\left( {x - \dfrac{3}{2}} \right) + 3\left( {y - \dfrac{5}{2}} \right) + 4\left( {z + 1} \right) = 0\\ \Leftrightarrow 7x + 3y + 4z - 14 = 0\end{array}\)

Bước 2: Khi đó giao điểm I của 3 mặt phẳng là tâm mặt cầu ngoại tiếp tứ diện ABCD, tìm bán kính IA.

Gọi I là giao điểm của 3 mặt phẳng trung trực vừa tìm được

Khi đó ta có tọa độ của I thỏa mãn hệ \(\left\{ \begin{array}{l}x + y - 2 = 0\\8x + 3y - 3z - 8 = 0\\7x + 3y + 4z - 14 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 1\\z = 1\end{array} \right.\)

=> \(I\left( {1;1;1} \right)\)

\( =  > IA = \sqrt {{0^2} + {4^2} + {3^2}}  = 5\)

Vậy bán kính đường tròn ngoại tiếp tứ diện ABCD bằng 5.

Mặt phẳng chứa trục hoành có dạng \(ay + bz = 0\,\,\left( P \right)\,\,\left( {{a^2} + {b^2} \ne 0} \right)\)

Mặt cầu (S) có tâm \(I\left( {2;2; - 1} \right)\), bán kính \(R = 2\).

Để (P) tiếp xúc với (S) thì \(d\left( {I,\left( P \right)} \right) = R \Leftrightarrow \dfrac{{\left| {2a - b} \right|}}{{\sqrt {{a^2} + {b^2}} }} = 2\)

\(\begin{array}{l} \Leftrightarrow 4{a^2} - 4ab + {b^2} = 4{a^2} + 4{b^2}\\ \Leftrightarrow 3{b^2} + 4ab = 0 \Leftrightarrow \left[ \begin{array}{l}b = 0\\b =  - \dfrac{{4a}}{3}\end{array} \right.\end{array}\)

Trường hợp \(b = 0\) loại do không có đáp án nào thỏa mãn.

Trường hợp \(b =  - \dfrac{{4a}}{3}\). Chọn \(a = 3 \Rightarrow b =  - 4\).

Vậy phương trình mặt phẳng cần tìm là: \(3y - 4z = 0\).