Phương trình tiếp tuyến của đồ thị \(y=\frac{2x-1}{x-1}\) tại điểm \(A\left( 2;3 \right)\) là:
\(y'=\frac{-1}{{{\left( x-1 \right)}^{2}}}\Rightarrow y'\left( 2 \right)=\frac{-1}{{{\left( 2-1 \right)}^{2}}}=-1\Rightarrow \) Phương trình tiếp tuyến của đồ thị hàm số \(y=\frac{2x-1}{x-1}\) tại \( A\left( 2;3 \right)\) là:
\(y=-\left( x-2 \right)+3=-x+5\) .
Cho hàm số \(y = \dfrac{1}{4}{x^4} - 2{x^2} + 2\). Hỏi đồ thị hàm số đã cho có bao nhiêu tiếp tuyến song song với trục hoành?
Ta có : \(y' = {x^3} - 4x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = 2\\x = 2 \Rightarrow y = - 2\\x = - 2 \Rightarrow y = - 2\end{array} \right.\)
Phương trình tiếp tuyến tại điểm \(\left( {0;2} \right)\) có phương trình \(y = 0\left( {x - 0} \right) + 2 \Leftrightarrow y = 2\).
Phương trình tiếp tuyến tại điểm \(\left( {2; - 2} \right)\) có phương trình \(y = 0\left( {x - 2} \right) - 2 \Leftrightarrow y = - 2\).
Phương trình tiếp tuyến tại điểm \(\left( { - 2; - 2} \right)\) có phương trình \(y = 0\left( {x + 2} \right) - 2 \Leftrightarrow y = - 2\).
Vậy có hai tiếp tuyến cần tìm là \(y = 2\) và \(y = - 2\).
Viết phương trình tiếp tuyến của đồ thị hàm số \(y=\frac{4}{x-1}\)tại điểm có hoành độ \(x=-1.\)
\(\begin{array}{l}y = \frac{4}{{x - 1}} \Rightarrow y' = - \frac{4}{{{{(x - 1)}^2}}}\\y(1) = \frac{4}{{ - 1 - 1}} = - 2;\,\,\,y'( - 1) = - \frac{4}{{{{( - 1 - 1)}^2}}} = - 1\end{array}\)
Phương trình tiếp tuyến cần tìm: \(y=y'(-1)(x+1)+y(1)\Leftrightarrow y=-1.\left( x+1 \right)-2\Leftrightarrow y=-x-3\)
Cho hàm số \(y={{x}^{3}}+{{x}^{2}}-5x+1\). Viết phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ x = 2.
Ta có: \(y'=3{{x}^{2}}+2x-5\Rightarrow y'\left( 2 \right)=11;\,\,y\left( 2 \right)=3\)
\(\Rightarrow \) Phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ x = 2 là: \(y=11\left( x-2 \right)+3=11x-19\).
Phương trình tiếp tuyến của đồ thị hàm số \(y=x+\sqrt{{{x}^{2}}+1}\) tại điểm có hoành độ \(x=0\) là :
TXĐ: D = R.
Ta có \(y'=1+\frac{x}{\sqrt{{{x}^{2}}+1}}\Rightarrow y'\left( 0 \right)=1;\,\,y\left( 0 \right)=1\)
\(\Rightarrow \) Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ \(x=0\) là:
\(y=y'\left( 0 \right)\left( x-0 \right)+y\left( 0 \right)=1\left( x-0 \right)+1=x+1\)
Cho hàm số \(y = \dfrac{5}{3}{x^3} - {x^2} + 4\) có đồ thị \((C)\). Tiếp tuyến của \((C)\) tại điểm có hoành độ \({x_0} = 3\) có hệ số góc là:
\(y = \dfrac{5}{3}{x^3} - {x^2} + 4 \Rightarrow y' = 5{x^2} - 2x\)
\(y'(3) = {5.3^2} - 2.3 = 39\)
Cho hàm số \(y={{x}^{3}}-3{{x}^{2}}-2\). Hệ số góc của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ \(x=2\) là:
Ta có \({y}'=3{{x}^{2}}-6x\Rightarrow {y}'\left( 2 \right)={{3.2}^{2}}-6.2=0\) nên hệ số góc cần tìm là \(k=0\).
Tiếp tuyến của đồ thị hàm số \(f\left( x \right)=\frac{1}{3}{{x}^{3}}-\frac{1}{2}{{x}^{2}}-4x+6\) tại điểm có hoành độ là nghiệm của phương trình \({f}''\left( x \right)=0\) có hệ số góc bằng
Ta có \({f}'\left( x \right)={{x}^{2}}-x-4\Rightarrow \,\,{f}''\left( x \right)=2x-1=0\Leftrightarrow \,\,x=\frac{1}{2}.\)
Suy ra hệ số góc cần tìm là \(k={f}'\left( \frac{1}{2} \right)=-\frac{17}{4}.\)
Cho hàm số \(y = {x^4} - 1\) có đồ thị \(\left( C \right)\). Tiếp tuyến của đồ thị \(\left( C \right)\) tại điểm với hoành độ bằng 0 có hệ số góc là
\(y = {x^4} - 1 \Rightarrow y' = 4{x^3} \Rightarrow y'\left( 0 \right) = 0 \Rightarrow \) Tiếp tuyến của đồ thị \(\left( C \right)\) tại điểm với hoành độ bằng 0 có hệ số góc là 0.
Cho hàm số \(y = {x^3} - 3x + 2\) có đồ thị \((C)\). Hỏi có bao nhiêu điểm trên đường thẳng \(y = 9x - 14\) sao cho từ đó kẻ được hai tiếp tuyến đến \((C)\) ?
Bước 1: Tham số hóa điểm M. Gọi \(\Delta \) là đường thẳng đi qua \(M\) và có hệ số góc k.
Gọi M là một điểm thuộc d \( \Rightarrow M(a;9a - 14)\).
Gọi \(\Delta \) là đường thẳng đi qua \(M\) và có hệ số góc \(k\)\( \Rightarrow \) \(\Delta :y = k(x - a) + 9a - 14\).
Bước 2: Lập hệ từ điều kiện \(\Delta \) tiếp xúc \((C)\) và giải.
\(\Delta \) tiếp xúc \((C)\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{k = 3{x^2} - 3(1)}\\{{x^3} - 3x + 2 = k(x - a) + 9a - 14(2)}\end{array}} \right.\)
Thay (1) vào (2) ta có:
\({x^3} - 3x + 2\)\( = \left( {3{x^2} - 3} \right)(x - a) + 9a - 14\)
\( \Leftrightarrow 2{x^3} - 3a{x^2} + 12a - 16 = 0\)
\( \Leftrightarrow (x - 2)\)\(\left[ {2{x^2} + (4 - 3a)x + 8 - 6a} \right] = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 2}\\{2{x^2} + (4 - 3a)x + 8 - 6a = 0(3)}\end{array}} \right.\)
Bước 3: Lập luận để từ \(M\) kẻ được hai tiếp tuyến
Để từ \(M\) kẻ được hai tiếp tuyến thì (3) phải có nghiệm kép khác 2 hoặc (3) phải có hai nghiệm phân biệt, trong đó có một nghiệm \(x = 2\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{{\Delta _{(3)}} = 9{a^2} + 24a - 48 = 0}\\{8 + (4 - 3a)2 + 8 - 6a \ne 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{l}}{{\Delta _{(3)}} = 9{a^2} + 24a - 48 > 0}\\{8 + (4 - 3a)2 + 8 - 6a = 0}\end{array}} \right.}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{\left[ \begin{array}{l}a = \dfrac{4}{3}\\a = - 4\end{array} \right.}\\{a \ne 2}\end{array}} \right.\\\left\{ \begin{array}{l}a < - 4 \cup a > \dfrac{4}{3}\\a = 2\end{array} \right.\end{array}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{a = \dfrac{4}{3}}\\{a = - 4}\\{a = 2}\end{array}} \right.\)
Vậy có ba điểm thỏa mãn bài toán.
Tiếp tuyến của đồ thị hàm số \(y = \dfrac{{2x - 3}}{{2 - x}}\) tại điểm có hoành độ \(x = - 1\) có hệ số góc bằng bao nhiêu?
TXĐ \(D = \mathbb{R}\backslash \left\{ 2 \right\}\).
Ta có \(y = \dfrac{{2x - 3}}{{2 - x}} = \dfrac{{2x - 3}}{{ - x + 2}} \Rightarrow y' = \dfrac{1}{{{{\left( {2 - x} \right)}^2}}}\).
Vậy hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm có hoành độ \(x = - 1\) là \(k = y'\left( { - 1} \right) = \dfrac{1}{9}\).
Hệ số góc của tiếp tuyến của đồ thị hàm số $y = \dfrac{{{x^4}}}{4} + \dfrac{{{x^2}}}{2} - 1$ tại điểm có hoành độ $x = - 1$ là:
Ta có $y' = {x^3} + x$
$ \Rightarrow $ Hệ số góc của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ $x=-1$ là $k = y'( - 1) = - 2$
Viết phương trình tiếp tuyến của đồ thị hàm số $y = - 2{x^3} + 4x + 2$ tại điểm có hoành độ bằng $0.$
Bước 1: Gọi tiếp điểm của tiếp tuyến với đồ thị hàm số là $A\left( {0;2} \right).$
Bước 2: Phương trình tiếp tuyến tại điểm A có dạng $y = y'\left( 0 \right)\left( {x - 0} \right) + 2.$
Ta có $y' = - 6{x^2} + 4 \Rightarrow y'\left( 0 \right) = 4.$ Do đó phương trình tiếp tuyến là $y = 4x + 2.$
Viết phương trình tiếp tuyến của đồ thị hàm số $y = - {x^4} + 6{x^2} - 5$ tại điểm cực tiểu của nó.
Ta có: $y' = - 4{{\text{x}}^3} + 12{\text{x}}$$ \Rightarrow y' = 0 \Leftrightarrow x = 0$ hoặc $x = \sqrt 3 $ hoặc $x = - \sqrt 3 $
Ta có bảng biến thiên
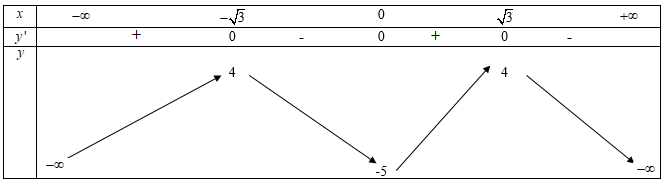
Quan sát bảng biến thiên ta thấy tiếp điểm là $(0;-5)$ và $y'(0)=0$.
Vậy phương trình đường tiếp tuyến tại điểm cực tiểu của đồ thị hàm số là $y = - 5$
Có bao nhiêu tiếp tuyến với đồ thị $\left( C \right):y = {x^4} - 2{x^2}$ đi qua gốc tọa độ $O$?
Giả sử $\left( {{x_0};{y_0}} \right)$ là điểm thuộc đồ thị hàm số $\left( C \right)$ có tiếp tuyến đi qua gốc tọa độ $O$
Ta có: $y' = 4{{\text{x}}^3} - 4{\text{x}}$
Ta có phương trình đường thẳng tiếp tuyến tại điểm $\left( {{x_0};{y_0}} \right)$
$y = \left( {4{\text{x}}_0^3 - 4{{\text{x}}_0}} \right)\left( {x - {x_0}} \right) + {y_0}$$ \Leftrightarrow y = \left( {4{\text{x}}_0^3 - 4{{\text{x}}_0}} \right)\left( {x - {x_0}} \right) + {x_0}^4 - 2x_0^2$
Thay $\left( {0;0} \right)$ vào phương trình trên ta được:
\(\begin{array}{l}0 = \left( {4{\rm{x}}_0^3 - 4{{\rm{x}}_0}} \right)\left( {0 - {x_0}} \right) + {x_0}^4 - 2x_0^2\\ \Leftrightarrow - 3x_0^4 + 2x_0^2 = 0 \Leftrightarrow x_0^2\left( { - 3x_0^2 + 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x_0} = 0\\{x_0} = \pm \sqrt {\dfrac{2}{3}} \end{array} \right.\end{array}\)
Vậy có ba điểm có tiếp tuyến đi qua gốc tọa độ.
Tiếp tuyến của đồ thị hàm số $y = \dfrac{{{x^3}}}{3} - 2{x^2} + x + 2$ song song với đường thẳng $y = - 2x + 5$ có phương trình là:
Tiếp tuyến $(d)$ song song với đường thẳng $y = - 2x + 5$ nên có hệ số góc .
Suy ra $y' = - 2$ hay ${x^2} - 4x + 1 = - 2 \Leftrightarrow \left( {x - 1} \right)\left( {x - 3} \right) = 0$ $ \Rightarrow \left[ \begin{gathered}x = 1,y = \dfrac{4}{3} \hfill \\x = 3,y = - 4 \hfill \\ \end{gathered} \right.$
Với $x = 1;y = \dfrac{4}{3}$ thì ${d_1}:y = - 2\left( {x - 1} \right) + \dfrac{4}{3}$ hay ${d_1}:y = - 2x + \dfrac{{10}}{3}$
Với $x = 3;y = - 4$ thì ${d_2}:y = - 2\left( {x - 3} \right) - 4$ hay ${d_2}:y = - 2x + 2$
Giả sử tiếp tuyến của đồ thị hàm số $y = 2{x^3} - 6{x^2} + 18x + 1$ song song với đường thẳng $d:12x - y = 0$ có dạng $y = ax + b$. Khi đó tổng $a + b$ là:
Ta có: $y' = 6{{\text{x}}^2} - 12{\text{x}} + 18$
Tiếp tuyến của đồ thị hàm số tại điểm $\left( {{x_0};{y_0}} \right)$ có hệ số góc $k = y'\left( {{x_0}} \right)$
Do tiếp tuyến song song với đường thẳng $y = 12x$ nên:
$k = 12 \Leftrightarrow 6x_0^2 - 12{x_0} + 18 = 12 \Leftrightarrow {\left( {{x_0} - 1} \right)^2} = 0 \Leftrightarrow {x_0} = 1 \Rightarrow {y_0} = 15$$ \Rightarrow y = 12\left( {x - 1} \right) + 15 \Rightarrow y = 12x + 3$
Vậy $a = 12,b = 3 \Rightarrow a + b = 15$
Đồ thị hàm số nào sau đây có tiếp tuyến tại giao điểm của đồ thị và trục tung có hệ số góc âm?
Đối với hàm số $y = \dfrac{{5x + 1}}{{x + 1}}$thì $y' = \dfrac{4}{{{{\left( {x + 1} \right)}^2}}} > 0,\forall x \ne - 1$
⇒ Hệ số góc của tiếp tuyến luôn dương.
Đối với hàm số: $y = \dfrac{{2x + 1}}{{x + 1}}$ thì $y' = \dfrac{1}{{{{\left( {x + 1} \right)}^2}}} > 0,\forall x \ne - 1$
⇒ Hệ số góc của tiếp tuyến luôn dương.
Đối với hàm số $y = \dfrac{1}{3}{x^3} + {x^2} + 4x + 1 = > y' = {x^2} + 2x + 4 = {(x + 1)^2} + 3 > 0,\forall x$
⇒ Hệ số góc của tiếp tuyến luôn dương.
Xét hàm số $y = \dfrac{1}{{x + 1}}$: Có giao điểm của đồ thị hàm số với trục tung là: $A(0;1)$
Có $y' = \dfrac{{ - 1}}{{{{\left( {x + 1} \right)}^2}}} < 0\,\forall x \ne 1 \Rightarrow y'\left( 0 \right) < 0$
⇒ Hệ số góc của tiếp tuyến tại $A$ có hệ số âm.
Cho hàm số $y = {x^3} - 3{x^2} + 5x - 2$ có đồ thị $(C)$. Viết phương trình tiếp tuyến của đồ thị $(C)$ có hệ số góc nhỏ nhất.
Xét hàm số: $y = {x^3} - 3{x^2} + 5x - 2$ trên $R$
Có $y' = 3{x^2} - 6x + 5 = 3{\left( {x - 1} \right)^2} + 2 \geqslant 2.$
Dấu “=” xảy ra $x = 1.$
Với $x = 1 \Rightarrow y = 1.$
Vậy đường thẳng cần tìm là: $y - 1 = 2\left( {x - 1} \right) \Leftrightarrow y = 2x - 1.$
Cho hàm số: $y={{x}^{3}}-{{x}^{2}}+1$ . Tìm điểm nằm trên đồ thị hàm số sao cho tiếp tuyến tại điểm đó có hệ số góc nhỏ nhất.
Giả sử $M(a;b)$ là điểm thuộc đồ thị hàm sao cho tiếp tuyến $\left( \Delta \right)$ tại đó có hệ số góc nhỏ nhất là $k$.
\( \Rightarrow \left( \Delta \right):y = y'\left( a \right).(x - a) + b\)
Do \({k_{\min }} \Rightarrow \left( {3{a^2} - 2a} \right)\min \)
Xét \(3\left( {{a^2} - 2.\dfrac{1}{3}a + \dfrac{1}{9}} \right) = 3{\left( {a - \dfrac{1}{3}} \right)^2} \ge 0 \Leftrightarrow 3{a^2} - 2a + \dfrac{1}{3} \ge 0 \Leftrightarrow 3{a^2} - 2a \ge \dfrac{{ - 1}}{3}\)
\( \Rightarrow k = - \dfrac{1}{3}\)khi \(a = \dfrac{1}{3} \Rightarrow b = \dfrac{{25}}{{27}}\)

