Trong không gian với hệ trục tọa độ \(Oxyz,\) cho vật thể \(\left( H \right)\) giới hạn bởi hai mặt phẳng có phương trình \(x = a\) và \(x = b\)\(\left( {a < b} \right)\). Gọi \(S\left( x \right)\) là diện tích thiết diện của \(\left( H \right)\) bị cắt bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ là \(x,\) với \(a \le x \le b\). Giả sử hàm số \(y = S\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right].\) Khi đó, thể tích \(V\) của vật thể \(\left( H \right)\) được cho bởi công thức:
Trong không gian với hệ trục tọa độ \(Oxyz,\) cho vật thể \(\left( H \right)\) giới hạn bởi hai mặt phẳng có phương trình \(x = a\) và \(x = b\)\(\left( {a < b} \right)\). Gọi \(S\left( x \right)\) là diện tích thiết diện của \(\left( H \right)\) bị cắt bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ là \(x,\) với \(a \le x \le b\). Giả sử hàm số \(y = S\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right].\) Khi đó, thể tích \(V\) của vật thể \(\left( H \right)\) được cho bởi công thức: \(V = \int\limits_a^b {S\left( x \right){\rm{d}}x} .\).
Tính thể tích của vật thể nằm giữa hai mặt phẳng x =1 và x = 2 , biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x , (1 ≤ x ≤ 2) là một hình chữ nhật có độ dài hai cạnh là \(x\) và \(\sqrt {{x^2} + 3} \).
Diện tích mặt cắt là: \(S\left( x \right) = x\sqrt {{x^2} + 3} \)
Thể tích của vật thể đó là: \(V = \int\limits_1^2 {S\left( x \right)} \,dx = \int\limits_1^2 {x\sqrt {{x^2} + 3} } \,dx\).
Đặt \(t = \sqrt {{x^2} + 3} \)\( \Rightarrow {t^2} = {x^2} + 3 \Rightarrow tdt = xdx\).
Đổi cận: \(\left\{ \begin{array}{l}x = 1 \Rightarrow t = 2\\x = 2 \Rightarrow t = \sqrt 7 \end{array} \right.\).
\( \Rightarrow V = \int\limits_2^{\sqrt 7 } {t.tdt} = \left. {\dfrac{{{t^3}}}{3}} \right|_2^{\sqrt 7 } = \dfrac{{7\sqrt 7 - 8}}{3}.\)
Cho hình \(\left( H \right)\) giới hạn bởi đồ thị hàm số \(y = {x^3}\), trục hoành và hai đường thẳng \(x = 0,x = 1\). Thể tích khối tròn xoay tạo thành khi quay \(\left( H \right)\) quanh trục \(Ox\) được tính bởi:
Thể tích vật thể là: \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} = \pi \int\limits_0^1 {{{\left( {{x^3}} \right)}^2}dx} = \pi \int\limits_0^1 {{x^6}dx} \)
Cho hình \(\left( H \right)\) giới hạn bởi đồ thị hàm số \(x = f\left( y \right)\) , trục tung và hai đường thẳng \(y = a,y = b\). Thể tích khối tròn xoay tạo thành khi quay \(\left( H \right)\) quanh trục \(Oy\) là:
Công thức tính thể tích khối tròn xoay tạo thành khi quay hình phẳng \(\left( H \right)\) giới hạn bởi đồ thị hàm số \(x = f\left( y \right)\), trục \(Oy\) và hai đường thẳng \(y = a,y = b\left( {a < b} \right)\) quanh trục \(Oy\) là: \(V = \pi \int\limits_a^b {{f^2}\left( y \right)dy} \)
Cho hình \(\left( H \right)\) giới hạn bởi đường cong \({y^2} + x = 0\), trục \(Oy\) và hai đường thẳng \(y = 0,y = 1\). Thể tích khối tròn xoay tạo thành khi quay \(\left( H \right)\) quanh trục \(Oy\) được tính bởi:
Ta có: \({y^2} + x = 0 \Leftrightarrow x = - {y^2}\)
Vậy thể tích khối tròn xoay đó là: \(V = \pi \int\limits_a^b {{f^2}\left( y \right)dy} = \pi \int\limits_0^1 {{{\left( { - {y^2}} \right)}^2}dy} = \pi \int\limits_0^1 {{y^4}dy} \)
Cho hình phẳng $\left( H \right)$ giới hạn bởi \(y = \dfrac{1}{3}{x^3} - {x^2}\) và $Ox$. Thể tích khối tròn xoay sinh ra khi quay $\left( H \right)$ quanh $Ox$ bằng :
Ta có \(\dfrac{1}{3}{x^3} - {x^2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 3\end{array} \right.\)
$V=\pi {{\int\limits_{0}^{3}{\left( \dfrac{1}{3}{{x}^{3}}-{{x}^{2}} \right)}}^{2}}d\text{x }=\pi \int\limits_{0}^{3}{\left( \dfrac{1}{9}{{x}^{6}}-\dfrac{2}{3}{{x}^{5}}+{{x}^{4}} \right)}dx$
$=\left. \pi \left( \dfrac{1}{63}{{x}^{7}}-\dfrac{1}{9}{{x}^{6}}+\dfrac{1}{5}{{x}^{5}} \right) \right|_{0}^{3}=\dfrac{81}{35}\pi $
Kí hiệu $\left( H \right)$ là hình phẳng giới hạn bởi đồ thị hàm số $y = 2\left( {x-1} \right){e^x}$, trục tung và trục hoành. Tính thể tích $V$ của khối tròn xoay thu được khi quay hình $\left( H \right)$ xung quanh trục $Ox$ .
Xét giao điểm $2\left( {x - 1} \right){e^x} = 0 \Leftrightarrow x = 1$
Thể tích cần tính: $V = \pi \int\limits_0^1 {{{\left[ {2\left( {x - 1} \right){e^x}} \right]}^2}dx} = 4\pi \int\limits_0^1 {{{\left( {x - 1} \right)}^2}{e^{2x}}dx} = \pi \left( {{e^2} - 5} \right)$ (dùng máy tính thử)
Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường \(y = {x^2} + 1;x = 0\) và tiếp tuyến của đồ thị hàm số \(y = {x^2} + 1\) tại điểm \(A\left( {1;2} \right)\) quanh trục $Ox$ là
$y' = 2x;y'\left( 1 \right) = 2$ suy ra phương trình tiếp tuyến là $y = 2\left( {x - 1} \right) + 2 = 2x$
Ta có: $x^2+1=2x \Leftrightarrow x=1$.
Trong đoạn $[0;1]$ thì $x^2+1\ge 2x$ nên:
Thể tích khối tròn xoay $V = \pi \int\limits_0^1 {\left[ {{{\left( {x^2 + 1} \right)}^2} - {{\left( {2x} \right)}^2}} \right]} dx = \pi \int\limits_0^1 {\left( {{x^4} - 2{{\rm{x}}^2} +1} \right)} dx = \dfrac{8}{{15}}\pi $
Gọi $V$ là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y = \sqrt x ,y = 0\) và $x = 4$ quanh trục $Ox$ . Đường thẳng \(x = a(0 < a < 4)\) cắt đồ thị hàm số \(y = \sqrt x \) tại $M$ (hình vẽ bên).
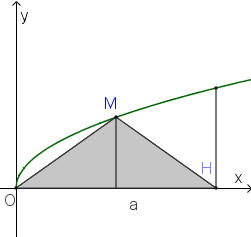
Gọi ${V_1}$ là thể tích khối tròn tạo thành khi quay quanh tam giác $OMH$ quanh trục $Ox$. Biết rằng \(V = 2{V_1}\) . Khi đó:
Thể tích khối tròn xoay $V = \pi \int\limits_0^4 {xdx = \pi \left. {\dfrac{{{x^2}}}{2}} \right|_0^4} = 8\pi $
Suy ra ${V_1} = 4\pi $
Gọi $N$ là giao điểm của đường thẳng $x=a$ và trục hoành. Khi đó ${V_1}$ là thể tích tạo được khi xoay hai tam giác $OMN$ và $MNH$ quanh trục $Ox$ với $N$ là hình chiếu của $M$ trên $OH$.
Ta có ${V_1} = \dfrac{1}{3}\pi .a.{\left( {\sqrt a } \right)^2} + \dfrac{1}{3}\pi .\left( {4 - a} \right).{\left( {\sqrt a } \right)^2} = \dfrac{4}{3}\pi a$
Suy ra $\dfrac{4}{3}\pi a = 4\pi \Rightarrow a = 3$
Cho hai hàm số \(y = {f_1}\left( x \right)\) và \(y = {f_2}\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và có đồ thị như hình vẽ bên. Gọi $S$ là hình phẳng giới hạn bởi hai đồ thị trên và các đường thẳng \(x = a,x = b\). Thể tích $V$ của vật thể tròn xoay tạo thành khi quay $S$ quanh trục $Ox$ được tính bởi công thức nào sau đây ?
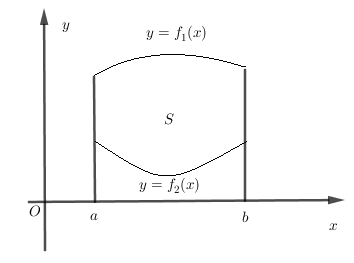
Theo công thức trên ta có: \(V = \pi \int\limits_a^b {\left( {f_1^2(x) - f_2^2\left( x \right)} \right)} dx\) (vì đồ thị hàm số \(y = {f_1}\left( x \right)\) nằm phía trên đồ thị hàm số \(y = {f_2}\left( x \right)\).
Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường $y = \sqrt {2 - x} ;y = x$ xung quanh trục $Ox$ được tính theo công thức nào sau đây?
Thể tích khối tròn xoay cần tìm là thể tích khối tròn xoay khi quay 2 hình phẳng $(H_1)$ và $(H_2)$ quanh trục $Ox$ trong đó $(H_1)$ giới hạn bởi đường thẳng $y = x; x = 0; x = 1$ và $(H_2)$ được giới hạn bởi các đường $y = \sqrt {2 - x} ;x = 1;x = 2$.
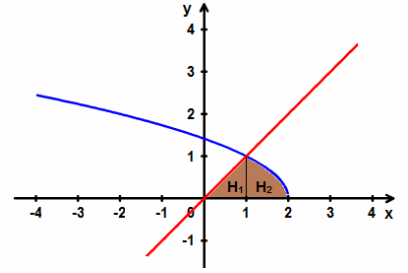
Khi đó ta có:
Thể tích $V$ cần tính chính bằng thể tích $V_1$ của khối tròn xoay thu được khi quay hình $(H_1)$ xung quanh trục $Ox$ cộng với thể tích $V_2$ của khối tròn xoay thu được khi quay hình $(H_2)$ xung quanh trục $Ox:$
$V = \pi \int\limits_0^1 {{x^2}dx} + \pi \int\limits_1^2 {(2 - x)dx} $
Cho vật thể \(V\) được giới hạn bởi hai mặt phẳng \(x = a\) và \(x = b\left( {a < b} \right)\), mặt phẳng vuông góc với trục \(Ox\) cắt \(V\) theo thiết diện \(S\left( x \right)\). Thể tích của \(V\) được tính bởi:
Tính thể tích của vật thể giới hạn bởi các mặt phẳng \(x = a,x = b\) biết diện tích thiết diện cắt bởi mặt phẳng vuông góc trục $Ox$ là \(S = S\left( x \right)\).
Công thức tính: \(V = \int\limits_a^b {S\left( x \right)dx} \).
Cho vật thể \(V\) được giới hạn bởi hai mặt phẳng \(x = 0\) và \(x = - 2\), mặt phẳng vuông góc với trục \(Ox\) cắt \(V\) theo thiết diện \(S\left( x \right) = 2{x^2}\). Thể tích của \(V\) được tính bởi:
Thể tích vật thể là: \(V = \int\limits_a^b {S\left( x \right)dx} = \int\limits_{ - 2}^0 {2{x^2}dx} \)
Tính thể tích $V$ của phần vật thể giới hạn bởi hai mặt phẳng \(x = 1\) và \(x = 3\), biết rằng khi cắt vật thể bởi mặt phẳng vuông góc với trục $Ox$ tại điểm có hoành độ \(x\) (\(1 \le x \le 3\)) thì được thiết diện là một hình chữ nhật có độ dài hai cạnh là \(3x\) và \(\sqrt {3{x^2} - 2} \).
Diện tích mỗi mặt thiết diện sẽ là :\(S\left( x \right) = 3x\sqrt {3{x^2} - 2} \) \(V = \int_1^3 {3x\sqrt {3{x^2} - 2} dx} = \dfrac{{124}}{3}\)
Cho hình phẳng giới hạn bởi $D = \left\{ {y = \tan x;\,\,y = 0;\,\,x = 0;\,\,x = \dfrac{\pi }{3}} \right\}.$ Thể tích vật tròn xoay khi $D$ quay quanh trục $Ox$ là $V = \pi \left( {a - \dfrac{\pi }{b}} \right),$ với $a,\,\,b \in R.$ Tính $T = {a^2} + 2b.$
Thể tích vật tròn xoay cần tính là $V = \pi \int\limits_0^{\dfrac{\pi }{3}} {{{\tan }^2}x\,{\rm{d}}x} = \pi \int\limits_0^{\dfrac{\pi }{3}} {\left( {\dfrac{1}{{{{\cos }^2}x}} - 1} \right)\,{\rm{d}}x} .$$=\pi \left. \left( \tan x-x \right) \right|_{0}^{\dfrac{\pi }{3}}=\pi \left( \sqrt{3}-\dfrac{\pi }{3} \right)=\pi \left( a-\dfrac{\pi}{3} \right)\,\,\xrightarrow{{}}\,\,\left\{ \begin{align} & a=\sqrt{3} \\ & b=3 \\ \end{align} \right..$
Vậy $T = {\left( {\sqrt 3 } \right)^2} + 2.3 = 9.$
Tính thể tích khi $S = \left\{ {y = {x^2} - 4x + 6;\,\,y = - \,{x^2} - 2x + 6} \right\}$ quay quanh trục $Ox.$
Hoành độ giao điểm của hai parabol là ${x^2} - 4x + 6 = - \,{x^2} - 2x + 6 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right..$
Trong khoảng $(0;1)$ thì ${12{x^3} - 36{x^2} + 24x}>0$ nên:
Thể tích vật tròn xoay cần tính là $V = \pi \int\limits_0^1 {\left| {{{\left( {{x^2} - 4x + 6} \right)}^2} - {{\left( { - \,{x^2} - 2x + 6} \right)}^2}} \right|{\rm{d}}x} $
$ = \pi \int\limits_0^1 {\left( {12{x^3} - 36{x^2} + 24x} \right){\rm{d}}x} = \pi \left. {\left( {3{x^4} - 12{x^3} + 12{x^2}} \right)} \right|_0^1 = 3\pi .$
Thể tích khối tròn xoay sinh ra bởi phép quay xung quanh $Ox$ của hình giới hạn bởi trục $Ox$ và parabol $\left( P \right):y = {x^2} - ax\,\,\,\,\left( {a > 0} \right)$ bằng $V = 2.$ Khẳng định nào dưới đây đúng ?
Phương trình hoành độ giao điểm của $\left( P \right)$ và $Ox$ là ${x^2} - ax = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = a\end{array} \right..$
Khi đó, thể tích cần xác định cho bởi $V = \pi \int\limits_0^a {{{\left( {{x^2} - ax} \right)}^2}{\rm{d}}x} = \pi \int\limits_0^a {\left( {{x^4} - 2a{x^3} + {a^2}{x^2}} \right){\rm{d}}x} $
$ = \pi \left. {\left( {\dfrac{{{x^5}}}{5} - \dfrac{{a{x^4}}}{2} + \dfrac{{{a^2}{x^3}}}{3}} \right)} \right|_0^a = \dfrac{{\pi {a^5}}}{{30}}.$
Mặt khác $V = 2 \Rightarrow \dfrac{{\pi {a^5}}}{{30}} = 2 \Leftrightarrow a = \sqrt[5]{{\dfrac{{60}}{\pi }}} \in \left( {\dfrac{3}{2};2} \right).$
Cho hình phẳng $\left( H \right)$ giới hạn bởi các đường $y = - \,{x^2} + 2x$ và $y = 0$. Tính thể tích của khối tròn xoay tạo thành khi quay hình $\left( H \right)$ quanh trục $Oy$ là
Ta có $y = - \,{x^2} + 2x \Rightarrow {\left( {x - 1} \right)^2} = 1 - y \Rightarrow \left[ \begin{array}{l}{\rm{ }}x = 1 - \sqrt {1 - y} \\{\rm{ }}x = 1 + \sqrt {1 - y} \end{array} \right..$
Xét phương trình tung độ giao điểm \(1 - \sqrt {1 - y} = 1 + \sqrt {1 - y} \Leftrightarrow \sqrt {1 - y} = 0 \Leftrightarrow y = 1\).
Khi đó, thể tích cần tính là $V = \pi \int\limits_0^1 {\left| {{{\left( {1 + \sqrt {1 - y} } \right)}^2} - {{\left( {1 - \sqrt {1 - y} } \right)}^2}} \right|{\rm{d}}y} = \left| {\pi \int\limits_0^1 {4\sqrt {1 - y} \,{\rm{d}}y} } \right|$
Đặt \(\sqrt {1 - y} = t \Leftrightarrow 1 - y = {t^2} \Leftrightarrow dy = - 2tdt\)
Đổi cận: \(\left\{ \begin{array}{l}y = 0 \Leftrightarrow t = 1\\y = 1 \Leftrightarrow t = 0\end{array} \right.\)
Khi đó $V=\left| -\pi \int\limits_{1}^{0}{4t.2tdt} \right|=\left| 8\pi \int\limits_{0}^{1}{{{t}^{2}}dt} \right|=\left| 8\left. \pi \dfrac{{{t}^{3}}}{3} \right|_{0}^{1} \right|=\dfrac{8\pi }{3}$
Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi đường \(\left( E \right):\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{9} = 1\) quay quanh \(Oy\,\,?\)
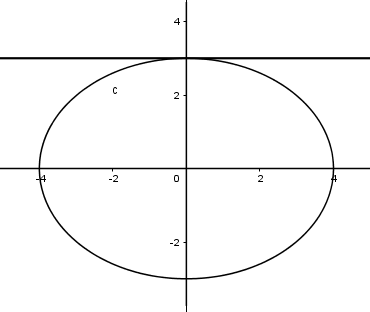
\(\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{9} = 1 \Leftrightarrow {x^2} = 16\left( {1 - \dfrac{{{y^2}}}{9}} \right) \Leftrightarrow x = \pm \dfrac{4}{3}\sqrt {9 - {y^2}} \)
Phương trình tung độ giao điểm của đồ thị \(\left( E \right)\) với $Oy$ là \(\dfrac{0}{{16}} + \dfrac{{{y^2}}}{9} = 1 \Leftrightarrow \left[ \begin{array}{l}y = - \,3\\y = 3\end{array} \right..\)
Ta xét thể tích vật tròn xoay khi xoay hình phẳng giới hạn bởi đồ thị hàm số \(x = \dfrac{4}{3}\sqrt {9 - {y^2}} \), đường thẳng $x = 0, y = 3, y = 0$ quanh trục $Oy$ là: \(V = \left| {\dfrac{{16}}{9}\pi \int\limits_0^3 {\left( {9 - {y^2}} \right)dy} } \right| = \left| {\dfrac{{16}}{9}\left. {\pi \left( {9y - \dfrac{{{y^3}}}{3}} \right)} \right|_0^3} \right| = 32\pi \).
Khi đó thể tích cần tìm là \(2V = 64\pi \).
Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đồ thị $y = - \,\sqrt {4 - {x^2}} ,\,\,{x^2} + 3y = 0$ quay quanh trục $Ox$ là $V = \dfrac{{a\pi \sqrt 3 }}{b},$ với $a,\,\,b > 0$ và $\dfrac{a}{b}$ là phân số tối giản. Tính tổng $T = a + b.$
\({x^2} + 3y = 0 \Leftrightarrow y = - \dfrac{{{x^2}}}{3}\)
Hoành độ giao điểm là nghiệm của phương trình
$ - \,\sqrt {4 - {x^2}} = - \dfrac{{{x^2}}}{3} \Leftrightarrow 3\sqrt {4 - {x^2}} = {x^2} \Leftrightarrow\left\{ \begin{array}{l}0 \le {x^2} \le 4\\{x^4} + 9{x^2} - 36 = 0\end{array} \right. $
$\Leftrightarrow {x^2} = 3 \Leftrightarrow x = \pm \,\sqrt 3 .$
Khi đó, thể tích khối tròn xoay cần tính là $V = \pi \int\limits_{ - \,\sqrt 3 }^{\sqrt 3 } {\left| {{{\left( { - \,\sqrt {4 - {x^2}} } \right)}^2} - {{\left( { - \,\dfrac{{{x^2}}}{3}} \right)}^2}} \right|\,{\rm{d}}x.} $
$ = \pi \int\limits_{ - \,\sqrt 3 }^{\sqrt 3 } {\left| {\left( {4 - {x^2}} \right) - \dfrac{{{x^4}}}{9}} \right|{\rm{d}}x} = \left| {\pi \left. {\left( {4x - \dfrac{{{x^3}}}{3} - \dfrac{{{x^5}}}{{45}}} \right)} \right|_{ - \sqrt 3 }^{\sqrt 3 }} \right| $
$= 2\pi \left( {4\sqrt 3 - \sqrt 3 - \dfrac{{\sqrt 3 }}{5}} \right) = \dfrac{{28\pi \sqrt 3 }}{5}$
Vậy $V = \dfrac{{28\pi \sqrt 3 }}{5} = \dfrac{{a\pi \sqrt 3 }}{b} \Rightarrow \left\{ \begin{array}{l}a = 28\\b = 5\end{array} \right. \Rightarrow T = a + b = 28 + 5 = 33.$

