Gọi $V$ là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y = \sqrt x ,y = 0\) và $x = 4$ quanh trục $Ox$ . Đường thẳng \(x = a(0 < a < 4)\) cắt đồ thị hàm số \(y = \sqrt x \) tại $M$ (hình vẽ bên).

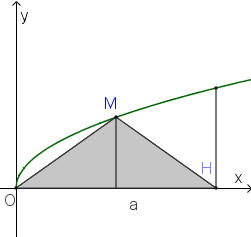
Gọi ${V_1}$ là thể tích khối tròn tạo thành khi quay quanh tam giác $OMH$ quanh trục $Ox$. Biết rằng \(V = 2{V_1}\) . Khi đó:

Cho hình phẳng \(\left( H \right)\) giới hạn bởi parabol \(y = a{x^2} + 1\,\,\,\left( {a > 0} \right)\), trục tung và đường thẳng \(x = 1\). Quay \(\left( H \right)\) quanh trục Ox được một khối tròn xoay có thể tích bằng \(\dfrac{{28}}{{15}}\pi \). Mệnh đề nào dưới đây đúng?

Gọi \(\left( H \right)\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = \sqrt {\dfrac{x}{{4 - {x^2}}}} \), trục Ox và đường thẳng \(x = 1\).  Khối tròn xoay sinh ra khi cho \(\left( H \right)\) quay quanh trục Ox có thể tích bằng

 Tìm thể tích \(V\) của vật tròn xoay sinh ra bởi đường tròn \({{x}^{2}}+{{\left( y-3 \right)}^{2}}=4\) khi quay quanh trục \(Ox.\)

Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y=\sqrt{x}\), cung tròn có phương trình \(y = \sqrt {6 - {x^2}} \) \(\left( -\,\sqrt{6}\le x\le \sqrt{6} \right)\) và trục hoành (phần tô đậm trong hình vẽ bên). Tính thể tích \(V\) của vật thể tròn xoay sinh bởi khi quay hình phẳng \(D\) quanh trục \(Ox\).

Trong mặt phẳng tọa độ Oxy, gọi \(\left( {{H_1}} \right)\) là hình phẳng giới hạn bởi các đường \(y = \frac{{{x^2}}}{4};\,\,y =  - \frac{{{x^2}}}{4};\,\,x =  - 4;\,\,x = 4\) và \(\left( {{H_2}} \right)\) là hình gồm tất cả các điểm \(\left( {x;y} \right)\) thỏa \({x^2} + {y^2} \le 16;\,\,{x^2} + {\left( {y - 2} \right)^2} \ge 4;\,\,{x^2} + {\left( {y + 2} \right)^2} \ge 4\)

Cho \(\left( {{H_1}} \right)\) và \(\left( {{H_2}} \right)\) quanh quanh trục Oy ta được các vật thể có thể tích là \({V_1},\,\,{V_2}\). Đẳng thức nào sau đây đúng ?

Cho nửa đường tròn đường kính \(AB=4\sqrt{5}\). Trên đó người ta vẽ một parabol có đỉnh trùng với tâm của nửa hình tròn, trục đối xứng là đường kính vuông góc với AB. Parabol cắt nửa đường tròn tại hia điểm cách nhau 4cm và khoảng cách từ hai điểm đó đến AB bằng nhau và bằng 4cm. Sau đó người ta cắt bỏ phần hình phẳng giới hạn bởi đường tròn và parabol (phần tô màu trong hình vẽ). Đem phần còn lại quay xung quanh trục AB. Thể tích của khối tròn xoay thu được bằng:

Cho hình phẳng giới hạn bởi đồ thị hàm số \(y=\frac{1}{x}\) và các đường thẳng \(y=0;\,\,x=1;\,\,x=4\). Tính thể tích V của khối tròn xoay sinh ra khi cho hình (H) quanh xung quanh trục Ox.