Gọi \(\left( {{D_1}} \right)\) là hình phẳng giới hạn bởi các đường \(y = 2\sqrt x ,\,\,y = 0\) và \(x = 2020,\) \(\left( {{D_2}} \right)\) là hình phẳng giới hạn bởi các đường \(y = \sqrt {3 x},\,\,y = 0\) và \(x = 2020.\) Gọi \({V_1},\,\,{V_2}\) lần lượt là thể tích khối tròn xoay tạo thành khi quay \(\left( {{D_1}} \right)\) và \(\left( {{D_2}} \right)\) xung quanh trục \(Ox.\) Tỉ số \(\dfrac{{{V_1}}}{{{V_2}}}\) bằng:
Ta có: \(\left( {{D_1}} \right)\) là hình phẳng giới hạn bởi các đường \(y = 2\sqrt x ,\,\,y = 0\) và \(x = 2020,\)
\( \Rightarrow {V_1} = \pi \int\limits_0^{2020} {\left| {{{\left( {2\sqrt x } \right)}^2}} \right|dx} \) \( = \pi \int\limits_0^{2020} {4xdx} = \left. {2\pi {x^2}} \right|_0^{2020}\) \( = 2\pi {.2020^2}.\)
\(\left( {{D_2}} \right)\) là hình phẳng giới hạn bởi các đường \(y = \sqrt {3x} ,\,\,y = 0\) và \(x = 2020\)
\( \Rightarrow {V_2} = \pi \int\limits_0^{2020} {\left| {{{\left( {\sqrt {3x} } \right)}^2}} \right|dx} \) \( = \pi \int\limits_0^{2020} {3xdx} = \left. {\frac{3}{2}\pi {x^2}} \right|_0^{2020}\) \( = \frac{3}{2}\pi {.2020^2}.\)
\(\Rightarrow \frac{{{V_1}}}{{{V_2}}} = \frac{{2\pi {{.2020}^2}}}{{\frac{3}{2}\pi {{.2020}^2}}} = \frac{4}{3}.\)
Tính thể tích hình xuyến do quay hình tròn có phương trình ${x^2} + {\left( {y - 2} \right)^2} = 1$ khi quanh trục $Ox.$
Xét $\left( C \right):{x^2} + {\left( {y - 2} \right)^2} = 1$ có tâm $I\left( {0;2} \right),$ bán kính $R = 1.$ Như vậy
Nửa $\left( C \right)$ trên ứng với $2 \le y \le 3$ có phương trình $y = {f_1}\left( x \right) = 2 + \sqrt {1 - {x^2}} $ với $x \in \left[ { - \,1;1} \right].$
Nửa $\left( C \right)$ dưới ứng với $1 \le y \le 2$ có phương trình $y = {f_2}\left( x \right) = 2 - \sqrt {1 - {x^2}} $ với $x \in \left[ { - \,1;1} \right].$
Khi đó, thể tích khối tròn xoay cần tính là
$V = \pi \int\limits_{ - \,1}^1 {\left[ {{{\left( {2 + \sqrt {1 - {x^2}} } \right)}^2} - {{\left( {2 - \sqrt {1 - {x^2}}} \right)}^2}} \right]\,{\rm{d}}x} = 8\pi \int\limits_{ - \,1}^1 {\sqrt {1 - {x^2}} \,{\rm{d}}x} .$
Đặt $x = \sin t \Leftrightarrow {\rm{d}}x = \cos t\,{\rm{d}}t$ và đổi cận $\left\{ \begin{array}{l}x = - \,1\, \Rightarrow \,t = - \dfrac{\pi }{2}\\x = 1\, \Rightarrow \,t = \dfrac{\pi }{2}\end{array} \right..$
Khi đó $V = 8\pi \int\limits_{ - \,\dfrac{\pi }{2}}^{\dfrac{\pi }{2}} {\sqrt {{{\cos }^2}t} .\cos t\,{\rm{d}}t} = 4\pi \int\limits_{ - \,\dfrac{\pi }{2}}^{\dfrac{\pi }{2}} {\left( {1 + \cos 2t} \right)\,{\rm{d}}t} = 4\pi \left. {\left( {t + \dfrac{1}{2}\sin 2t} \right)} \right|_{ - \,\dfrac{\pi }{2}}^{\dfrac{\pi }{2}} = 4{\pi ^2}.$
Cho hình phẳng \(\left( H \right)\) giới hạn bởi các đường \(y=\sqrt{x}\), \(y=-\,x\) và \(x=4.\) Thể tích của khối tròn xoay tạo thành khi quay hình \(\left( H \right)\) quanh trục hoành là \(V=\dfrac{a\pi }{b},\) với \(a,\,\,b>0\) và \(\dfrac{a}{b}\) là phân số tối giản. Tính tổng \(T=a+b.\)
Đáp án:
Đáp án:
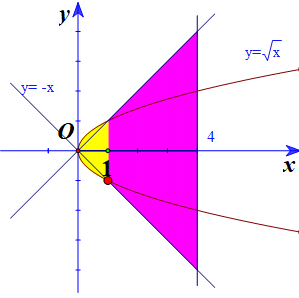
Hình trên là phần thiết diện của khối tròn xoay bị cắt bởi Oxy
Bước 1: Xét phương trình hoành độ giao điểm.
Phương trình hoành độ giao điểm của \(y=\sqrt{x},\,\,y=-\,x\) là \(\sqrt{x}=-\,x\Leftrightarrow x=0.\)
Bước 2: Tách tích phân ban đầu thành tích phân từ 0 đến 1 và từ 1 đến 4
Khi đó, thể tích cần tính là
\(\begin{array}{l}V = \pi \int\limits_0^1 {{{\left( {\sqrt x } \right)}^2}dx} + \pi \int\limits_1^4 {{{\left( { - x} \right)}^2}dx} \\ = \dfrac{\pi }{2} + 21\pi = \dfrac{{43\pi }}{2}\end{array}\)
=>$a+b=43+2=45$
Một thùng rượu có bán kính các đáy là \(30\;{\rm{cm}}\), thiết diện vuông góc với trục và cách đều hai đáy có bán kính là \(40\;{\rm{cm}}\), chiều cao thùng rượu là \(1\;{\rm{m}}\). Biết rằng mặt phẳng chứa trục và cắt mặt xung quanh thùng rượu là các đường parabol, hỏi thể tích của thùng rượu là bao nhiêu?

425,2 lít.
425,2 lít.
425,2 lít.
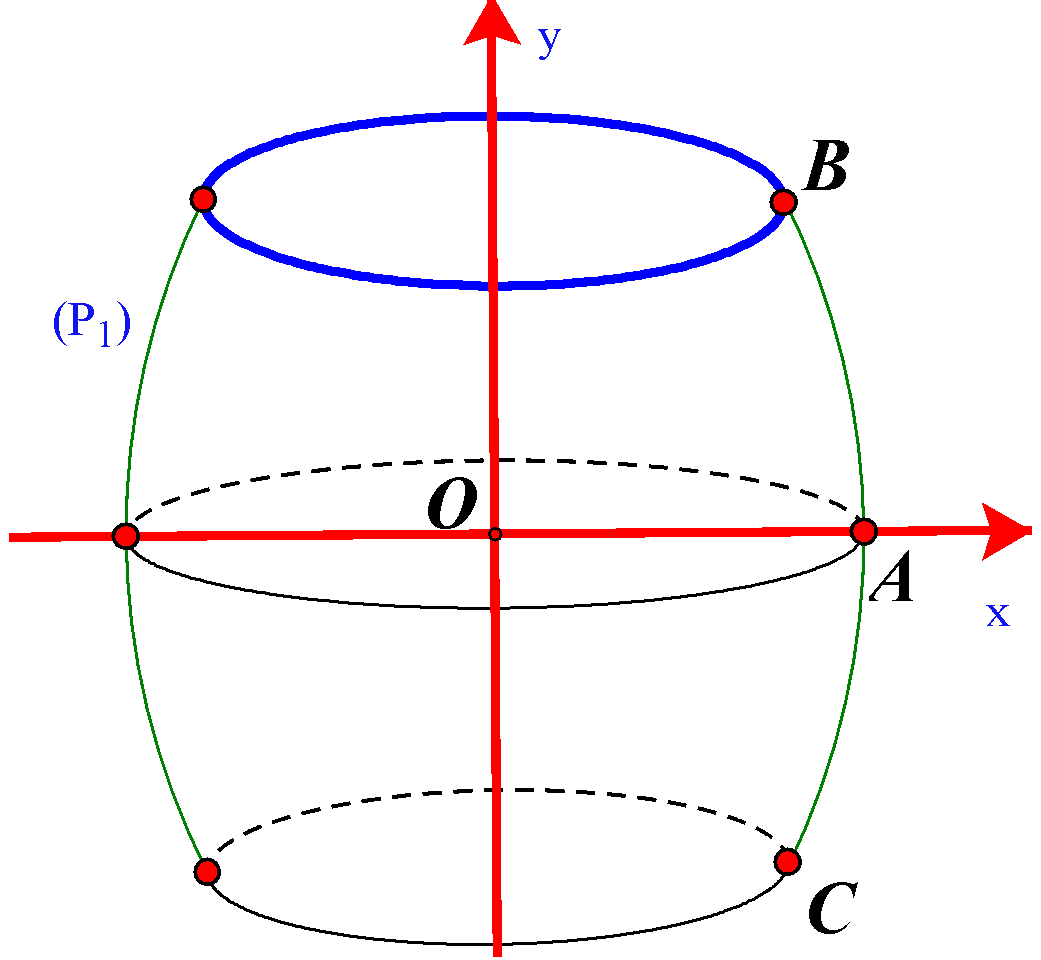
Bước 1: Đặt mặt cắt qua trục của thùng rượu lên hệ trục tọa độ Oxy. Gọi \((P):x = a{y^2} + by + c\), tìm (P).
Đơn vị tính là dm.
Gọi \((P):x = a{y^2} + by + c\) qua \(A(4;0),B(3;5),C(3; - 5)\).
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = - \dfrac{1}{{25}}}\\{b = 0}\\{c = 4}\end{array}} \right.\)\( \Rightarrow (P):x = - \dfrac{1}{{25}}{y^2} + 4\)
Bước 2: Tính thể tích thùng rượu
Thể tích của thùng rượu là
\(V = \pi \int_{ - 5}^5 {{{\left( { - \dfrac{1}{{25}}{y^2} + 4} \right)}^2}} dy\)\( \approx 425,2\left( {d{m^3}} \right) = 425,2(l)\)
Cho \(\left( H \right)\) là hình phẳng giới hạn bởi các đường \(y = \sqrt x \) và \(y = {x^2}.\) Thể tích của khối tròn xoay tạo thành khi quay hình \(\left( H \right)\) quanh trục \(Ox\) bằng
ĐK: \(x \ge 0.\)
Xét phương trình hoành độ giao điểm của hai đường thẳng \(y = \sqrt x \) và \(y = {x^2}\):
\(\begin{array}{l}\sqrt x = {x^2} \Leftrightarrow \sqrt x \left( {x\sqrt x - 1} \right) = 0\\ \Leftrightarrow \sqrt x \left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\\sqrt x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\end{array}\)
Vậy thể tích khối tròn xoay tạo thành là \(V = \pi \int\limits_0^1 {\left| {{{\left( {\sqrt x } \right)}^2} - {{\left( {{x^2}} \right)}^2}} \right|dx} = \dfrac{{3\pi }}{{10}}\).

