Tích phân (Khái niệm và tính chất)

Ta có \(f\left( x \right)\) là 1  nguyên hàm của hàm số \(f'\left( x \right)\) nên \(I = \int\limits_0^1 {f'\left( x \right){\rm{d}}x}  = f\left( 1 \right) - f\left( 0 \right) = 2\).

\(\int\limits_1^4 {\left[ {f\left( x \right) - g\left( x \right)} \right]dx}  = \int\limits_1^4 {f\left( x \right)dx}  - \int\limits_1^4 {g\left( x \right)dx} \) \( = 3 - \left( { - 2} \right) = 5\).

Ta có: \(\int\limits_0^1 {\left[ {f\left( x \right) - 2g\left( x \right)} \right]dx}  = \int\limits_0^1 {f\left( x \right)dx}  - 2\int\limits_0^1 {g\left( x \right)dx}  = 2 - 2.5 =  - 8\)

Ta có \(\int\limits_0^3 {3f\left( x \right)dx}  = 3\int\limits_0^3 {f\left( x \right)dx}  = 3.4 = 12\).

Ta có: \(\int\limits_0^2 {\left[ {2f\left( x \right) - 1} \right]dx = 2\int\limits_0^2 {f\left( x \right)dx - \int\limits_0^2 {1dx = 2.4 - 2 = 6} } } \)

Ta có: \(\int\limits_1^4 {\left[ {f\left( x \right) - g\left( x \right)} \right]dx}  = \)\(\int\limits_1^4 {f\left( x \right)dx}  - \int\limits_1^4 {g\left( x \right)dx = 6 - \left( { - 5} \right) = 11} \)

Ta có: \(I = \int\limits_0^{ - 1} {f\left( x \right)dx + 2\int\limits_0^2 {f\left( x \right)dx = F\left( { - 1} \right) - F\left( 0 \right) + 2F\left( 2 \right) - 2F\left( 0 \right)} } \)

Do đó \(I = F\left( { - 1} \right) + 2F\left( 2 \right) - 3F\left( 0 \right) = F\left( { - 1} \right) + 2F\left( 2 \right) - 6 \Rightarrow F\left( { - 1} \right) + 2F\left( 2 \right) = I + 6\)

Mà \(\int\limits_0^{ - 1} {f\left( x \right)dx =  - \int\limits_{ - 1}^0 {\left( {3{x^2} + 1} \right)dx =  - 2} } \) và \(2\int\limits_0^2 {f\left( x \right)dx = } 2\left( {\int\limits_0^1 {\left( {3{x^2} + 1} \right)dx + \int\limits_1^2 {\left( {2x + 2} \right)dx} } } \right) = 14\)

Suy ra \(I =  - 2 + 14 = 12\)

Do đó \(F\left( { - 1} \right) + 2F\left( 2 \right) = 12 + 6 = 18\).

Bước 1: Trên khoảng \((1; + \infty )\) tính hằng số \({C_1}\)

+) Trên khoảng \((1; + \infty )\) ta có

\(\int {{f^\prime }} (x)dx = \int {\dfrac{1}{{x - 1}}} dx = \ln (x - 1) + {C_1} \Rightarrow f(x) = \ln (x - 1) + {C_1}\)

Mà \(f(2) = 2018 \Rightarrow {C_1} = 2018\).

Bước 2: Trên khoảng \(( - \infty ;1)\) tính hằng số \({C_2}\)

+) Trên khoảng \(( - \infty ;1)\) ta có

\(\int {{f^\prime }} (x)dx = \int {\dfrac{1}{{x - 1}}} dx = \ln (1 - x) + {C_2} \Rightarrow f(x) = \ln (1 - x) + {C_2}.\)

Mà \(f(0) = 2017 \Rightarrow {C_2} = 2017\).

Bước 3: Tính \(f(3) - f( - 1)\)

Vậy \(f(x) = \left\{ {\begin{array}{*{20}{l}}{\ln (x - 1) + 2018}&{{\rm{ khi }}}&{x > 1}\\{\ln (1 - x) + 2017}&{{\rm{ khi }}}&{x < 1}\end{array}.} \right.\) Suy ra \(f(3) - f( - 1) = 1.\)

Sử dụng các tính chất của tích phân: \(\int\limits_a^b {\left[ {f\left( x \right) \pm g\left( x \right)} \right]dx}  = \int\limits_a^b {f\left( x \right)dx}  \pm \int\limits_a^b {g\left( x \right)dx} .\)

\(\int\limits_1^5 {f\left( x \right)dx}  = \int\limits_1^2 {f\left( x \right)dx}  + \int\limits_2^5 {f\left( x \right)dx}  = 3 + \left( { - 4} \right) =  - 1\)

Ta có: \(\int\limits_0^2 {\left[ {2f\left( x \right) - 1} \right]dx}  = 2\int\limits_0^2 {f\left( x \right)dx}  - \int\limits_0^2 {1dx} \) \( = 2.5 - \left. x \right|_0^2 = 10 - \left( {2 - 0} \right) = 8\).

Bước 1: \(1 + f(x) = f(x)f(1 - x) + f(x)\)

Ta có \(1 + f(x) = f(x)f(1 - x) + f(x)\)\( \Rightarrow \dfrac{{f\left( x \right)}}{{1 + f\left( x \right)}} = \dfrac{1}{{f\left( {1 - x} \right) + 1}}\)

Bước 2: Xét tích phân \(I = \int_0^1 {\dfrac{{dx}}{{1 + f(x)}}} \)

Xét \(I = \int_0^1 {\dfrac{{dx}}{{1 + f(x)}}} \). Đặt \(t = 1 - x \Leftrightarrow x = 1 - t \Rightarrow dx =  - dt\).

Đổi cận \(x = 0 \Rightarrow t = 1;x = 1 \Rightarrow t = 0\).

Khi đó, \(I =  - \int_1^0 {\dfrac{{{\rm{d}}t}}{{1 + f(1 - t)}}}  = \int_0^1 {\dfrac{{{\rm{d}}t}}{{1 + f(1 - t)}}}  = \)\( = \int\limits_0^1 {\dfrac{{dx}}{{1 + f\left( {1 - x} \right)}}}  = \int\limits_0^1 {\dfrac{{f\left( x \right)dx}}{{1 + f\left( x \right)}}} \)

Mặt khác, \(\int_0^1 {\dfrac{{dx}}{{1 + f(x)}}}  + \int_0^1 {\dfrac{{f(x)dx}}{{1 + f(x)}}} \)\( = \int\limits_0^1 {\dfrac{{1 + f\left( x \right)}}{{1 + f\left( x \right)}}dx = \int\limits_0^1 {dx}  = 1} \) hay \(2I = 1\).

Vậy \(I = \dfrac{1}{2}\).

Cách 1: Không đi tìm hàm \(F\left( x \right)\).

Ta có:

\(\begin{array}{l}P = F\left( { - 1} \right) + 2F\left( 2 \right)\\\,\,\,\,\, = \left[ {F\left( { - 1} \right) - F\left( 0 \right)} \right] + 2\left[ {F\left( 2 \right) - F\left( 0 \right)} \right] + 3F\left( 0 \right)\\\,\,\,\,\,\, = \int\limits_0^{ - 1} {f\left( x \right)dx}  + 2\int\limits_0^2 {f\left( x \right)dx}  + 3F\left( 0 \right)\end{array}\)

(Hàm số \(F\left( x \right)\) là hàm số thay đổi công thức tại \(x = 1\), nhưng liên tục tại \(x = 1\), nên việc ta khẳng định \(\int\limits_0^2 {f\left( x \right)dx}  = F\left( 2 \right) - F\left( 0 \right)\) là hoàn toàn chặt chẽ bản chất và việc phân đoạn tích phân vẫn đúng).

\(\begin{array}{l} \Rightarrow P = \int\limits_0^{ - 1} {f\left( x \right)dx}  + 2\left[ {\int\limits_0^1 {f\left( x \right)dx}  + \int\limits_1^2 {f\left( x \right)dx} } \right] + 3.2\\\,\,\,\,\,\,\,\,\,\,\, = \int\limits_0^{ - 1} {\left( {3{x^2} + 4} \right)dx}  + 2\left[ {\int\limits_0^1 {\left( {3{x^2} + 4} \right)dx}  + \int\limits_1^2 {\left( {2x + 5} \right)dx} } \right] + 6\\\,\,\,\,\,\,\,\,\,\,\, = 27\end{array}\)

Cách 2: Tìm hàm \(F\left( x \right)\).

\(f\left( x \right) = \left\{ \begin{array}{l}2x + 5\\3{x^2} + 4\end{array} \right. \Rightarrow F\left( x \right) = \int {f\left( x \right)dx}  = \left\{ \begin{array}{l}{x^2} + 5x + {C_1}\,\,khi\,\,x \ge 1\\{x^3} + 4x + {C_2}\,\,khi\,\,x < 1\end{array} \right.\).

+ Vì \(F\left( 0 \right) = 2 \Rightarrow {0^3} + 4.0 + {C_2} = 2 \Leftrightarrow {C_2} = 2\).

+ Theo giả thiết, \(F\left( x \right)\) là hàm số tồn tại đạo hàm trên \(\mathbb{R}\).

\( \Rightarrow F\left( x \right)\) tồn tại đạo hàm tại \(x = 1 \Rightarrow F\left( x \right)\) liên tục tại \(x = 1\).

\( \Rightarrow F\left( {{1^ + }} \right) = F\left( {{1^ - }} \right) = F\left( 1 \right) \Rightarrow 1 + 5 + {C_1} = 1 + 4 + {C_2}\) \( \Rightarrow {C_1} =  - 1 + {C_2} = 1\).

\(\begin{array}{l} \Rightarrow F\left( x \right) = \left\{ \begin{array}{l}{x^2} + 5x + 1\,\,khi\,\,x \ge 1\\{x^3} + 4x + 2\,\,khi\,\,x < 1\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}F\left( { - 1} \right) = {\left( { - 1} \right)^3} + 4.\left( { - 1} \right) + 2 =  - 3\\F\left( 2 \right) = {2^2} + 5.2 + 1 = 15\end{array} \right.\\ \Rightarrow P = F\left( { - 1} \right) + 2F\left( 2 \right) =  - 3 + 2.15 = 27\end{array}\)

\(2\int\limits_3^4 {f\left( x \right)dx}  = 2.5 = 10\).

\(\begin{array}{l}\,\,\,\,\,\,\,\int\limits_0^3 {\left[ {4f\left( x \right) - 3{x^2}} \right]dx}  = 5\\ \Leftrightarrow 4\int\limits_0^3 {f\left( x \right)dx}  - \int\limits_0^3 {3{x^2}dx}  = 5\\ \Leftrightarrow 4\int\limits_0^3 {f\left( x \right)dx}  - \left. {{x^3}} \right|_0^3 = 5\\ \Leftrightarrow 4\int\limits_0^3 {f\left( x \right)dx}  - 27 = 5\\ \Leftrightarrow \int\limits_0^3 {f\left( x \right)dx}  = 8\end{array}\)

Ta có: \(\int\limits_0^3 {2f\left( x \right)dx}  = 2\int\limits_0^3 {f\left( x \right)dx}  = 2.3 = 6\)

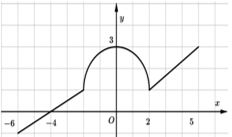
\(y=f(x)=\left\{ \begin{align}  \frac{x+4}{2},\,\,x<-2 \\  \sqrt{4-{{x}^{2}}}+1,\,\,-2\le x\le 2 \\  \frac{2x-1}{3},\,\,x>2 \\ \end{align} \right.\,\,\)

\(\begin{align}  I=\int\limits_{-6}^{5}{\left[ f(x)+2 \right]dx}=\int\limits_{-6}^{5}{f(x)dx}+\int\limits_{-6}^{5}{2dx}=\int\limits_{-6}^{-2}{\frac{x+4}{2}dx}+\int\limits_{-2}^{2}{\left( \sqrt{4-{{x}^{2}}}+1 \right)dx}+\int\limits_{2}^{5}{\frac{2x-1}{3}dx}+\int\limits_{-6}^{5}{2dx} \\  =\int\limits_{-6}^{-2}{\frac{x+4}{2}dx}+\int\limits_{-2}^{2}{\sqrt{4-{{x}^{2}}}dx}+\int\limits_{-2}^{2}{dx}+\int\limits_{2}^{5}{\frac{2x-1}{3}dx}+\int\limits_{-6}^{5}{2dx} \\  =0+{{I}_{1}}+4+6+22={{I}_{1}}+32 \\ \end{align}\)

Trong đó \({{I}_{1}}=\int\limits_{-2}^{2}{\sqrt{4-{{x}^{2}}}dx}\), đặt \(x=2\sin t\Rightarrow dx=2\cos tdt\), đổi cận \(x=-2\to t=-\frac{\pi }{2};\,\,x=2\to t=\frac{\pi }{2}\)

 \(\Rightarrow {{I}_{1}}=\int\limits_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{\sqrt{4-4{{\sin }^{2}}t}.2\cos tdt}=4\int\limits_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{{{\cos }^{2}}tdt}=2\int\limits_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{\left( \cos 2t+1 \right)dt}=\left. \left( \sin 2t+2t \right) \right|_{-\frac{\pi }{2}}^{\frac{\pi }{2}}=2\pi \)

 \(\Rightarrow I=2\pi +32\).

Ta có: \(\int\limits_2^3 {2f\left( x \right)dx}  = 2\int\limits_2^3 {f\left( x \right)dx}  = 2.6 = 12.\)

\(\begin{align}  & \int\limits_{1}^{3}{\left[ f\left( x \right)+3g\left( x \right) \right]dx=10}\Leftrightarrow \int\limits_{1}^{3}{f(x)dx+3\int\limits_{1}^{3}{g\left( x \right)dx=10}} \\ & \int\limits_{1}^{3}{\left[ 2f\left( x \right)-g\left( x \right) \right]dx}=6\Leftrightarrow 2\int\limits_{1}^{3}{f\left( x \right)dx}-\int\limits_{1}^{3}{g\left( x \right)dx}=6 \\ \end{align}\)

\( \Rightarrow \left\{ \begin{align}  & \int\limits_{1}^{3}{f\left( x \right)dx=}4 \\ & \int\limits_{1}^{3}{g\left( x \right)dx=2} \\ \end{align} \right.\,\,\,\,\,\,\) \(\Rightarrow \begin{align} \int\limits_{1}^{3}{\left[ f\left( x \right)+g\left( x \right) \right]dx}=\int\limits_{1}^{3}{f\left( x \right)dx}+\int\limits_{1}^{3}{g\left( x \right)dx=4+2=6} \\ \end{align}\)

Gọi \(G\left( t \right)\) là một nguyên hàm của hàm số \(g\left( t \right)={{t}^{2}}\,\,\Rightarrow \,\,G\left( t \right)=\frac{{{t}^{3}}}{3}.\)

Ta có \(\int\limits_{0}^{f\left( x \right)}{{{t}^{2}}\,\text{d}t}=x.\cos \pi x\Leftrightarrow \left. \frac{{{t}^{3}}}{3} \right|_{0}^{f\left( x \right)}\Leftrightarrow \frac{{{f}^{3}}\left( x \right)}{3}=x\cos \pi x\)   

\(\Leftrightarrow {{f}^{3}}\left( x \right)=3x\cos \pi x\Leftrightarrow f\left( x \right)=\sqrt[3]{3x\cos \pi x}. \ \ \left( * \right)\)   

Thay \(x=4\) vào đẳng thức \(\left( * \right),\) ta được \(f\left( 4 \right)=\sqrt[3]{3.4.\cos 4\pi }=\sqrt[3]{12}.\)